model.eval 至关重要！！！！model.eval()是否开启 BN 和 Dropout 的不同

之前写过一个项目，eval的时候很正常，但是一infer就有问题，多次排查发现，原来就是只缺一个

model.eval()
1

哇，重大教训，我debug好久，在小姑娘面前翻车… 🤣🤣🤣

在文档中 nn.Module (torch) 或者 nn.Layer (Paddle) 的 eval 都是说会影响 Dropout 和 BatchNorm

本文来看一下 eval 对 dropout 和 BatchNorm 做了什么

1. Dropout

import paddle
import paddle.nn as nn

model = nn.Dropout(0.9)
model.train()
inp = paddle.rand([3, 4])
out = model(inp)
1
2
3
4
5
6
7

>>> inp
Tensor(shape=[3, 4], dtype=float32, place=Place(gpu:0), stop_gradient=True,
       [[0.62465787, 0.75934911, 0.22212228, 0.46498537],
        [0.52518481, 0.94535673, 0.77799159, 0.50506479],
        [0.26053512, 0.26007101, 0.17834763, 0.70845836]])
        
>>> out 
Tensor(shape=[3, 4], dtype=float32, place=Place(gpu:0), stop_gradient=True,
       [[0.        , 0.        , 0.        , 0.        ],
        [0.        , 0.        , 0.        , 0.        ],
        [0.        , 0.        , 0.        , 7.08458233]])
1
2
3
4
5
6
7
8
9
10
11

但是如果加上 model.eval

import paddle
import paddle.nn as nn

model = nn.Dropout(0.9)
model.eval()
inp = paddle.rand([3, 4])
out = model(inp)
1
2
3
4
5
6
7

>>> inp
Tensor(shape=[3, 4], dtype=float32, place=Place(gpu:0), stop_gradient=True,
       [[0.85406083, 0.30777919, 0.84194952, 0.31621146],
        [0.19795220, 0.84470266, 0.64288461, 0.28012937],
        [0.76796150, 0.28145868, 0.44665241, 0.64438581]])
        
>>> out 
Tensor(shape=[3, 4], dtype=float32, place=Place(gpu:0), stop_gradient=True,
       [[0.85406083, 0.30777919, 0.84194952, 0.31621146],
        [0.19795220, 0.84470266, 0.64288461, 0.28012937],
        [0.76796150, 0.28145868, 0.44665241, 0.64438581]])
1
2
3
4
5
6
7
8
9
10
11

2. BatchNorm

如果 model 没有设置 .eval，则在 infer 中大概率有问题，因为 infer 一般 batch_size 为1，导致推理时的偏差较大，来，接下来看看到底是怎么个偏差较大

这里专门用 mnist 来做个例子，用Paddle实现，torch差不多

数据集加载：

import paddle
import paddle.nn as nn
import paddle.vision.transforms as T
from paddle.vision.datasets import MNIST
from paddle.io import DataLoader


transform = T.Compose(
    [
        T.ToTensor(),
        T.Normalize(
            mean=[127.5],
            std=[127.5],
        ),
    ]
)

train_mnist = MNIST(
    mode="train",
    transform=transform,
    backend="cv2",
)
test_mnist  = MNIST(
    mode="test",
    transform=transform,
    backend="cv2",
)

train_loader = DataLoader(
    dataset=train_mnist,
    shuffle=True,
    num_workers=8,
    batch_size=256,
)
test_loader = DataLoader(
    dataset=test_mnist,
    shuffle=False,
    num_workers=8,
    batch_size=256,
)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41

模型定义：（也可通过本demo学习BN中的 moving_mean 和 moving_variance 是如何计算的）

class Model(nn.Layer):
    def __init__(self, hidden_num=32, out_num=10):
        super().__init__()
        self.fc1 = nn.Linear(28*28, hidden_num)
        self.bn  = nn.BatchNorm(hidden_num)
        self.fc2 = nn.Linear(hidden_num, out_num)
        self.softmax = nn.Softmax()
    def forward(self, inputs, **kwargs):
        x = inputs.flatten(1)
        x = self.fc1(x)
        
        print("========= bn之前存的数据: =========")
        print(self.bn._mean, self.bn._variance)
        print()
        
        x_mean = x.mean(0)
        # x_variance = paddle.var(x, 0)
        x_variance = ((x - x_mean)*(x - x_mean)).mean(0)
        
        print("========= 当前 Batch 的数据: =========")
        print(x_mean, x_variance)
        print()
        
        bn_new_mean = self.bn._mean * self.bn._momentum + x_mean * (1-self.bn._momentum)
        bn_new_var  = self.bn._variance * self.bn._momentum + x_variance * (1-self.bn._momentum)
        print("========= 手动计算的新数据数据: =========")
        print(bn_new_mean, bn_new_var)
        print()
        
        x = self.bn(x)
        print("========= bn计算之后的新数据: =========")
        print(self.bn._mean, self.bn._variance)
        print()
        
        # x = self.dropout(x)
        x = self.fc2(x)
        x = self.softmax(x)
        return x
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38

训练开始：

model = Model()
model.train()
for img, label in train_loader:
    label = nn.functional.one_hot(label.flatten(), 10)
    out = model(img)
    break
1
2
3
4
5
6

来看下最后的输出：

========= bn之前存的数据: =========
Parameter containing:
Tensor(shape=[32], dtype=float32, place=Place(gpu:0), stop_gradient=True,
       [0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
        0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.]) Parameter containing:
Tensor(shape=[32], dtype=float32, place=Place(gpu:0), stop_gradient=True,
       [1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.,
        1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.])

========= 当前 Batch 的数据: =========
Tensor(shape=[32], dtype=float32, place=Place(gpu:0), stop_gradient=False,
       [-0.38882941,  0.03430356,  0.72941995,  0.88257772,  0.59287441,
         1.43031311,  1.16276920, -0.10491234, -0.93039852,  0.42681891,
         1.14838040, -0.21730696, -0.54693860, -0.14556082, -1.01294327,
        -0.71115893,  1.10771430, -0.77535808,  0.39560708, -0.68615019,
         1.51775694, -0.47886604, -0.14928204,  0.50894970,  1.76031160,
         0.50432783,  0.19052365, -2.01953459,  1.84687483, -0.70989704,
        -1.44391048,  1.64701092]) Tensor(shape=[32], dtype=float32, place=Place(gpu:0), stop_gradient=False,
       [0.58479834, 0.99659586, 0.33979574, 0.48517889, 0.65143955, 0.56042129,
        0.48198137, 0.41009885, 0.56537294, 0.50146306, 0.37284675, 0.24294424,
        0.71886718, 0.40560260, 0.49942270, 0.51505977, 0.71436852, 0.46243513,
        0.44024459, 0.76668155, 0.48029205, 0.57720137, 0.33403489, 0.41284043,
        0.37509984, 0.62300909, 0.53987831, 0.60129762, 0.55340236, 0.34260243,
        0.53284788, 0.49520931])

========= 手动计算的新数据数据: =========
Tensor(shape=[32], dtype=float32, place=Place(gpu:0), stop_gradient=False,
       [-0.03888294,  0.00343036,  0.07294200,  0.08825777,  0.05928744,
         0.14303131,  0.11627692, -0.01049123, -0.09303986,  0.04268189,
         0.11483804, -0.02173070, -0.05469386, -0.01455608, -0.10129433,
        -0.07111590,  0.11077143, -0.07753581,  0.03956071, -0.06861502,
         0.15177570, -0.04788661, -0.01492820,  0.05089497,  0.17603116,
         0.05043278,  0.01905237, -0.20195346,  0.18468748, -0.07098971,
        -0.14439104,  0.16470109]) Tensor(shape=[32], dtype=float32, place=Place(gpu:0), stop_gradient=False,
       [0.95847982, 0.99965954, 0.93397957, 0.94851786, 0.96514392, 0.95604211,
        0.94819814, 0.94100988, 0.95653725, 0.95014626, 0.93728465, 0.92429441,
        0.97188669, 0.94056022, 0.94994223, 0.95150596, 0.97143686, 0.94624346,
        0.94402444, 0.97666812, 0.94802916, 0.95772010, 0.93340349, 0.94128400,
        0.93750995, 0.96230090, 0.95398784, 0.96012974, 0.95534021, 0.93426025,
        0.95328474, 0.94952089])

========= bn计算之后的新数据: =========
Parameter containing:
Tensor(shape=[32], dtype=float32, place=Place(gpu:0), stop_gradient=True,
       [-0.03888295,  0.00343036,  0.07294201,  0.08825779,  0.05928745,
         0.14303134,  0.11627695, -0.01049124, -0.09303988,  0.04268190,
         0.11483806, -0.02173070, -0.05469387, -0.01455608, -0.10129435,
        -0.07111591,  0.11077145, -0.07753582,  0.03956072, -0.06861503,
         0.15177573, -0.04788661, -0.01492821,  0.05089498,  0.17603120,
         0.05043279,  0.01905237, -0.20195350,  0.18468753, -0.07098972,
        -0.14439109,  0.16470113]) Parameter containing:
Tensor(shape=[32], dtype=float32, place=Place(gpu:0), stop_gradient=True,
       [0.95870918, 1.00005043, 0.93411279, 0.94870818, 0.96539938, 0.95626187,
        0.94838715, 0.94117069, 0.95675898, 0.95034295, 0.93743086, 0.92438966,
        0.97216862, 0.94071931, 0.95013809, 0.95170796, 0.97171700, 0.94642484,
        0.94419706, 0.97696882, 0.94821757, 0.95794648, 0.93353444, 0.94144595,
        0.93765706, 0.96254522, 0.95419955, 0.96036553, 0.95555723, 0.93439460,
        0.95349371, 0.94971514])
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58

可以看到咱手动计算的 moving_mean 和 moving_variance 和 BN 内部计算的大差不差

OK, 接下里看看BN .train 和 .eval 有啥区别

paddle.seed(1107)
model = nn.BatchNorm(4)
model.eval()
inp = paddle.rand([2, 4])
out = model(inp)
1
2
3
4
5

>>> out
Tensor(shape=[2, 4], dtype=float32, place=Place(gpu:0), stop_gradient=False,
       [[0.33660540, 0.05333305, 0.47220078, 0.21046987],
        [0.03869555, 0.67438763, 0.12688087, 0.62906295]])
1
2
3
4

>>> inp
Tensor(shape=[2, 4], dtype=float32, place=Place(gpu:0), stop_gradient=False,
       [[0.33660540, 0.05333305, 0.47220078, 0.21046987],
        [0.03869555, 0.67438763, 0.12688087, 0.62906295]])
1
2
3
4

eval 情况下，BN模型直接用已经记录的 mean 和 var 来进行BN操作，而不是用那个滑动平均值去计算
而默认情况下，BN模型职工的 mean 和 var 是多少呢?

来看下源代码：

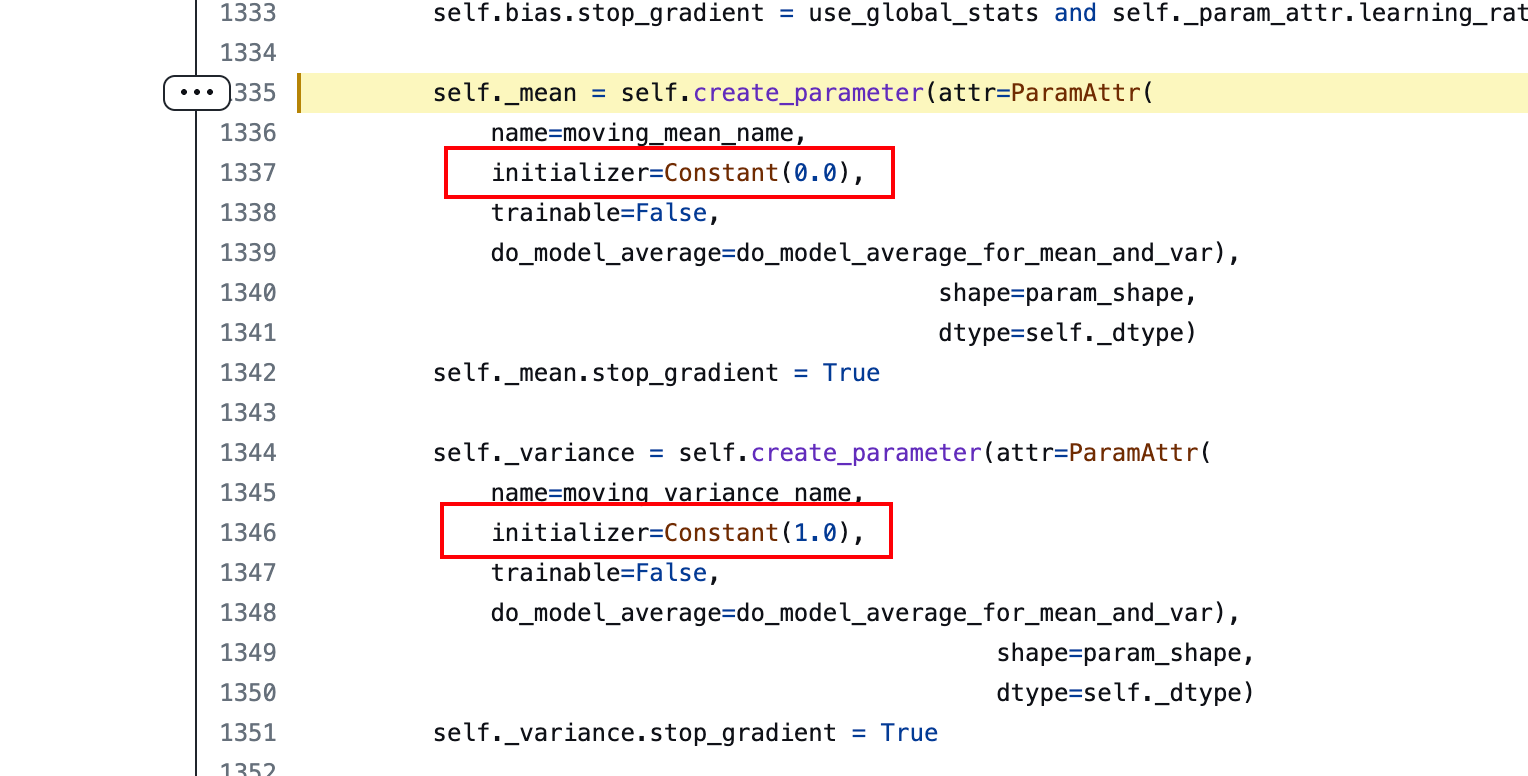
默认情况下mean都是0，var都是1，

而在.train()训练情况下，会计算原有值和数据分布值的一个加权平均

$$\begin{gathered} moving\_mean=moving\_mean\ast momentum+{\mu }_{\beta }\ast (1.-momentum)//globalmean \\ moving\_variance=moving\_variance\ast momentum+{\sigma }_{\beta }^2\ast (1.-momentum)//globalvariance \end{gathered}$$

paddle.seed(1107)
model = nn.BatchNorm(4)
model.train()
inp = paddle.rand([2, 4])
out = model(inp)
1
2
3
4
5

>>> out
Tensor(shape=[2, 4], dtype=float32, place=Place(gpu:0), stop_gradient=False,
       [[ 0.99977475, -0.99994820,  0.99983233, -0.99988586],
        [-0.99977475,  0.99994814, -0.99983233,  0.99988598]])
1
2
3
4

>>> inp
Tensor(shape=[2, 4], dtype=float32, place=Place(gpu:0), stop_gradient=False,
       [[0.33660540, 0.05333305, 0.47220078, 0.21046987],
        [0.03869555, 0.67438763, 0.12688087, 0.62906295]])
1
2
3
4

接下来手动计算一下看看，这是BN中原来的 mean 和 var：

>>> model._mean, model._variance
(Parameter containing:
 Tensor(shape=[4], dtype=float32, place=Place(gpu:0), stop_gradient=True,
        [0., 0., 0., 0.]),
        
 Parameter containing:
 Tensor(shape=[4], dtype=float32, place=Place(gpu:0), stop_gradient=True,
        [1., 1., 1., 1.]))
1
2
3
4
5
6
7
8

接下来计算一下数据的 mean 和 var:

>>> inp_mean = inp.mean(0)
>>> inp_mean
Tensor(shape=[4], dtype=float32, place=Place(gpu:0), stop_gradient=True,
       [0.18765143, 0.36386219, 0.29954234, 0.41976851])
       
>>> inp_var = ((inp - inp_mean) * (inp - inp_mean)).mean(0)
>>> inp_var
Tensor(shape=[4], dtype=float32, place=Place(gpu:0), stop_gradient=True,
       [0.02218779, 0.09642817, 0.02981176, 0.04380548])
1
2
3
4
5
6
7
8
9

手动计算一下以上二者的加权平均，这里用BN的默认值 momentum = 0.9 来计算

>>> my_bn_mean = inp_mean * 0.1 + 0 * 0.9
>>> my_bn_var = inp_var * 0.1 + 1 * 0.9
>>> my_bn_mean, my_bn_var

(Tensor(shape=[4], dtype=float32, place=Place(gpu:0), stop_gradient=True,
        [0.01876514, 0.03638622, 0.02995423, 0.04197685]),
        
 Tensor(shape=[4], dtype=float32, place=Place(gpu:0), stop_gradient=True,
        [0.90221876, 0.90964282, 0.90298116, 0.90438050]))
1
2
3
4
5
6
7
8
9

接下来打印一下bn模型计算计算之后的结果：

>>> model._mean, model._variance
(Parameter containing:
 Tensor(shape=[4], dtype=float32, place=Place(gpu:0), stop_gradient=True,
        [0.01876515, 0.03638623, 0.02995424, 0.04197686]),
        
 Parameter containing:
 Tensor(shape=[4], dtype=float32, place=Place(gpu:0), stop_gradient=True,
        [0.90443754, 0.91928560, 0.90596235, 0.90876108]))
1
2
3
4
5
6
7
8

以上结果大差不差，主要是在计算时还有一个 $ϵ=10^{-5}$ 来防止除0错误：
$$\begin{gathered} \widehat{x_i}\leftarrow \frac{x_i-{\mu }_{\beta }}{\sqrt{{\sigma }_{\beta }^2+ϵ}}//normalize \\ {y}_i\leftarrow \gamma \widehat{x_i}+\beta //scaleandshift \end{gathered}$$

eval开启后，BN不再计算和数据分布有关的加权平均值，而是直接用已有的值mean 和 var 进行计算

所以如果在infer过程中，bs=1，会极大的扰动BN中的_mean 和 _var值 导致模型预测出错

3. 总结

综上，infer 时，一定要开启 model.eval()