-
Surge:分子生成最前沿
这篇文章简要介绍分子生成程序
Surge的工作原理。Surge是当下最好的开源的分子生成程序,枚举百万量级分子仅需要0.1秒左右。文献前言
分子生成一直以来是化学信息学的研究热点。一个完备的分子数据库是开展分子虚拟筛选和探索分子构型空间的基础设施。该领域最早可以追溯到1960年代,NASA为探索火星生命开启了
Mariner项目,其中一个子任务是基于海量的质谱数据分析火星上可能存在的有机小分子,就此诞生了第一款分子生成程序DENDRAL。这款程序通过将经典的小分子结构排列组合,拼接形成大分子结构,此外能够剔除部分不合理的分子构型。与之类似的另一款程序ASSEMBLE也是采用类似的策略。事实上,这一阶段已经涉及到图论、排列组合等数学原理了。后来的MASS, SMOG, COCON, LSD, MOLGEN, GENG大都应用了数学原理,其中MOLGEN一直以来都是该领域的佼佼者,发展至今,MOLGEN 5.0是最快、完备性和可靠性最高的程序。然而,MOLGEN 5.0是闭源的商业软件,一定程度上阻碍了部分想要从业的有志之士。因此,构建开源的分子生成程序的呼声越来越高,
Surge就在这样的环境下应运而生。22年4月发表,一作是开发了图同构领域中Nauty程序的Brendan D. McKay。这位老爷子1980年博士毕业,算起来今年已经70岁左右了,还在亲手写程序,着实让人钦佩。废话不多说,Surge程序表现怎么样呢?下图是
Surge和MOLGEN的对比: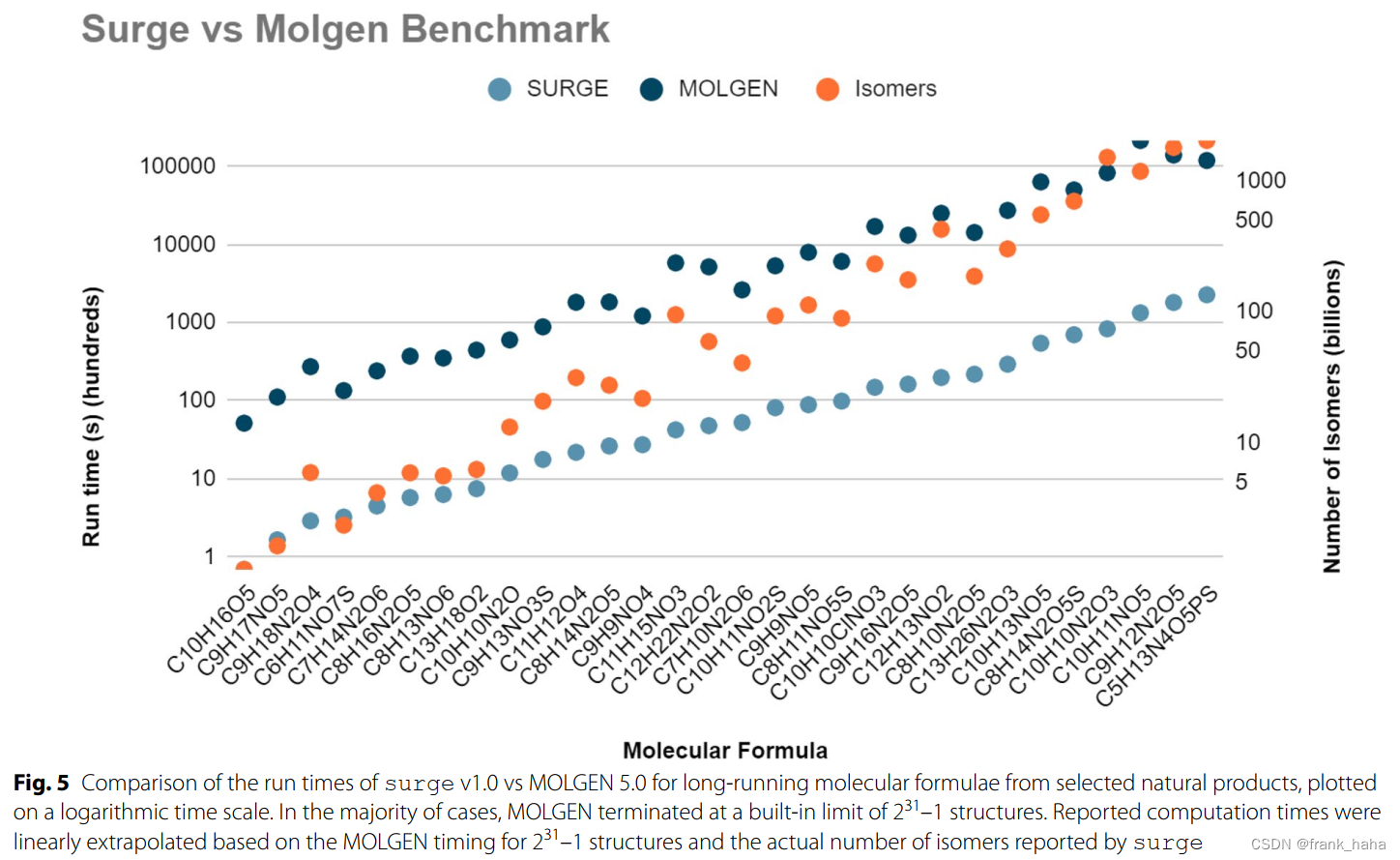
MOLGEN程序在大多数情况下并不能完备穷举,总数会停在 2 31 − 1 2^{31}-1 231−1个构型位置上。Surge程序能够进行完备穷举,且总运行时间比MOLGEN小1~2个数量级。
此外,
Surge还有内存小等诸多优势,具体请看文献。下面介绍一下
Surge的工作流程。工作流程
Surge包含3个主要的工作步骤,分别对应nauty程序包中的geng.c, vcolg.c, multig.c。其中
geng.c是主流程,和原版本几乎一致。vcolg.c, multig.c体量较小,作者在surge.c中重写了一下,并通过surgeproc函数注入到了geng.c内部。函数调用关系如下图所示: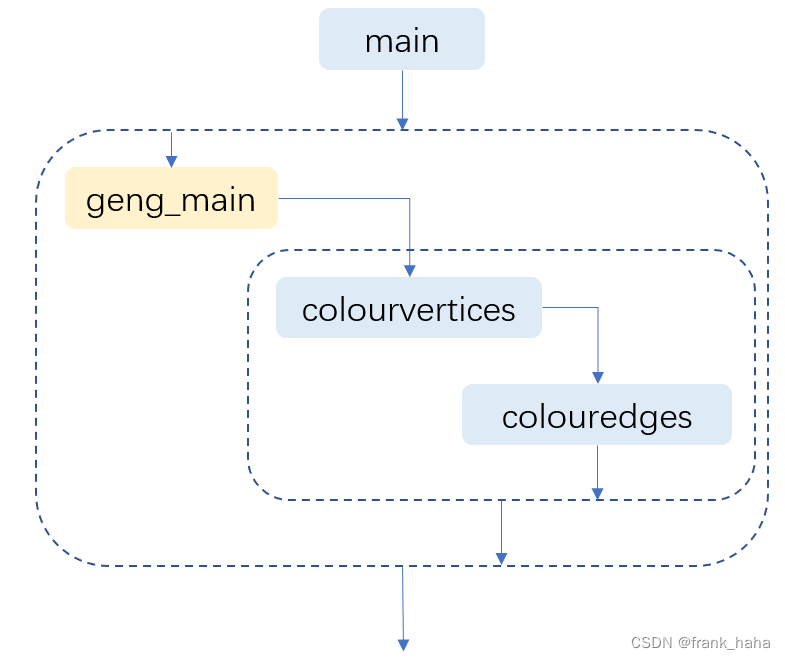
注:
geng_main设为黄色,表示其由外部独立文件组成。三个主要程序的功能如下图所示:
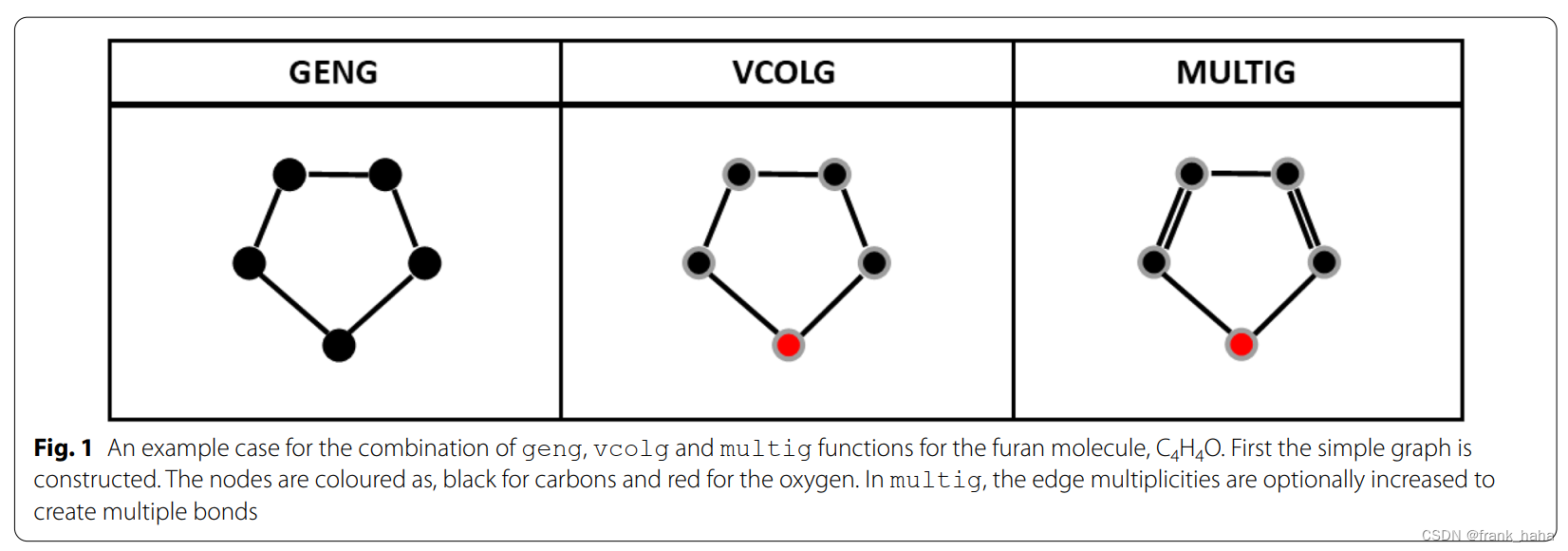
geng负责穷举所有的图。这种图不具备点和边的性质。vcolg负责对第一步产生的图点染色。所谓点染色,指把不同原子类型分配给各个顶点。multig负责对第二步产生的图进行边染色,即分配不同的边类型。
三个程序的主要思路相差不大,和 “
nauty求解图自同构群 ” 的思路一致,均为 DFS 算法。相关链接可以参考我之前一篇文章:判断图同构大杀器—nauty算法下面我以点染色算法为例简要介绍工作原理。
点染色算法
自同构群去冗余
点染色算法的前提是图和图的自同构群均已知。使用自同构群去冗余可以简化为如下场景:
一串二进制数,比如说
0100111。图的自同构群指,通过交换某两个字的位置,在图论的视角下,二者是等价的,只有一个是正则化、合法的。也就是说
1000111和0100111这两串数字所代表的特定图可能是一致的,如果一致,则在一定规则下,二者中仅有一个是正则的名称,而另一种是冗余的名称。我们只需要保存前者。化学套用场景
我们都知道,分子的真实结构是三维的。化学信息学处理类似数据会将其看成二维的分子图。而群论的描述对象更加抽象,将二维分子图转化为了一串数字,也就是每个原子对应的 Label 。此外,不同原子还有不同的颜色,也有对应的抽象表达。这里下篇文章会细讲,此处仅需要知道,群论的对象是一串一维的数字,经过了两次压缩,如下图所示:
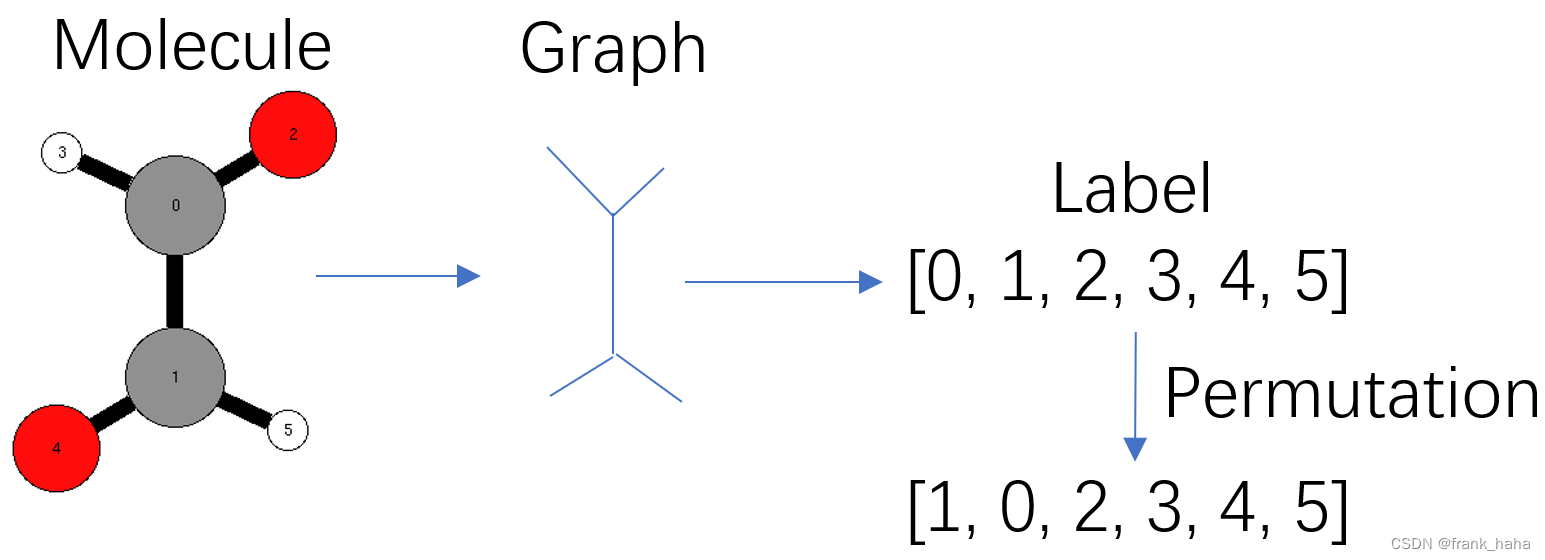
另一个比较重要的概念是,交换(Permutation, 直译是排序)。一种交换的场景如上图所示,序号为 0,1 的两个原子进行交换。从化学视角来看,这种交换不会改变分子结构,因此我们称交换前后的分子是同构的。
结合上一小节,我们知道,自同构群的作用就是不停对数组交换,相当于一个 if 模块,能够筛选出群论视角下不同构的数组。利用这样的性质我们可以解决如下问题:- 一个分子图有 7 个原子,我们设 C 对应 0, N 对应 1,
0100111则对应一种 C 3 N 4 \rm C_3N_4 C3N4 的异构体。 - 我们“穷举”出所有可能的数组,则每一个数组对应一个异构体。
- 在分子骨架确定的条件下,使用自同构群( if 模块)过滤出所有不同构的数组,对应所有异构体。
在
debug模式下,我认为,vcolg是这样运作的:首先是叶节点的遍历,在遍历过程中,如果一个状态通过了自同构检测,则从该状态开始进行亚叶节点的遍历。未通过自同构检测的组合,不会进行回溯,由此实现剪枝。所以说,这是一种 DFS 算法。
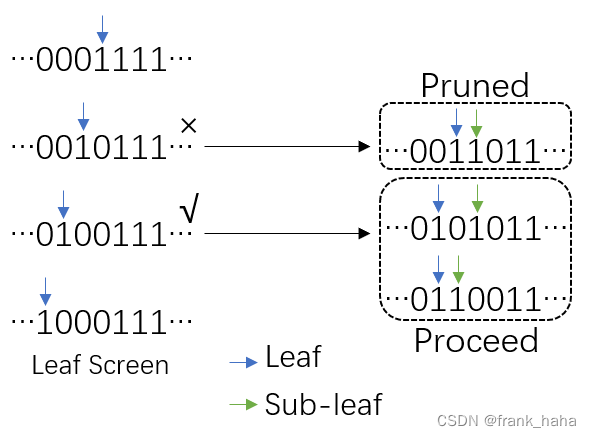
后续如果有更深的理解,会再写文分享。 -
相关阅读:
关于单片机CPU如何控制相关引脚
ChatGPT AIGC自动生成多条件复杂计算函数
uni-app点击复制指定内容(点击复制)
HIVE自定义UDTF函数
VirtualBox安装Centos
[软考中级]软件设计师-计算机网络
数据分析,从了解你的数据开始,数据探索性分析工具包pandas-profiling
C++ DAY06 c++多态
流媒体分析之rtmp ffmpeg 实现-两种技术实现
用DIV+CSS技术设计的公益主题网站——防止电信诈骗(web前端网页制作课作业)
- 原文地址:https://blog.csdn.net/frank_haha/article/details/128136886