L. Paid Leave(贪心)[CCPC Finals 2021]

题目如下：

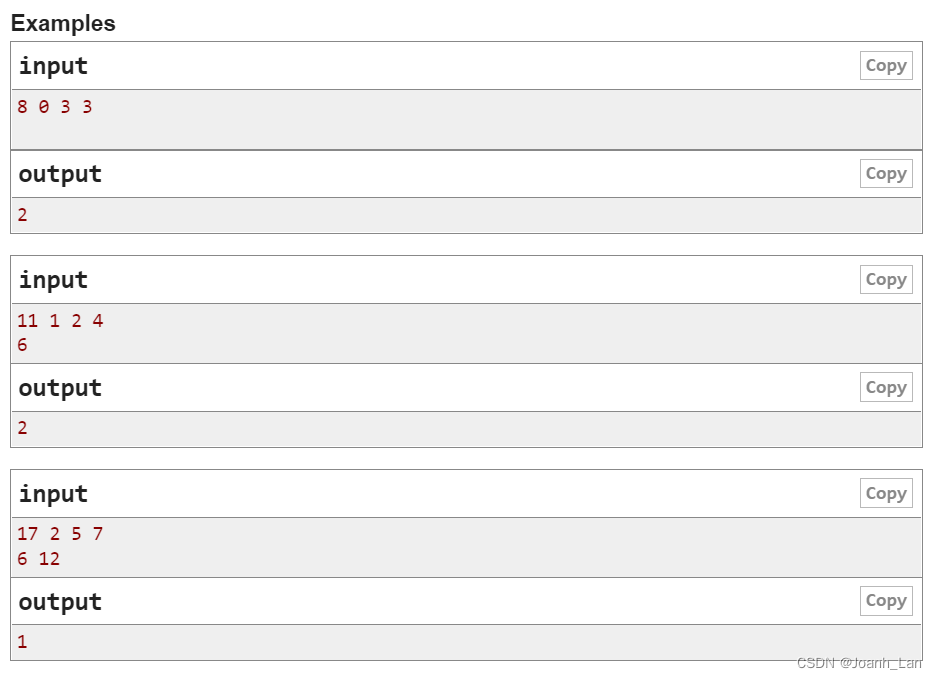
思路 or 题解

我们可以先只考虑第一段(两个休息日之间)

白色为休息日，蓝色为工作日
我们思考，如果在满足题意的条件下，如何安排额外的休息日可以使答案更优：
贪心可得：额外的休息日尽量往后安排一定不会使答案变差
所以我们把额外的工作日都安排到满足题意的最后面

第一段我们如何构造：
x[工作] 1(休息) y-x(工作) 1休息 x[工作] 1(休息) y-x(工作) 1休息 ... ...

我们可以发现循环节
循环节的长度为：$x+1+y-x+1=y+2$
进行推广至任意段我们如何操作才可以使答案最优？
约定:
last 代表上一次休息后连续工作的天数
ans 代表我需要添加的额外休息日的天数
ans += (r - l + 1) / (y + 2) * 2;
注：$\times 2$ 是因为一个完整的循环节有两个额外的休息日
剩余的长度：tt = (r - l + 1) % (y + 2);
如果 $tt>last$ 我们需要再添加一个额外的休息日

if (tt > last)
{
	tt -= last;
	ans++, tt --;
}
1
2
3
4
5

更新 $last$
last = min(x, y - tt);

我们将 第 $0$ 天， 第 $n+1$ 天认为是休息日，这样处理起来更加方便！（：

AC代码如下：

#define int long long
int n, m, x, y;
void solve()
{
    vector<int> v;
    cin >> n >> m >> x >> y;
    v.push_back(0);
    for (int i = 1; i <= m; i++)
    {
        int tt; cin >> tt;
        v.push_back(tt);
    }
    v.push_back(n + 1);
    int ans = 0;
    int last = x;
    for (int i = 1; i < v.size(); i++)
    {
        int l = v[i - 1] + 1, r = v[i] - 1;
        ans += (r - l + 1) / (y + 2) * 2;
        int tt = (r - l + 1) % (y + 2);
        if (tt > last)
        {
            tt -= last;
            ans++, tt --;
        }
        last = min(x, y - tt);
    }

    cout << ans << '\n';
}
signed main()
{
    buff;
    solve();
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35