第五站：操作符（终幕）（一些经典的题目）

目录

一、分析下面的代码

二、统计二进制中1的个数

解一：（求出每一个二进制位，来统计1的个数）

解二：（利用左我们移或右移操作符和按位与）

解三：（效率最高的解法，利用n=n&(n-1)求解）

举一反三：

三、打印整数二进制的奇数位和偶数位

解一：（暴力求解法）

解二：（利用位操作符）

 四、求两个数二进制中不同位的个数

解一：（利用移位操作符和按位与）

 解二：（异或操作符求解）

五、 获取月份天数

解一：（采用switch语句）

 解二：运用一个数组来存放天数

 六、一个经典的必错题！（算术转换）

七、序列中删除指定数字

解一：两层遍历，后面元素往前覆盖的解法

解二： 利用两个下标来求解

总结

---

一、分析下面的代码

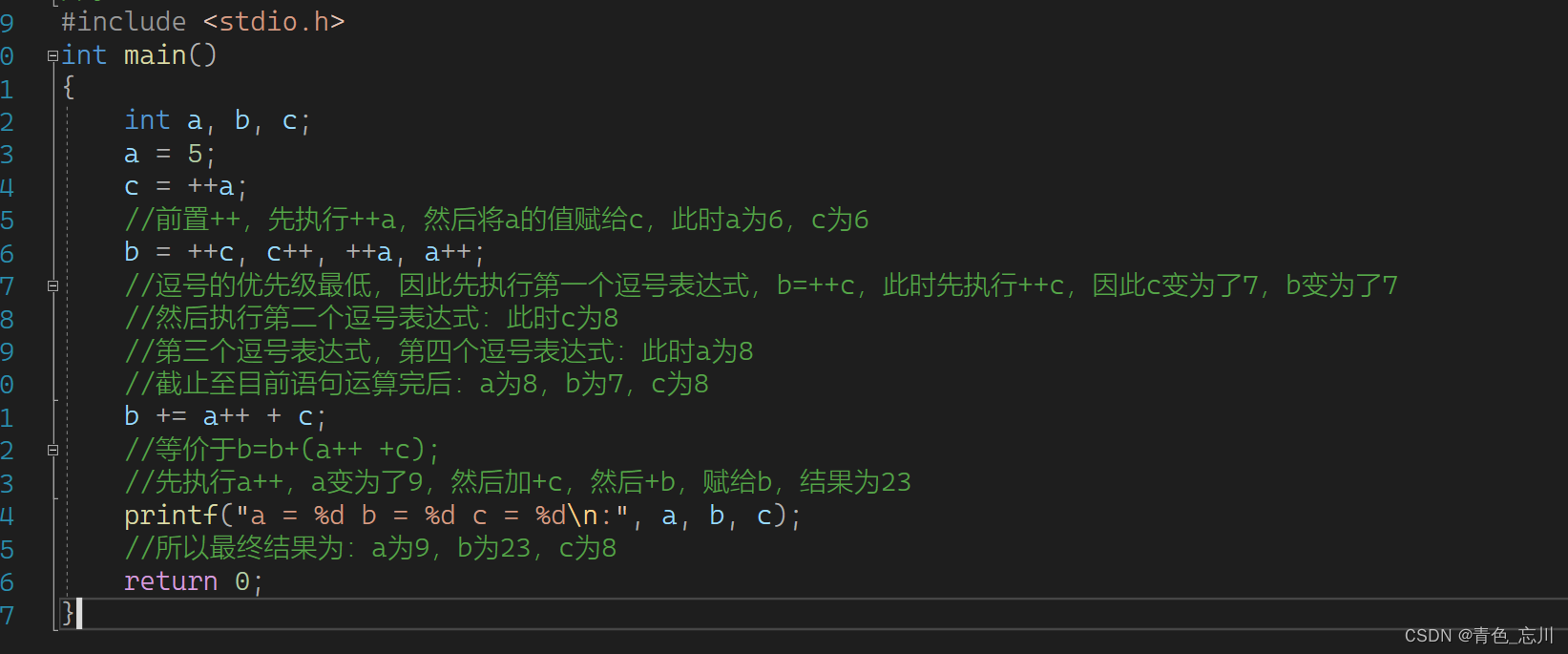
分析下面的代码，并给出运行结果。

#include <stdio.h>
int main()
{
	int a, b, c;
	a = 5;
	c = ++a;
	b = ++c, c++, ++a, a++;
	b += a++ + c;
	printf("a = %d b = %d c = %d\n:", a, b, c);
	return 0;
}

解析：这道题其实就是考察优先级的问题。在这里需要注意的是逗号的优先级最低，因此在第七行代码中，是先将c赋给了b，然后才继续往下的逗号运算的。这里很容易出现错误。

二、统计二进制中1的个数

题目描述：输入一个整数 n ，输出该数32位二进制表示中1的个数。其中负数用补码表示。

链接：二进制中1的个数__牛客网
来源：牛客网

解一：（求出每一个二进制位，来统计1的个数）

我们知道求一个数的二进制是采用取模，和除法的运算来实现的。所以我们可以利用这个思想来进行求解。定义一个计数器count，求出每一个二进制位，如果等于1，则count++

代码如下

#include<stdio.h>
int Numberof1(int n)
{
	int count = 0;
	while (n)
	{
		if (n % 2 == 1)
		{
			count++;
		}
		n = n / 2;
	}
	return count;
}
int main()
{
	int n = 0;
	scanf("%d", &n);
	int ret = Numberof1(n);
	printf("%d", ret);
	return 0;
}

我们测试后，发现对于正数，都是没有问题的，但是如果输入负数的话，就会出现问题。如下图所示

 

 因此我们需要进行优化代码，其实题目要求说，负数用补码来代替，但是他这里的运算是直接对原码翻译成的十进制数进行运算的。而数据在内存中存储的是补码，所以其实我们完全可以使用一个unsigned来进行修饰。这样就把我们的补码当作原码来进行运算了。

代码如下所示

#include<stdio.h>
int Numberof1(unsigned int n)
{
	int count = 0;
	while (n)
	{
		if (n % 2 == 1)
		{
			count++;
		}
		n = n / 2;
	}
	return count;
}
int main()
{
	int n = 0;
	scanf("%d", &n);
	int ret = Numberof1(n);
	printf("%d", ret);
	return 0;
}

运行结果如下图所示

 虽然这种解法经过我们测试后是没有问题的，但是这种解法在我们的牛客网平台其实是过不去的，因为我们这个已经改了函数的参数类型了，而题目要求是不能修改，所以我们还需要另寻他法。

解二：（利用左我们移或右移操作符和按位与）

其实我们要注意到，这道题目是针对二进制的，二进制在计算机内部是补码的形式。我们的第一种方式还需要将补码弄成原码，才成功做出来题。这种方法虽然可以，但是我们其实没有必要这么麻烦。我们可以直接对补码进行操作。而对补码进行操作的操作符就是我们的位操作符了，位操作符一共有&，|，^，>>，<<这五种

我们观察这五种操作符，我们可以想到，按位与&有一个比较良好的性质，任何一个二进制位按位与1结果仍然为该二进制位。因此我们可以思考让这个数的每一位都按位与1。如果结果为1，则count++。那么如果让每一位都能按位与1呢？其实我们可以使用移位操作符，这里我们既可以左移1，也可以右移该二进制序列。两种方法皆可

代码如下

#include<stdio.h>
int Numberof1(int n)
{
	int count = 0;
	int i = 0;
	for (i = 0; i < 32; i++)
	{
		if (((n >> i) & 1 )== 1)
		{
			count++;
		}
	}
	return count;
}
int main()
{
	int n = 0;
	scanf("%d", &n);
	int ret = Numberof1(n);
	printf("%d", ret);
	return 0;
}

 而我们将这个代码的函数部分放到牛客网上运行，可以显示运行通过

 当然除此以外，其实还可以采用按位或的性质，任何一个二进制位按位或0，结果仍然为该二进制数。这种方法与上述方法完全是对偶的，因此不在赘述。

解三：（效率最高的解法，利用n=n&(n-1)求解）

解二中，方法虽然可以实现，但是效率太低，因为无论是多大的数，都需要执行32次循环才可以解决问题。因此我们考虑使用这个公式，为什么是要利用这个公式呢？我们举一个例子，模拟一下这个公式的执行

 我们发现，其实每执行一次，相当于n少了一个1.因此我们可以每执行一次，count++就会实现我们的目标。其实从我们数学的角度来思考，n每减1，然后按位与n所得到的结果就会使得我们原来的n少一个1

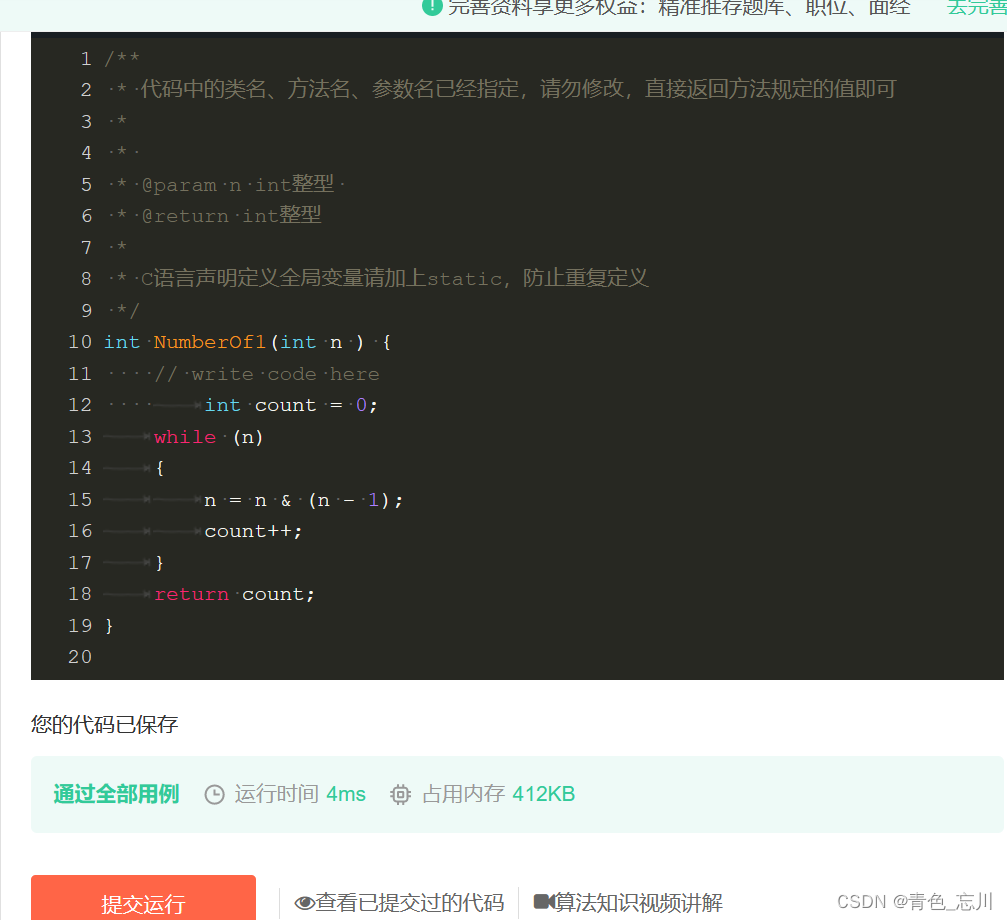
代码如下所示

#include<stdio.h>
int Numberof1(int n)
{
	int count = 0;
	while (n)
	{
		n = n & (n - 1);
		count++;
	}
	return count;
}
int main()
{
	int n = 0;
	scanf("%d", &n);
	int ret = Numberof1(n);
	printf("%d", ret);
	return 0;
}

牛客网上运行结果为

举一反三：

关于这道题，我们其实还可以引发一些思考，我们看一下这道题

写出一个代码，判断某一个数是否是2的次方

这个题目当然可以用暴力破解。但是我们其实有效率更高的方式，因为某一个数是2的次方，那就说明，该数的二进制序列中只有一个1。由此题目豁然开朗、迎刃而解。我们上面的三种方式可以完成这个判断

利用解三完成的代码如下

#include<stdio.h>
int main()
{
	int n = 0;
	scanf("%d", &n);
	int flag = 0;
	if ((n & (n - 1)) == 0)
	{
		flag = 1;
	}
	if (flag == 1)
	{
		printf("是2的次方");
	}
	else
	{
		printf("不是2的次方");
	}
	return 0;
}

三、打印整数二进制的奇数位和偶数位

题目描述：输入一个数，打印出他二进制的奇数位和偶数位

解一：（暴力求解法）

对于二进制的题目，思考最少，最简单，最暴力的方法就是求出每一位，然后进行打印出奇数位和偶数位，值得注意的是，数据在内存中存储的是二进制位，因此会出现负数的问题，因此我们需要使用unsigned进行修饰。来避免一些问题

代码如下

#include<stdio.h>
int main()
{
	unsigned n = -1;
	int i = 0;
	unsigned int tmp = 0;
	//获取奇数位
	tmp = n;
	for (i = 1; i <= 32; i = i + 2)
	{
		printf("从右往左第%d位： %u\n",i, tmp % 2);
		tmp = tmp / 2;
		tmp = tmp / 2;
	}
	//获取偶数位
	tmp = n;
	for (i = 2; i <= 32; i = i + 2)
	{
		tmp = tmp / 2;
		printf("从右往左第%d位： %u\n", i, tmp % 2);
		tmp = tmp / 2;
	}
	return 0;
}

解二：（利用位操作符）

第一种方法实在太暴力，效率也很低。既然是跟二进制相关，那肯定要考虑位操作符相关的方法。有了前面第二题的第二中方法的参考，我们也可以按照移位操作符和按位与来实现一下

代码如下：

#include<stdio.h>
void Print(int n)
{
	int i = 0;
	//打印奇数
	printf("打印奇数：");
	for (i = 30; i >= 0; i = i - 2)
	{
		printf("%d ", (n >> i) & 1);
	}
	printf("\n");
	//打印偶数
	printf("打印偶数：");
	for (i = 31; i >= 0; i = i - 2)
	{
		printf("%d ", (n >> i) & 1);
	}
	printf("\n");
}
int main()
{
	int n = 0;
	scanf("%d", &n);
	Print(n);
}

运行结果为

 四、求两个数二进制中不同位的个数

链接：两个整数二进制位不同个数__牛客网
来源：牛客网

输入两个整数，求两个整数二进制格式有多少个位不同

解一：（利用移位操作符和按位与）

这种思想我们在第二题，第三题均已经提到过。我们继续来利用这种思想来完成这道题

代码如下：

#include<stdio.h>
int main()
{
	int n = 0, m = 0;
	int count = 0;
	scanf("%d %d", &m, &n);
	int i = 0;
	for (i = 0; i <= 32; i++)
	{
		if (((n >> i) & 1) != ((m >> i) & 1))
		{
			count++;
		}
	}
	printf("%d", count);
	return 0;
}

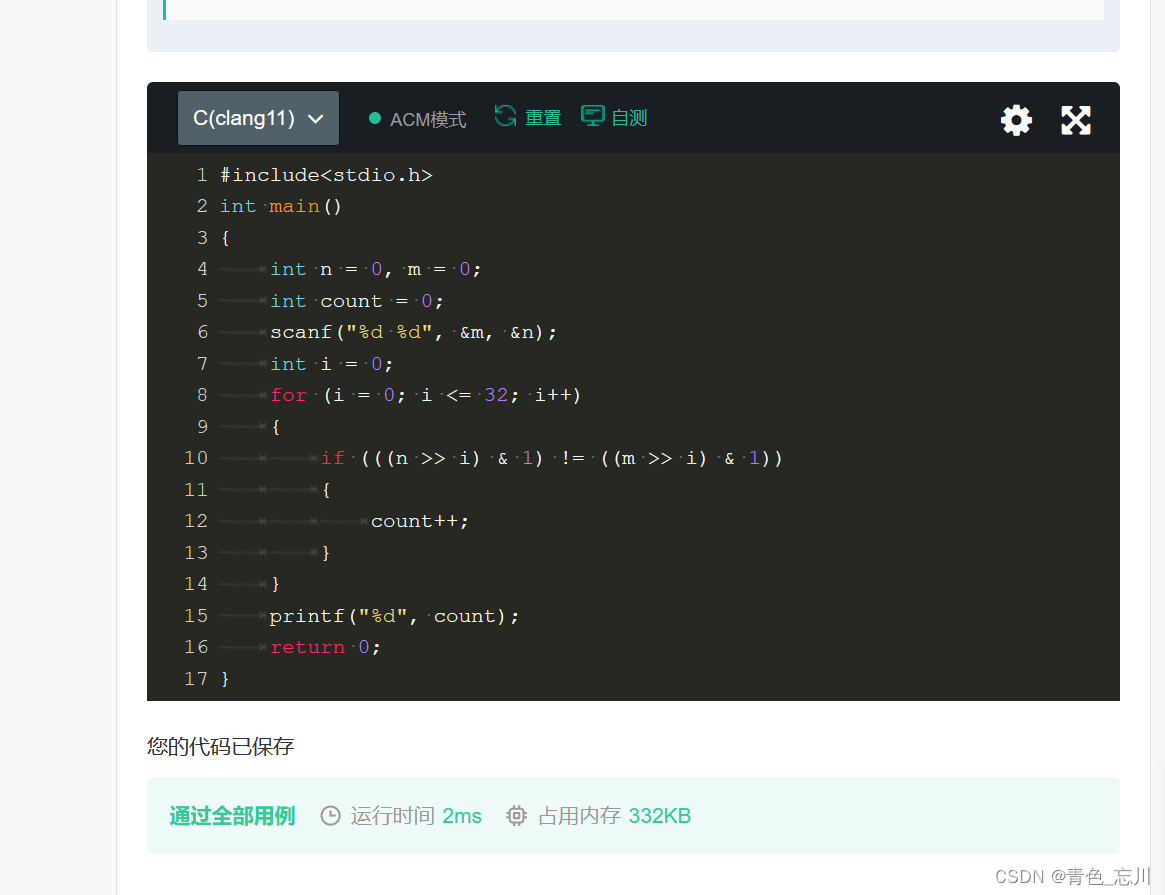
 解二：（异或操作符求解）

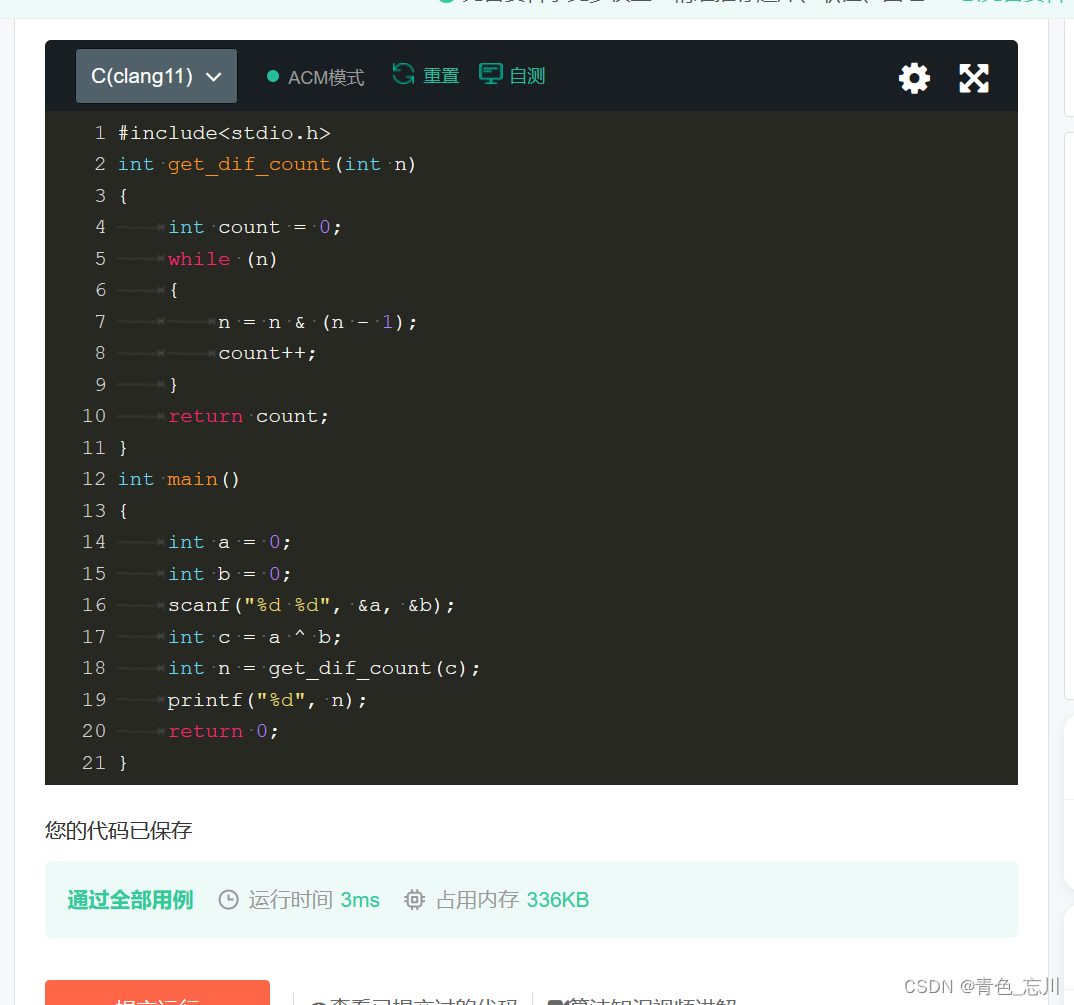
上面的运行后效率是比较低的，那么有没有比较高的效率呢？我们说是有的，我们将两个数异或，能得到一共全新的二进制序列，对于这个二进制序列，我们就只需要统计这个二进制序列中1的个数，即可得到答案，而统计二进制序列中1的个数，这正好就是第二个题

代码如下：

#include<stdio.h>
int get_dif_count(int n)
{
	int count = 0;
	while (n)
	{
		n = n & (n - 1);
		count++;
	}
	return count;
}
int main()
{
	int a = 0;
	int b = 0;
	scanf("%d %d", &a, &b);
	int c = a ^ b;
	int n = get_dif_count(c);
	printf("%d", n);
	return 0;
}

五、 获取月份天数

    获取月份天数链接：获取月份天数_牛客网

   来源：牛客网

解一：（采用switch语句）

对于这种，题目我们可以直接采取switch语句，唯一需要注意的是2月需要判断闰年

代码如下：

#include<stdio.h>
int is_leap_year(int y)
{
	if ((y % 4 == 0) && (y % 100 != 0) || (y % 400) == 0)
	{
		return 1;
	}
	return 0;
}
int get_day_of_month(int y, int m)
{
	int day = 0;
	switch (m)
	{
	case 1:
	case 3:
	case 5:
	case 7:
	case 8:
	case 10:
	case 12:
		day = 31;
		break;
	case 4:
	case 6:
	case 9:
	case 11:
		day = 30;
		break;
	case 2:
		day = 28;
		if (is_leap_year(y) == 1)
		{
			day++;
		}
	}
	return day;
}
int main()
{
	int y = 0, m = 0;
 
	while (scanf("%d %d", &y, &m) == 2)
	{
		int ret = get_day_of_month(y, m);
		printf("%d\n", ret);
	}
 
	return 0;
}

 解二：运用一个数组来存放天数

上面switch语句写法固然可以，但显得太过于啰嗦，我们使用一个数组，可以使代码更简洁

#include <stdio.h>
int is_leap_year(int y)
{
	if ((y % 4 == 0) && (y % 100 != 0) || (y % 400) == 0)
	{
		return 1;
	}
	return 0;
}
int main() {
	int y, m;
	while (scanf("%d %d", &y, &m) == 2)
	{
		int day[] = { 31,28,31,30,31,30,31,31,30,31,30,31 };
		if (is_leap_year(y) == 1)
		{
			day[1]++;
		}
		printf("%d\n", day[m - 1]);
	}
	return 0;
}

 六、一个经典的必错题！（算术转换）

如下所示，阅读代码，并给出答案。

#include 
int i;
int main()
{
    i--;
    if (i > sizeof(i))
    {
        printf(">\n");
    }
    else
    {
        printf("<\n");
    }
    return 0;
}

很多人一看这道题，觉得太简单了，直接就是-1<4,选<，这样做就进入了陷阱了。

我们先看一下运行结果，为>

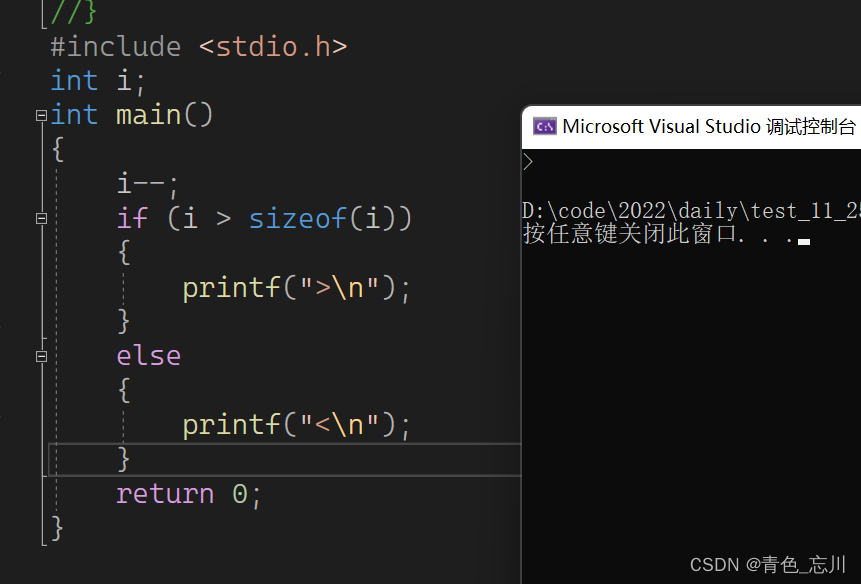
 那么这是为什么呢？其实这是因为中间发生了算术转换。i是一个全局变量，默认是0，然后i--，此时i变为了-1。但是sizeof计算的结果类型是size_t，而是size_t就是unsigned int。-1是一个普通整型，按照我们之前所说的要根据层级，向上发生算术转换，因此-1变为了unsigned int类型，而-1的补码是11111111 11111111 11111111 11111111，他变为unsigned int类型后，原码就是补码了，导致原码很大。因此-1就被隐式转换成了一个超级大的数，他当然大于4了。因此结果就是>

七、序列中删除指定数字

链接：序列中删除指定数字_牛客网

来源：牛客网

解一：两层遍历，后面元素往前覆盖的解法

这个方法算是一个暴力的解法。我们直接去遍历这个数组，遇到删除的元素，将后面的整体往前挪一个单位，但是这样的话要注意某一个位置出现连续重复数字，为了避免这种情况，我们挪之后，还需要重新检验一下当前的i是否需要删除

代码如下：

#include <stdio.h>
 
int main() {
    int n=0;
    scanf("%d",&n);
    int arr[n];
    int i=0;
    for(i=0;i<n;i++)
    {
        scanf("%d",&arr[i]);
    }
    int num=0;
    int tmp=n;
    scanf("%d",&num);
    for(i=0;i<tmp;i++)
    {
        if(arr[i]==num)
        {
            int j=0;
            tmp=tmp-1;
            for(j=i;j<tmp;j++)
            {
                arr[j]=arr[j+1];
            }
            i--;
        }
    }
    for(i=0;i<tmp;i++)
    {
        printf("%d ",arr[i]);
    }
    return 0;
}

解二： 利用两个下标来求解

我们可以这样想，我们先遍历我们的数组，然后定义两个变量i，j作为下标，我们可以通过这两个下标，当数组元素与待删除数字不相同时候，我们将i下标的数组元素赋给j下标的数组元素。然后j++，i++。当数组元素与待删除数字相同时，我们直接跳过该元素，只让i++，j不变。最后我们遍历数组的时候，j也刚好是我们数组的需要的大小。

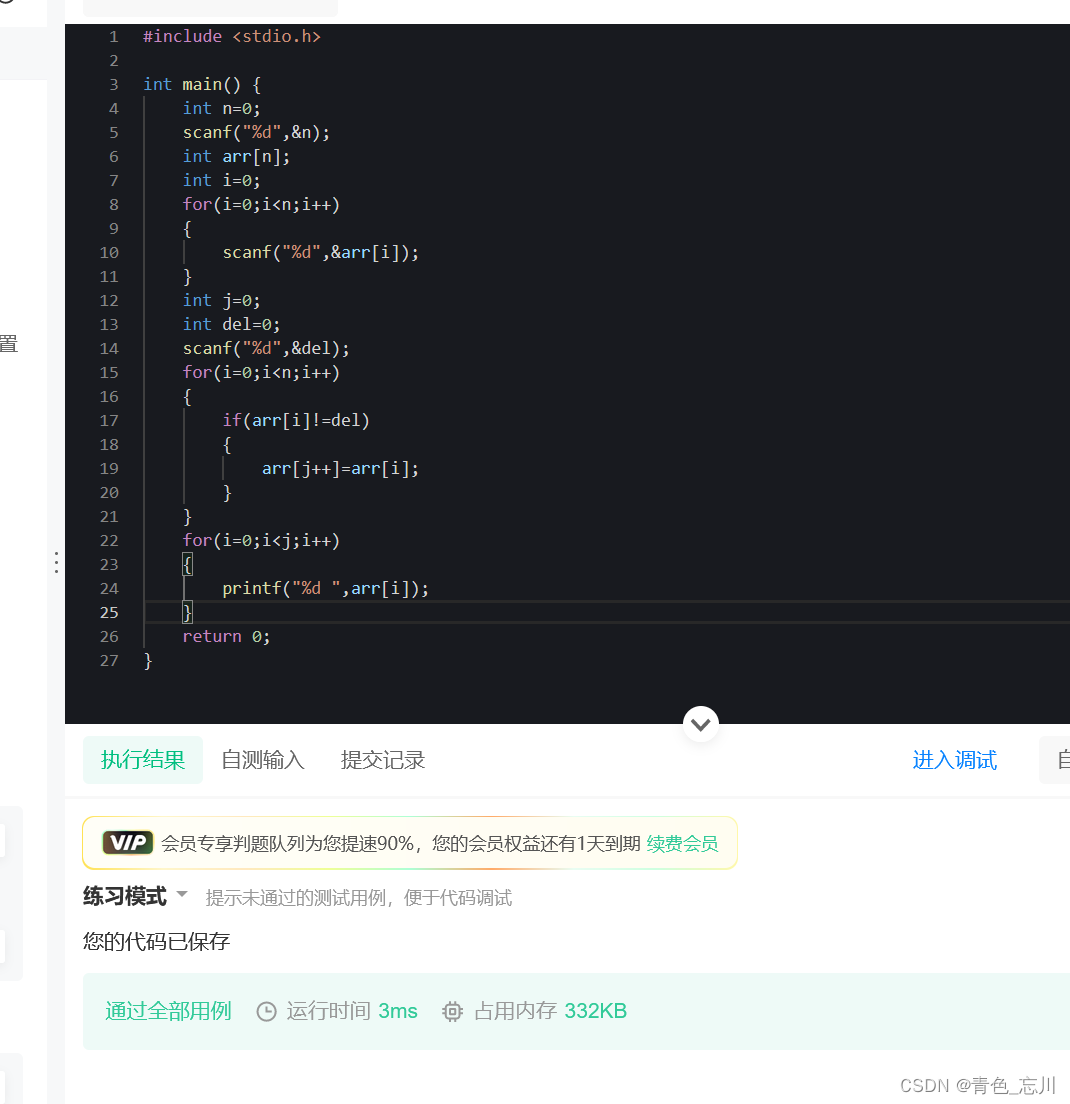
代码如下：

#include <stdio.h>
 
int main() {
    int n=0;
    scanf("%d",&n);
    int arr[n];
    int i=0;
    for(i=0;i<n;i++)
    {
        scanf("%d",&arr[i]);
    }
    int j=0;
    int del=0;
    scanf("%d",&del);
    for(i=0;i<n;i++)
    {
        if(arr[i]!=del)
        {
            arr[j++]=arr[i];
        }
    }
    for(i=0;i<j;i++)
    {
        printf("%d ",arr[i]);
    }
    return 0;
}

运行结果为

---

总结

本小节主要讲解了一些经典的题目，内容比较丰富，希望对大家有所帮助。不要忘记点赞+收藏哦！！！