数据库索引

目录

🐇今日良言:志在山顶的人，不会贪念山腰的风景。

🐉数据库索引

🐳1.概念

🐳2.使用 

🐳3.在mysql中的数据结构

---

🐇今日良言:志在山顶的人，不会贪念山腰的风景。

🐉数据库索引

🐳1.概念

难道说索引没有副作用吗?

其实不然:

1).索引会提高增删改的的开销.

    以一本书为例,有了目录确实会增加读者查找某个章节的速度,但是,当一本书已经定制好了,      此时,如果作者想要再新增内容,就需要连同目录一起新增,若要修改内容,目录也要修改,删除

    章节内容的话,目录也是要删除的.显而易见,目录会提高增删改的开销,索引也是同理.

2).索引会提高空间的开销

    构造索引需要额外的磁盘空间来保存.

    当一本书的内容足够多(数据库的数据库足够多),此时目录也是需要不少页的(索引也需要

    更多额外的磁盘空间)

🐳2.使用

1).使用场景

a.数据量较大，且经常对这些列进行条件查询。

b.该数据库表的插入操作，及对这些列的修改操作频率较低。

c.磁盘空间充足

2).SQL语句

 a.查看索引

基本语法: show index from 表名;

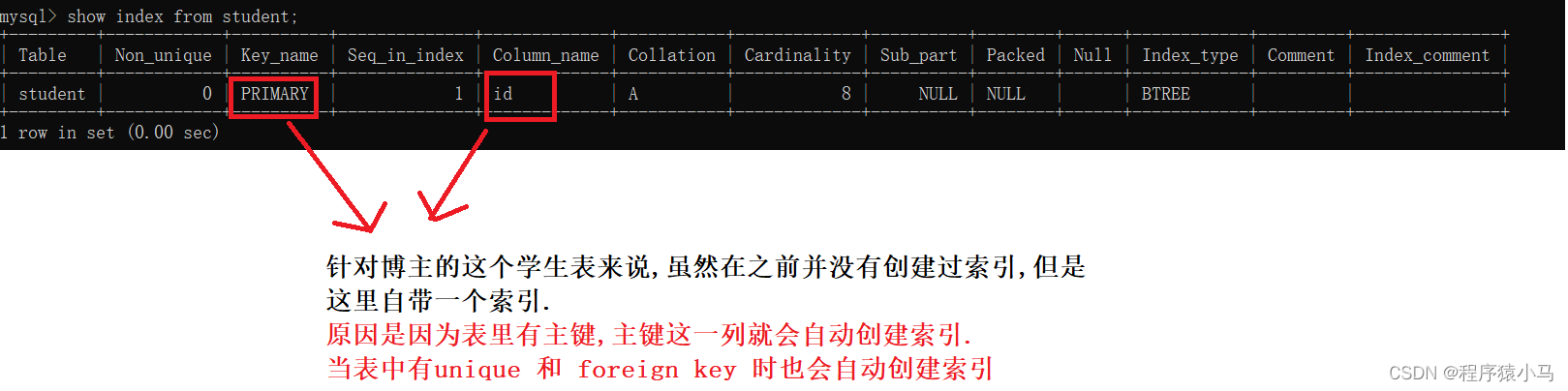
b.创建索引

基本语法:create index 索引名 on 表名(列名);

例:给上面学生表的name列创建一个索引

此时再去观察查看当前学生表的索引

 此时可以看出,name这一列有一个索引,这个就是针对名字这一列新加的索引.

 注意:

创建索引,最好是在表创建之初就创建好,否则,如果针对一个有很多很多记录的表来创建索引,是一个危险操作.

为什么说是一个危险操作?

这是因为,当为有很多记录的表创建索引时,会'吃掉'大量的磁盘IO,创建索引这个操作可能会花很长时间(几十分钟到几个小时,视数据量而定),而在这段时间内,数据库是无法正常使用的.

当创建好索引后,不需要手动使用,直接查询的时候就会自动进行索引操作,具体的这一次查询,实际上是否是在走索引,其实是不好预期的,可以使用explain这个关键字,显示出查询过程中,具体的使用索引的情况. 

c.删除索引

基本语法:drop index 索引名 on 表名;

例:删除刚刚为学生表姓名列创建的索引

 注意:删除索引操作,也是危险操作,也可能'吃掉'大量的磁盘IO

🐳3.在mysql中的数据结构

前面已经说过,索引主要就是为了加快查找速度,提起查找速度,不得不提以下这几个数据结构:

1).哈希表

这是数据结构中最重要的知识点,博主在之前的文章中有具体实现:

(2条消息) 哈希表（限定版）_程序猿小马的博客-CSDN博客

哈希表查找元素的时间复杂度是:O(1) 

 既然哈希表的查找速度如此之快,能不能做数据库的索引呢?

很遗憾,不适合,这是因为:哈希表只能比较相等,而无法进行范围查询,而我们的数据库查询经常是范围查询.

2).二叉搜索树

博主之前的代码实现:

(2条消息) 二叉搜索树_程序猿小马的博客-CSDN博客

二叉搜索树查找元素的时间复杂度是O(logN)

二叉搜索树由于树里的元素是有序的,当我们要查一定范围内的数据时,可以查询起点和终点,这样就可以得到这个范围内的数据.

但是,很遗憾,索引也没有使用二叉搜索树,这是因为:二叉意味着当元素个数多了的时候,树的高度就会比较高,树的高度就决定了查询时候元素的比较次数,而数据库进行比较都是要读硬盘的,此时效率就会很低.

3).N叉搜索树

N叉搜索树就是每个节点上有多个值,同时又有多个分叉,这种结构相对于二叉搜索树而言,树的高度就降低了.

其中的一种典型实现叫做B树

B树结构如下

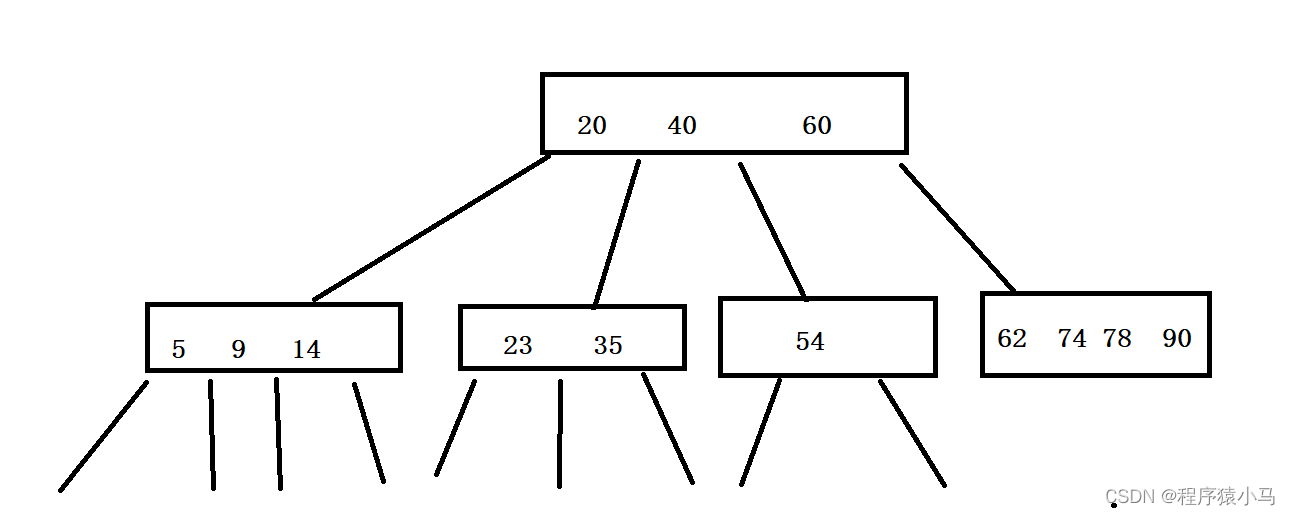
比较次数虽然没怎么减少(一个节点可能需要比较多次了),但是读写硬盘的次数减少了(每个节点都是在硬盘上的)

B树已经可以比二叉搜索树更适合做数据库的索引了,但是还不够,引入B+树,是对B树进行了进一步的改进

B+树

B+树就是为了索引这个场景量身定做的数据结构.

B+树结构如下:

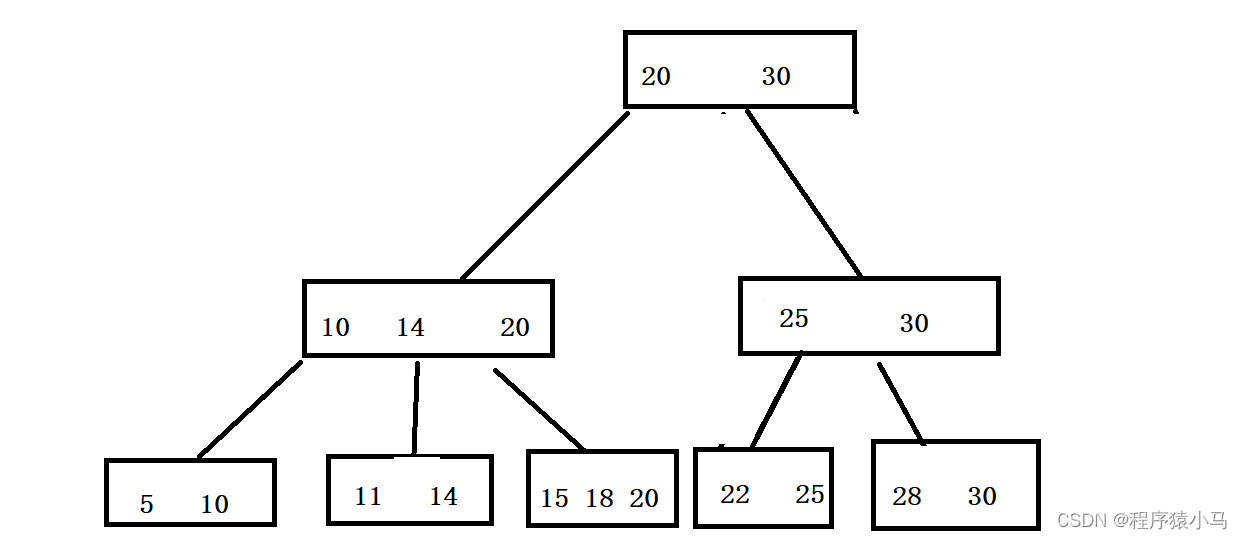
B+树的特点:

 1.B+树也是一个N叉搜索树,每个节点上可能包含N个key,N个key划分出N个区间.最后一个

    key就相当于最大值了.

2.父元素的key值会在子元素中重复出现,并且是以最大值的姿态出现的,

   这样的重复出现,导致了叶子节点就包含了所有数据的全集(非叶子节点中的所有值都会在

   叶子节点中体现出来)

3.会把叶子节点用类似链表的方式首尾相连,如下图:

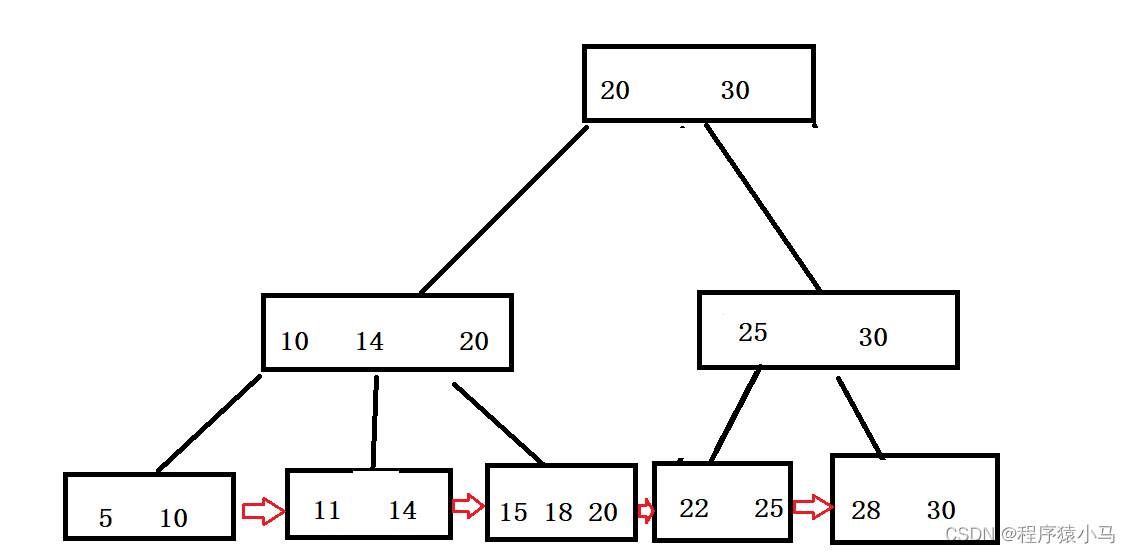
上述B+树的特点就带来了一些好处

1.作为一个N叉搜索树,高度降低下来,比较的时候,磁盘IO次数就比较少了(同B树)

2.更适合进行范围查询

3.所有的查询,都是要落在叶子节点上的,无论查询哪个元素,中间比较的次数差不多.

   查询操作比较均衡

   对于B树来说,可能是有的值查的快,有的查的慢,可能就不均衡了(在根节点或者深度不深

   的位置,都查的快)

   但是对于B+树,速度都是一样的(全部数据都在叶子节点)

4.由于所有的值都会在叶子节点中体现,因此非叶子节点,不必存表的真实记录(不必存数据行)

   只需要把所有的数据放到叶子节点上即可,非叶子节点只需要存索引列的值(比如存个id)

   所以说,数据库中看到的表可能是如下树形结构:

  

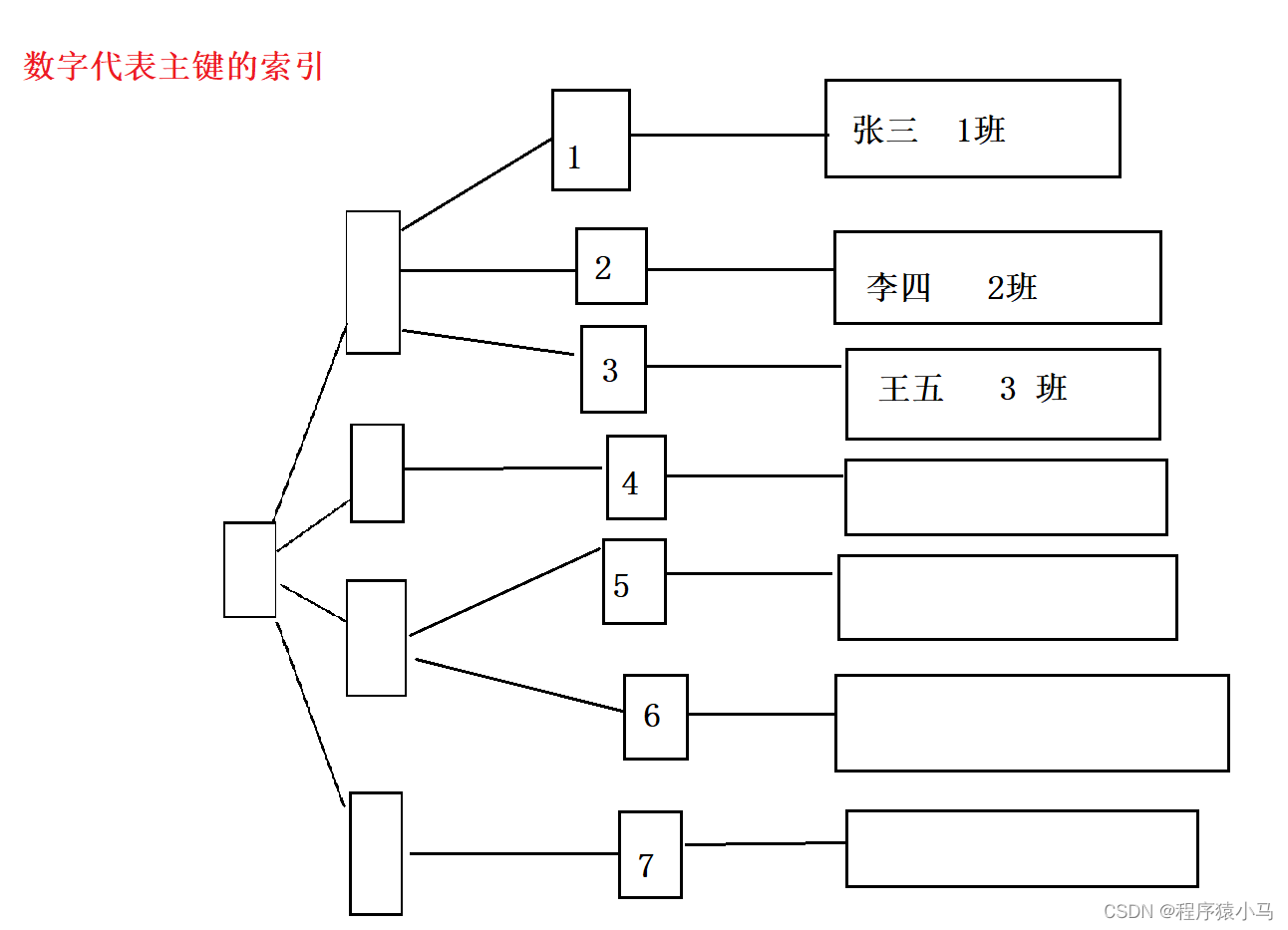
由于非叶子节点只存了简单id,没有存一整行,这就意味着非叶子节点占用的空间大大降低,有可能在内存中可以放进去缓存,更进一步的降低了硬盘IO,提高查询速度,本质上就是在减少硬盘IO次数.

对于带有主键的表,就是按照主键索引的B+树来组织的

有的表,不只是主键索引,还有别的非主键列,也有索引,针对这种情况,会构造另一个B+树,B+树非叶子节点里面都是存这一列里面的key(比如一堆学生姓名),到了叶子节点这一层,不是存之前的完整的数据行,而是存id,此时,如果使用主键列来查询,只要查一次B+树就可,如果是使用非主键列的索引来查询,则需要先遍历一遍索引列的B+树,再查一遍主键列的B+树,这个操作称为'回表'.

当然,也有可能是如下表组织结构