-
从模型容量的视角看监督学习
- 这几天看离线强化学习瞎想的,不一定正确,仅记录个人想法
1. 监督学习的本质
- 我认为监督学习的本质在于在过拟合和欠拟合之间取得平衡,捋一下逻辑
- 我们知道,如果模型复杂度相对数据复杂度过高,就会过拟合;反之模型复杂度相对数据复杂度过低,则会欠拟合
如果不知道,可以参考:李宏毅老师的课程
- 模型复杂度”、“模型容量”、“模型能表示映射关系的复杂程度”、“模型的假设空间大小” 这几个概念都是正相关的,下面讨论时会不严格地混用这些词
- 做好监督学习 = 最大限度地从数据中提取信息 = 在过拟合和欠拟合之间取得平衡 = 选择复杂度和数据复杂度差不多的模型 = 选择容量合适的模型
- 我们知道,如果模型复杂度相对数据复杂度过高,就会过拟合;反之模型复杂度相对数据复杂度过低,则会欠拟合
2. 容量视角下的模型选择、正则化和归纳偏置
-
记住我们的重点是控制模型容量,使之复杂度和给定的样本复杂度相匹配
-
在参数数量一致的情况下,全连接网络(或者说多层感知机)的容量是最大的
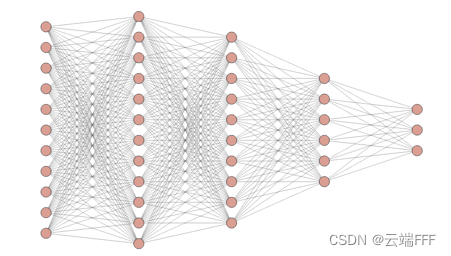
全连接网络不受任何限制,它能表示的映射关系是最多的,假设空间是最大的,这也导致其很容易过拟合,极大的假设空间大概率能涵盖一个完美拟合给定数据自身特征的模型,如果样本量不够大,数据自身特征的普遍性和代表性差,习得模型的泛化性会很差 -
从这个角度考虑,常见的正则化方法都是在隐式地限制模型容量,例如
L2正则化,通过调整损失函数控制优化方向,间接地限制最后学到模型的参数范围dropout正则化,通过随机失活神经元,防止模型输出被某些神经元主导,间接地限制最后学到模型的参数范围
上面这两种常见的正则化都是限制参数中出现极端值,也就是隐式地从假设空间中挖掉了被极端值主导的部分,一般而言无论什么问题我们都不想要这种极端的模型,因此这些正则化方法几乎哪里都能见到
-
在各种论文中我们常常见到作者修改损失函数,往里加一些正则化项之类的,如果从容量角度考虑,就是作者注意到了问题或者数据的某些潜在关系,然后增加正则化项控制优化方向,隐式地调节模型容量,使模型复杂度和样本复杂度更加匹配,从而能在使用相同样本的情况下得到更好的效果
-
进一步地,控制模型容量更直接的方法就是直接修改模型结构,从而硬性地,显式地限制模型假设空间的大小。当然,这个限制是有方向的,我们想要针对性地保留假设空间中能更好地表示给定数据特征的部分,这就需要针对问题去设计模型了结构了,例如
- 针对图像的平移不变性,在 CV 领域出现了 CNN,将全连接层替换为卷积层,通过固定的卷积核扫过图像来提取特征
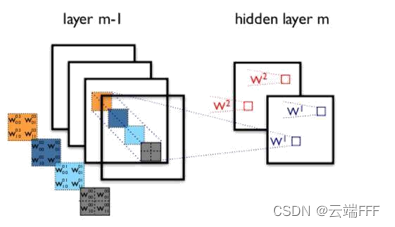
- 针对序列数据的长距离相关性,在 NLP 领域出现了 Transformer,将全连接层替换为 self-attention 层,通过 QKV 矩阵直接长跨度梯度提取特征
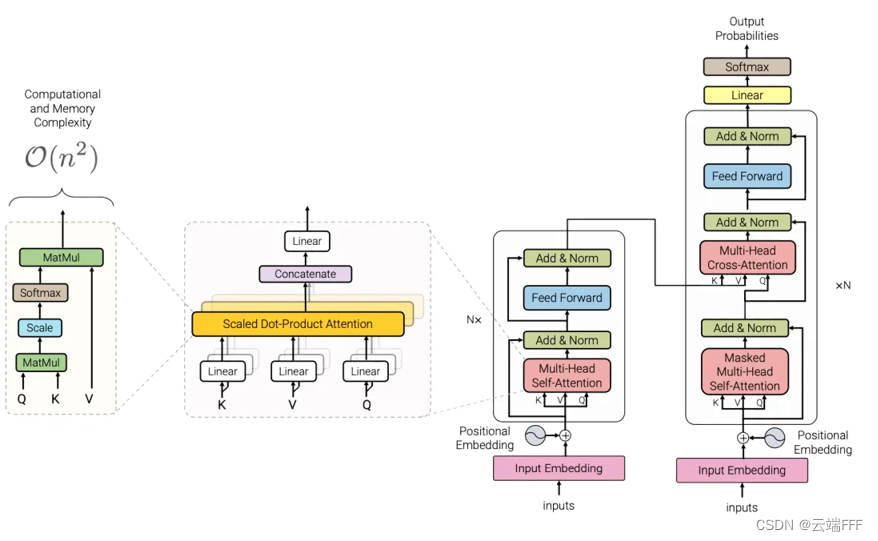
- 进一步的还出现了神经网络结构搜索(NAS)领域,专门致力于寻找最好的网络结构,这也能从容量的角度进行解释。极端情况下,我们甚至可以使模型的容量足够小(假设空间足够小,归纳偏置足够强),以致于可以直接使用随机参数执行任务而无需任何训练,这可以参考 论文翻译 —— Weight Agnostic Neural Networks 权重无关神经网络
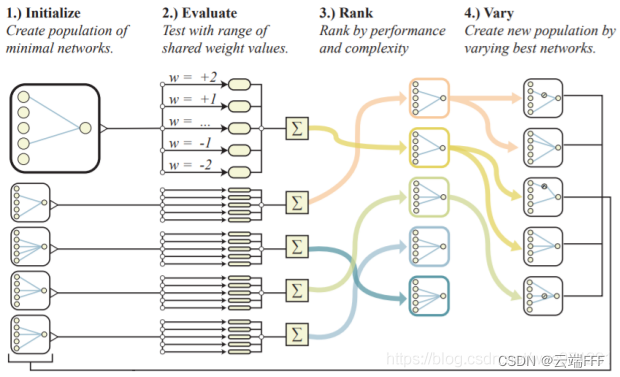
总之,不同的网络结构,都可以理解为将全连接网络中的一些层替换为特殊设计的层,也就是从全连接网络对应的最大的假设空间中根据数据特性保留一部分,保留的不同部分,决定了模型不同的
归纳偏置 - 针对图像的平移不变性,在 CV 领域出现了 CNN,将全连接层替换为卷积层,通过固定的卷积核扫过图像来提取特征
3. 几点启发
-
针对同一个任务,归纳偏置更强的模型复杂度更低,相同样本复杂度(可简单理解为相同样本数量)下更不容易过拟合;归纳偏置更弱的模型能表示的假设空间更大,能刻画的映射关系更复杂,如果有足够样本的话其性能上限更高。这可以解释为何 transformer 在各个领域乱杀,一方面因为各种监督学习问题大都能转换为序列预测问题,另一方面 transformer 中的 self-attention 的约束足够弱,其表示能力足够强,如下所示,纯 self-attention 层和全连接层组成的 BERT 结构几乎和全连接的 MLP 差不多了
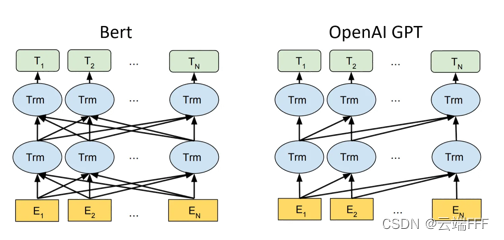
这一点已经在 CV 领域得到验证,直接用 BERT 模型做图像分类的 VIT 方法,和使用 CNN resnet 结构做图像分类的 BIT 方法相比,预训练+微调后的性能如下
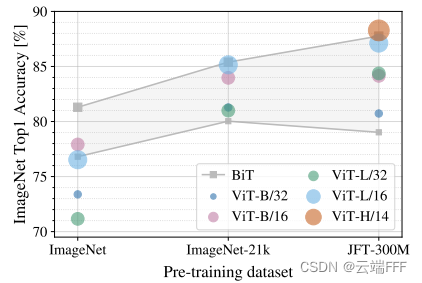
可见随着预训练数据集的增大,VIT 从不及 BIT 不断提升到超过 BIT -
如果两个任务 A B 足够相似,那么它们所需模型的归纳偏置应当也很相似,A 任务中表现良好的模型,很可能只要进行正则化等简单的修改就能直接在 B 任务表现良好。在 Offline RL 领域,就有直接把 Online RL 方法 TD3 的 actor 加上简单 BC 正则项而得到的 TD3 + BC 方法,表现很不错
-
如果仔细设计网络宽度和深度,使模型复杂度合适,那么简单的 MLP 也能在各种问题中到达和复杂网络结构一样的效果。这个结论应该在多个领域中被验证过,Offline RL 领域的例子可以举最近的 RvS 论文
-
相关阅读:
论文:Cover letter,添加基金项目:山东省自然科学基金
[4G/5G/6G专题基础-160]: 5G双链接与MCG/SCG/PCell/PSCell/SCell
HyperBDR云容灾深度解析五:全程助力业务级容灾,实现分钟级RTO业务恢复
【好文推荐】openGauss 5.0.0 数据库安全——全密态探究
第三篇,芯片启动和时钟系统
《福格行为模型》笔记 --- ta为什么总是想得多做得少
Lecture 3 Process Concept(进程概念)
[MATLAB]进阶绘图
什么台灯最好学生晚上用?开学适合学生用的护眼台灯推荐
腾讯云服务器使用教程,手把手教你入门
- 原文地址:https://blog.csdn.net/wxc971231/article/details/128107548