-
无线传感器网络:定位、安全与同步
Localization
为什么在 WSN 中需要进行定位?
- 收集到的关于物理现象的信息需要与传感器节点的位置相关联,来提供更有价值的信息
- WSN 可在监测应用中用于追踪某些物体,这就需要将传感器节点的位置信息纳入追踪算法
- 基于地理位置的路由协议当然需要进行定位
定位协议可以大致被分为一下两类:
- Range-based localization:需要具有准确位置信息的 beacon 节点,剩余节点的位置信息通过计算它们与某几个 beacon 节点的距离估计得出
- Range-free localization:其他节点的位置信息并不依靠测距计算
Ranging Techniques
Received Signal Strength (RSS)
RSS 是最常用的测距手段,它会测量接收到的信号强度,并根据信号强度随距离增加而衰减这一事实,估计出距离,具体来说,它会使用到:
- 接收信号的功率
- 传输功率
- 路径损失模型
beacon 节点会周期性的广播 beacon 消息,来估计它与其他节点的距离。
但是 RSS 的准确度会受到阴影效应以及多径传输的影响,且当遇到 None line of sight(NLoS)的场景时,距离的估测错误可能会更严重。
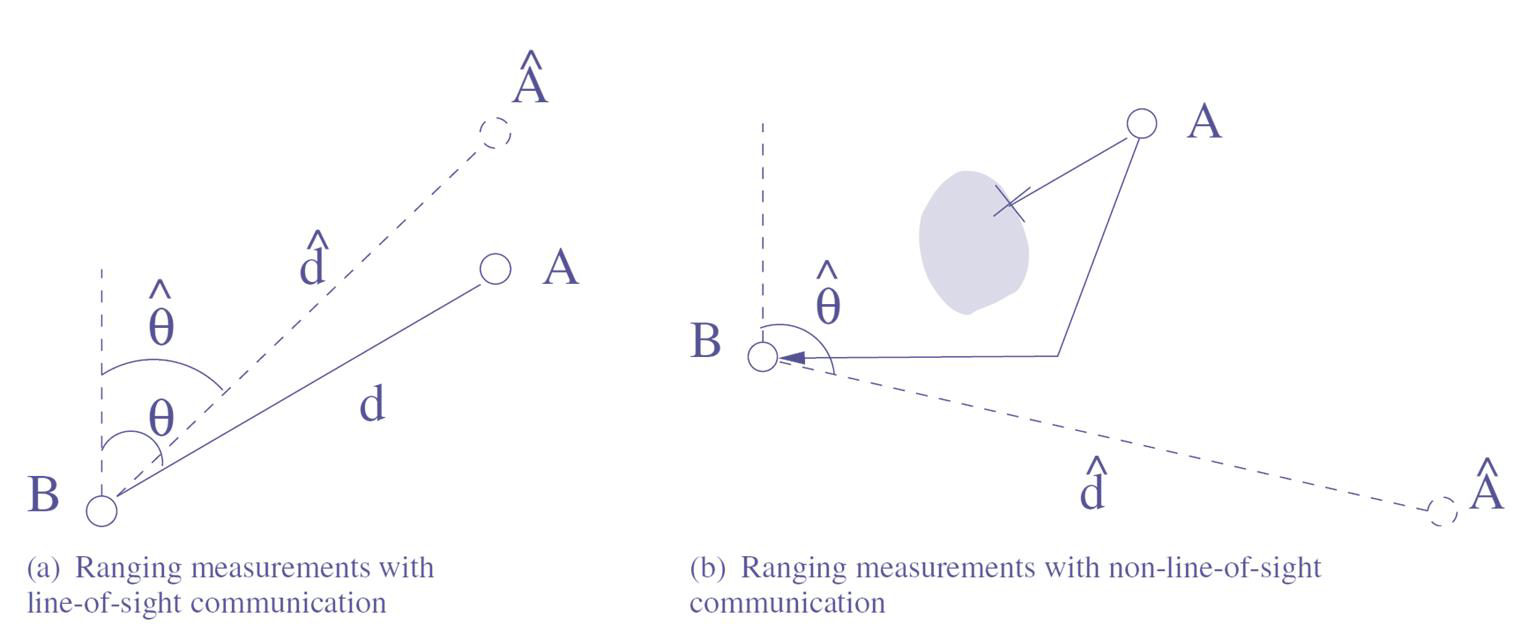
Time of Arrival (ToA)
ToA 依赖于对信号在两个节点之间传输时间的准确度量,之后距离会根据传输时间以及信号速度进行计算。这就涉及到同步技术了,两个节点需要保持时钟同步。我们有两种方式来测算传输时间:
One-way ToA:
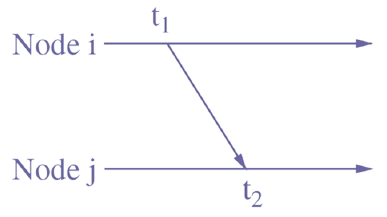
d i s t i j = ( t 2 − t 1 ) × v {\rm dist}_{ij}=(t_2-t_1)\times v distij=(t2−t1)×v
需要发端与收端的时钟高度同步。
Two-way ToA: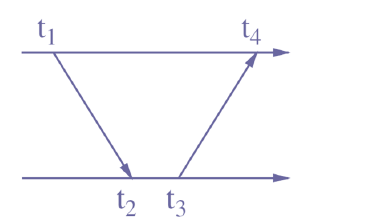
d i s t i j = ( t 4 − t 1 ) − ( t 3 − t 2 ) 2 × v {\rm dist}_{ij}=\frac{(t_4-t_1)-(t_3-t_2)}{2}\times v distij=2(t4−t1)−(t3−t2)×v
收端和发端并不需要进行时钟同步,但发端需要发送一个额外消息来告知收端咱俩之间的位置。
ToA 方法需要保证对传输时间的精确度量,否则,由于 RF 信号在空气中传播速度非常快,一点小的误差也会对计算结果产生很大影响。
Time Difference of Arrival (TDoA)
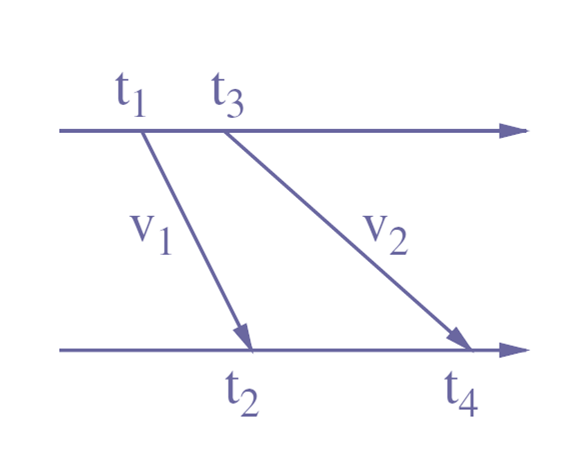
和 ToA 不同的是,TDoA 会使用两个信号,且这两个信号的传播速度不同。
d i s t i j = ( v 1 − v 2 ) × ( t 4 − t 2 − t w a i t ) {\rm dist}_{ij}=(v_1-v_2)\times (t_4-t_2-t_{wait}) distij=(v1−v2)×(t4−t2−twait)
其中, t w a i t t_{wait} twait 是两个信号发送的间隔时间。很明显,TDoA 并不需要发端和收端的同步。但由于需要发送不同传播速度的信号,可能需要添加额外的硬件设备。Angle of Arrival (AoA)
AoA 依据接收信号的方向来进行定位,接收信号的方向通常依靠定向天线(directional antennas)或者特定的多天线阵列来进行估测。
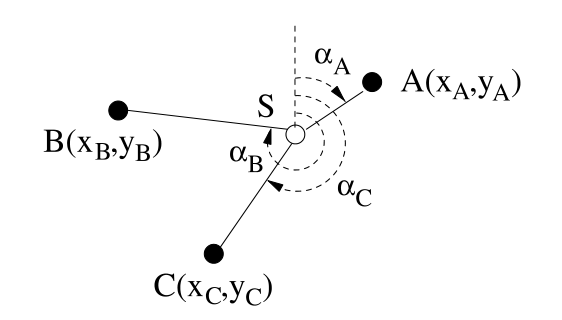
上图中,位置信息未知的节点 S 收到了三个 beacon 节点的 beacon 信号,它会估计每个 beacon 的 AoA, α A \alpha _A αA, α B \alpha _B αB, α C \alpha _C αC。
但 AoA 的准确测量需要高复杂度的天线阵列,这会造成很大开销。而且天线阵列需要在空间位置上分散开来,对于尺寸尽可能小的传感器节点来说不是很可行。而且 NLoS 对 AoA 的影响甚至比 RSS 还要严重。
Range-Based Localization Protocols
Triangulation

如果使用的是 AoA,那么在节点 S 处的关于两个 beacon 节点的 AoA 可以被用来进行定位。两个 beacon 节点和 S 构成了一个三角形,借助于三角形的几何性质,我们可以很容易的得出节点 S 的位置。
Trilateration
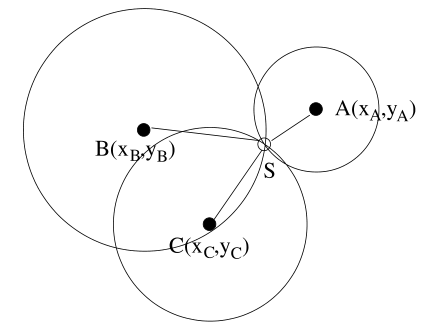
如果我们已经测出节点 S 和它邻居节点(或者这里可以叫做 anchor)的距离,那么,传感器的位置一定位于在以 anchor 位置为圆心,半径等于传感器和 anchor 距离的圆周上的某处。在二维空间中,通过至少三个这样的 anchor,我们就可以唯一确定一个节点 S 的位置。
Iterative and Collaborative Multilateration
Iterative Multilateration:
在 Trilateration 中我们至少需要 3 个 anchor 来唯一确定一个位置,但该方法也可以推广到无需 3 个 anchor 的情况。
如果某个节点通过 Trilateration 得到自己的位置之后,它自己会变成一个 anchor,并且将包含自己位置的 anchor 信息广播出去。这个迭代过程会一直持续下去,直到所有节点的位置信息都被得出。
但迭代方法的一个问题在于,如果某次 Trilateration 计算的位置不精确,那么这个不精确会在之后的迭代中不断积累,也就是越算越离谱。
Collaborative Multilateration:
如果某个节点的 anchor 没有到达三个,那么它可以通过多跳通信来获得额外的 anchor 位置信息。
Security
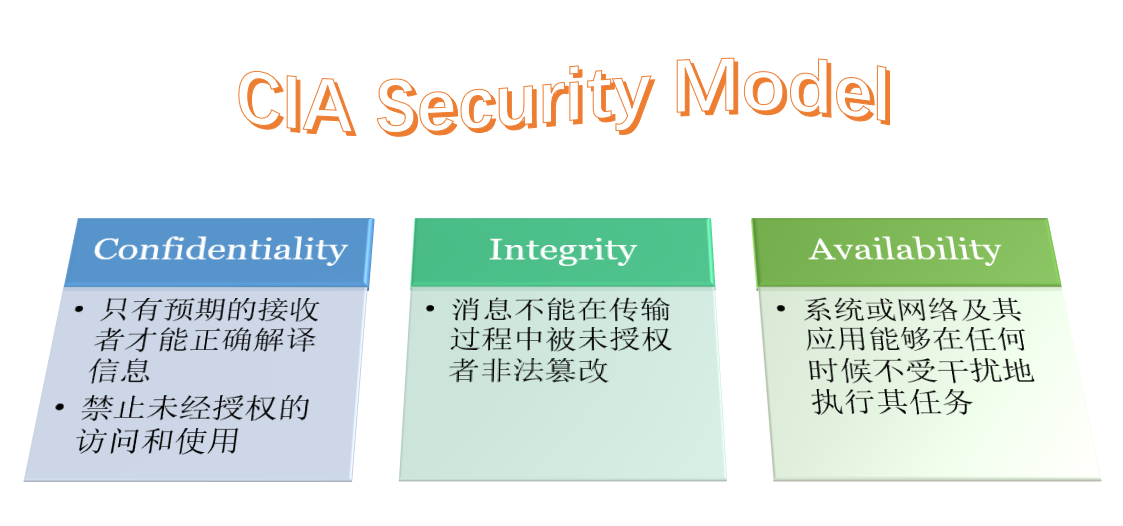
Challenges of Security in WSNs
Resource constraints
许多安全机制需要非常昂贵的计算代价,或者需要与其他节点或 "设备 "进行通信(例如用于授权目的),从而导致了大量的能源开销。这对于有限存储资源的传感器节点来说是绝对承受不起的。
Lack of central control
由于传感器网络的大规模、资源限制和网络动态性,在传感器网络中设立一个中央控制点往往是不可行的。因此,安全机制应该是去中心化的,依靠节点之间的协作来实现。
Remote location
防止安全攻击的第一道防线是为传感器节点提供可控的物理访问。但许多 WSN 无人看管,因为它们运行在人迹罕至的地方,部署在对公众开放的环境中,而且由于规模太大,连续监测和保护传感器节点免受攻击很难做到。
这些挑战使得防止未经授权的物理访问和检测传感器设备的篡改变得非常困难,特别是由于许多传感器节点的低成本,一些先进(和昂贵)的保护措施可能无法实施。
Error prone communication
WSN 中的数据包可能由于各种原因而丢失或损坏,包括信道错误、路由问题和冲突。安全机制可能无法分辨这是由于本身的通信错误引起的还是非法攻击造成的。
Time Synchronization
在分布式系统中,每个节点都有自己的时钟和自己的时间概念。然而,传感器节点之间的时钟同步是很重要的:
- 识别真实世界某个物理事件的因果关系
- 清除冗余的传感器数据
基于硬件振荡器的计算机时钟是所有计算设备的重要组成部分。一个典型的时钟由一个石英稳定振荡器(quartz-stabilized oscillator)和一个计数器组成,该计数器随着石英晶体的每一次振荡而被递减。每当计数器的值达到 0 时,它就被重置为原来的值,并产生一个中断。每个中断都会使软件时钟递增(另一个计数器),应用程序可以使用合适的应用编程接口读取和使用该时钟。
软件时钟为传感器节点提供了一个本地时间,其中 C ( t ) C(t) C(t) 表示在某个实际时间 t t t 的时钟读数。
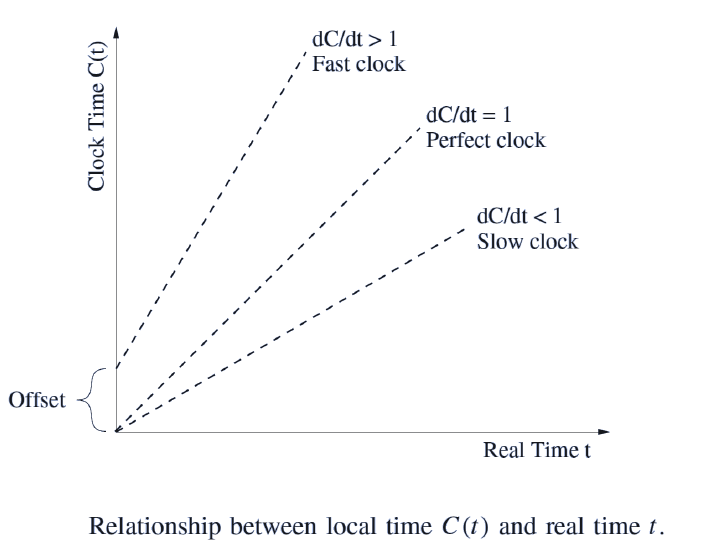
大多数现有的时间同步协议都是基于 pairwise synchronization,两个节点使用至少一个同步消息 (synchronization message) 来同步它们的时钟。
通过在多个节点对之间重复这一过程,可以实现 Network wide synchronization,直到网络中的每个节点都能够调整其时钟为止。
我们介绍两种同步消息的类型:
- One Way Message Exchange
- Two Way Message Exchange
One Way Message Exchange

节点 i i i 在自己时钟的 t 1 t_1 t1 时刻向节点 j j j 发送一个同步消息,同步消息中带有这个时间戳 t 1 t_1 t1。节点 j j j 在自己时钟的 t 2 t_2 t2 时刻收到了同步消息。因此两个时钟的 offset 可计算为
t 2 − t 1 = D + δ t_2-t_1=D+\delta t2−t1=D+δ
其中,传播时间 D D D 通常很短,经常可以忽略,或者假设为一个常数值。Two Way Message Exchange
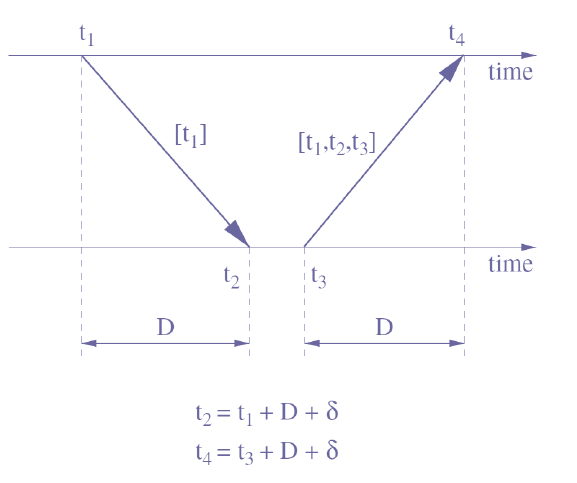
理解了上面 Two-way ToA 的朋友再看这个 Two Way Message Exchange 就会觉得非常熟悉了。传输时间 D D D 还是可以一样的计算为
D = ( t 4 − t 1 ) − ( t 3 − t 2 ) 2 D=\frac{(t_4-t_1)-(t_3-t_2)}{2} D=2(t4−t1)−(t3−t2)然后根据 One Way Message Exchange 中提到的 offset 计算原理,我们可以根据 t 2 = t 1 + D + δ t_2=t_1+D+\delta t2=t1+D+δ 如下计算 offset:
δ = ( t 2 − t 1 ) − ( t 4 − t 3 ) 2 \delta=\frac{(t_2-t_1)-(t_4-t_3)}{2} δ=2(t2−t1)−(t4−t3)这表示收端的时钟比发端快多少,如果结果是负数,那么说明发端的时钟比收端快。
References
[1] Chapter 11 & 12, Wireless Sensor Networks by Ian F Akyildizand and Mehmet C Vuran.
[2] Chapter 9 & 10, Fundamentals of Wireless Sensor Networks: Theory and Practice by W. Dragie and C. Poellabauer. -
相关阅读:
【云原生之k8s】kubernetes核心组件
MFC 与 QT“常用控件”对比
蓝桥杯刷题
Java新手小白入门篇 Java面向对象(六)
搭建虚拟通道
LeetCode75——Day8
SpringSecurity(六)【自定义认证案例】
thinkCMF6 更改站点信息注意事项
性能测试监控指标及分析调优 | 京东云技术团队
1032 Sharing
- 原文地址:https://blog.csdn.net/myDarling_/article/details/128091196