Python解题 - CSDN周赛第11期 - 圆桌请客（脑筋急转弯）

本来想着没有all pass就不写题解了，但在赛后对最后一题纠结了好久，然后发现是个类似脑筋急转弯的题，自己与正确答案只差一层纸，实在有点不吐不快。另外本期考了经典的背包问题的模板题，也值得记录下来，加深记忆。

先表扬一下CSDN的进步：

• 后面两道难度较高的题目增加了“提示”内容，解释了示例中的答案是怎样计算的，帮助各位选手尽快理解题意。（虽然问哥还是花了不少时间阅读理解。。。）

再谈谈不足：

1. 第三题竟然出现在当天的每日一练里，也就是说，如果我起得早，把每日一练做了，就会在几个小时后开始的比赛中遇见刚刚做过的题。。。若不是故意的，只能说“比赛”和“每日一练”这两个子版块的工作人员相互之间沟通太少，或者每日一练的选题纯粹就是随机事件，没有人工核查。不过也无所谓，反正这题也是模板题。
2. 如果CSDN鼓励大家多多使用每日一练，就应该把用户体验做得好一点，排版太丑就不说了，各有所爱，关键问哥经常会遇到如果在纸上演算，或者本地窗口调试程序，而把每日一练的窗口晾上十几分钟后，再切回来就提示“权限不足”、“登录异常”，要求重新登录，而有时候还必须关闭浏览器才能再次打开，这实在是太不爽了。不知道这是不是只是我遇到的问题。

---

第一题：圆小艺

最近小艺酱渐渐变成了一个圆滑的形状——球！！小艺酱开始变得喜欢上球！小艺酱得到个同心圆。小艺酱对着个同心圆进行染色。相邻的圆范围内不能有相同的颜色。相隔一层的圆颜色相同。小艺酱想知道圆最外层的那种颜色全部染了多少？

分析

“全部染了多少”。。。加上“面积”两个字这么难吗？可能问哥的阅读理解一直比较弱，看完题目的第一反应竟是计算周长，而更加崩溃的是，题目给出的两个示例，如果使用周长计算的话，得出的结果和正确答案是一样的！于是单单在这第一道题上，问哥就因为阅读理解不过关（嗯，题目没有错-_-|）浪费了十几分钟。

在仔细又读了N遍题目以后，问哥才意识到这是要计算圆环。好吧，简单的数学题。

同心圆如下图所示，我们要求从最外层算起颜色相同的圆环的总面积。

圆环的面积 = 外圆的面积 - 内圆的面积，这自然不用说，使用步长为2的遍历即可，不过此题有个稍微需要注意的地方就是，圆的数量如果是奇数，最里面的圆的面积是要完整加进结果的，所以，为了代码的一致性，当n为奇数的时候，我们可以在最里面添加一个半径为0的“圆”，这样最后一个圆的面积减去0，就等于完整的面积了。

参考代码

def solution(n, arr):
    from math import pi
    a = sorted(arr,reverse=True)
    if n%2: a.append(0)
    result = 0
    for i in range(0,n,2):
        result += pi*(a[i]**2-a[i+1]**2)
    return f"{result:.3f}"

另外还有下面几个小坑：

1. 题目输入的圆的半径数组arr是无序的，所以第一步还要先对其进行排序，推荐倒序排序，这样在尾部添加一个半径为0的圆的时间复杂度是常数级。不过单就此题而言，正序倒序区别不大。
2. 圆周率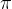的取值要尽量精确，否则可能出现结果误差。Python直接导入内置math模块的pi即可。
3. 最后别忘记要严格返回小数点后3位，即使最后结果得到的是一个整数，也要返回xx.000

---

第二题：K皇把妹

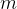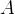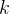存在个节点，目标节点在。每个节点有自己的权值。在权值内（含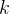值）选择一个权值非0节点且与目标节点距离最近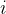。节点与节点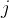的距离为。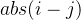

分析

这题就是字面意思，也比较好懂。要找符合要求的最近的节点，于是从节点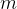使用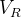、两个指针同时向左、右进行遍历即可。从1开始依次增加距离，找到符合条件（非0、小于等于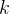）的节点即中断遍历、返回距离。

参考代码

def solution(n, m, k, arr):
    if n==1: return 0
    res = 1
    while True:
        r = m+res-1
        l = m-res-1
        if r
            if arr[r]!=0 and arr[r]<=k:
                return res
        if l>=0:
            if arr[l]!=0 and arr[l]<=k:
                return res
        res += 1

当然，极端情况只有1个节点的时候，距离为0。 

---

第三题：筛选宝物

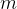已知存在个宝物，每个宝物都有自己的质量和价值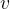，在考虑选择宝物时只能选择总质量小于等于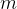的方案，请问在最优方案下选择宝物，能获取到最大价值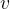是多少？

分析

经典模板背包基础题，经典到问哥只要复制以前回答别人的问答答案就好：

假设宝物/物品数量为3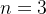（），能选择的总质量（背包容量）最高6公斤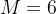（），则可列出动态规划表如下：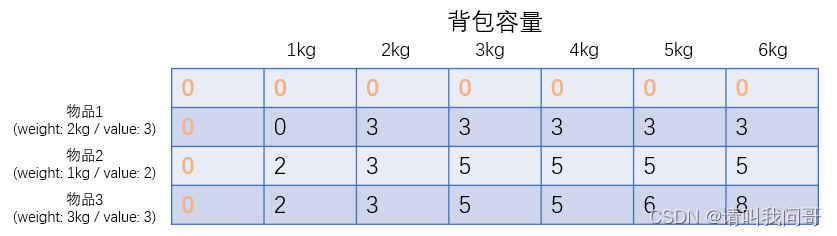

首先先创建一个(0 to 3, 0 to 6) 的二维数组，默认全为0（表示背包里面什么都没有），使用指针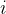和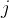分别表示上表的横、纵坐标。由于本题默认的答题模板里使用的是vector二维数组来保存了宝物的重量和价值，所以 就表示了第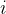个宝物的重量，而 则表示了第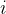个宝物的价值。然后就可以开始状态转移进行填表的操作了：

1. 当背包容量只有1公斤，而我只有物品1（）的时候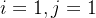，。物品1的重量为2公斤（），所以啥也放不了， 的价值就等于上一行（注意：状态转移是由左向右、自上而下）的 的价值，也就是0；
2. 当背包容量为2公斤，而我只有物品1的时候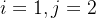，。正好可以放下物品1，所以最大价值为3（）；
3. 当背包容量大于2公斤，而我只有物品1，最大价值都为物品1的价值，所以 到  的最大价值都是3（从 转移而来）。

第一层转移完毕，然后考虑物品2（）：

1. 当背包容量只有1公斤，而我有物品1和物品2的时候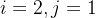，。因为物品2的重量为1公斤，所以只能放物品2， 的价值就等于上一行 的价值（0，表示不放物品2），和放了物品2（ 表示背包容量减去当前物品的容量，大于等于0则表示能放下当前物品，所以价值为当前物品的价值）二者相比较取大的那个：物品2的价值2。
2. 当背包容量为2公斤，而我有物品1和物品2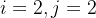，。要么放物品1，要么放物品2，不能同时放，所以同上面的比较过程，放入物品1的价值最大，所以 为3。
3. 当背包容量为3公斤，而我有物品1和物品2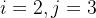，。可以同时放物品1和物品2（ 为放了当前物品后背包剩余的容量，而之前已经计算过剩余容量的最大价值为3，也就是物品1的价值），所以经过比较， 为二者价值之和，也就是5。
4. 当背包容量大于3公斤的推导过程同上。

第二层转移完毕，而由此我们也可以推出状态转移方程：

拥有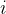种宝物、质量为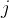的最大价值 = （如果放不下当前的宝物，则等于其余宝物质量为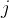的最大价值）或者（如果放得下当前宝物，就等于不放当前宝物、只放其余宝物的质量为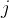的最大价值 与 放了当前宝物后，剩下的质量对应的最大价值，二者较大的一个）

。。。描述得忒费劲，翻译成代码就比较清楚了：

参考代码

def solution(n, M, vector):
    dp = [[0]*(M+1) for _ in range(n+1)]
    for i in range(1,n+1):
        for j in range(1,M+1):
            if j-vector[i-1][0]>=0:
                dp[i][j] = max(dp[i-1][j],dp[i-1][j-vector[i-1][0]]+vector[i-1][1])
            else:
                dp[i][j] = dp[i-1][j]
    return dp[n][M]

---

第四题：圆桌

有N个客人与足够多张的圆桌。主人安排每位客人坐在一个圆桌边，但是每位客人希望自己左右边上分别有一些空座位，不然会觉得害羞。注意，如果一个客人所在的圆桌只有他一个人，那么他左边的空座位数量就是他右边的空座位数量。试问主人需要准备多少个座位，才能让每个客人舒适的坐下。

分析

“此题代码简单，但思维难度却不小。”

问哥看了别人的题解后，感觉本题更像是脑筋急转弯，想明白了，一点就通；而如果想不通，是很难找到解题方法的。

洛谷的原题，贪心算法，写的题解太多了（主要是想通了以后就太简单了）。问哥就不啰嗦了，简单来讲，就是假设所有人都围成一圈的话，尽量让要求左边空位多的人和要求右边空位多的客人相邻，然后取二者最大的空位数，该逻辑对一个客人单独一桌的情况同样成立。然后将所有两两组队的最大空位相加，最后再加上客人数即可。——这部分逻辑问哥一开始就明白了（当然还是浪费了二十分钟在阅读理解上-_-|），但是问哥比较难以想通的是，为什么一个客人的左边空位和右边空位可以拆开来单独进行排序？如果客人左右边空位的数量相差过大，他的左边配对了客人后，右边还能配对吗？介于比赛时间此时已所剩无几，问哥也没有继续求证下去，但是如果有时间画个图，就会清楚地发现：即使把左、右边空位拆开分别排序、组对，也一样、并且一定是可以配对成功的，很简单的道理：左边和右边，不管是多少，它们的数量恒等于人数。

举例：假设有5位客人A、B、C、D、E，对应的颜色以及对左右空位的要求（数字）如下，按照解题思路，将客人们左、右空位拆开，再进行排序后配对：

得到的结果一定可以围成一个圆（或多个圆，取决于排序后配对的位置）：

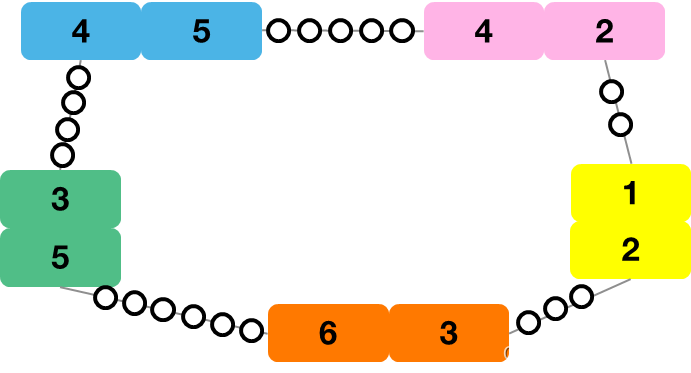
使用图论应该可以进行数学上的证明，但是问哥数学底子薄弱，就到此为止吧，明白意思就可以了，哈哈 :D

参考代码

def solution(n, vector):
    l, r = zip(*vector)
    l.sort(reverse=True)
    r.sort(reverse=True)
    res = 0
    for i in range(n):
        res += max(l[i],r[i])
    return res+n