代码随想录67——额外题目【动态规划】：5最长回文子串、132分割回文串II、673最长递增子序列的个数

1.5最长回文子串

参考：代码随想录，5最长回文子串；力扣题目链接

1.1.题目

1.2.解答

本题和 647.回文子串 差不多是一样的，但 647.回文子串 更基本一点，建议可以先做647.回文子串。

动规五部曲：

1.确定dp数组（dp table）以及下标的含义

布尔类型的dp[i][j]：表示区间范围[i,j] （注意是左闭右闭）的子串是否是回文子串，如果是dp[i][j]为true，否则为false。

2.确定递推公式

在确定递推公式时，就要分析如下几种情况。

整体上是两种，就是s[i]与s[j]相等，s[i]与s[j]不相等这两种。

• 当s[i]与s[j]不相等，那没啥好说的了，dp[i][j]一定是false。

• 当s[i]与s[j]相等时，这就复杂一些了，有如下三种情况

（1）情况一：下标i 与 j相同，同一个字符例如a，当然是回文子串
（2）情况二：下标i 与 j相差为1，例如aa，也是文子串
（3）情况三：下标：i 与 j相差大于1的时候，例如cabac，此时s[i]与s[j]已经相同了，我们看i到j区间是不是回文子串就看aba是不是回文就可以了，那么aba的区间就是i+1与 j-1区间，这个区间是不是回文就看dp[i + 1][j - 1]是否为true。

以上三种情况分析完了，那么递归公式如下：

if (s[i] == s[j]) {
    if (j - i <= 1) { // 情况一 和 情况二
        dp[i][j] = true;
    } else if (dp[i + 1][j - 1]) { // 情况三
        dp[i][j] = true;
    }
}
1
2
3
4
5
6
7

注意这里没有列出当s[i]与s[j]不相等的时候，因为在下面dp[i][j]初始化的时候，就初始为false。

在得到[i,j]区间是否是回文子串的时候，直接保存最长回文子串的左边界和右边界，代码如下：

if (s[i] == s[j]) {
    if (j - i <= 1) { // 情况一 和 情况二
        dp[i][j] = true;
    } else if (dp[i + 1][j - 1]) { // 情况三
        dp[i][j] = true;
    }
}
if (dp[i][j] && j - i + 1 > maxlenth) {
    maxlenth = j - i + 1;
    left = i;
    right = j;
}
1
2
3
4
5
6
7
8
9
10
11
12

3.dp数组如何初始化

dp[i][j]可以初始化为true么？ 当然不行，怎能刚开始就全都匹配上了。

所以dp[i][j]初始化为false。

4.确定遍历顺序

首先从递推公式中可以看出，情况三是根据dp[i + 1][j - 1]是否为true，在对dp[i][j]进行赋值true的。dp[i + 1][j - 1] 在 dp[i][j]的左下角，如图：

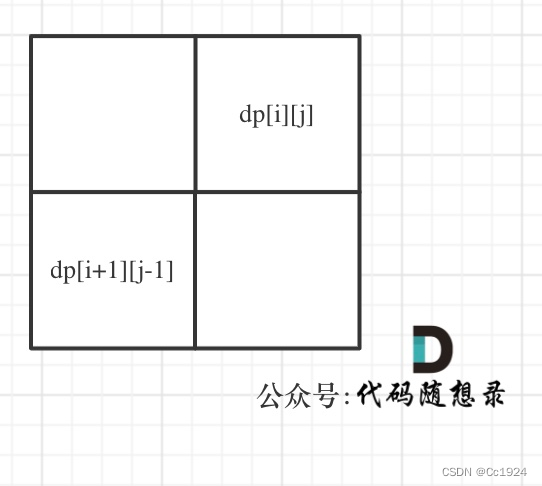
所以一定要从下到上，从左到右遍历，这样保证dp[i + 1][j - 1]都是经过计算的。

有的代码实现是优先遍历列，然后遍历行，其实也是一个道理，都是为了保证dp[i + 1][j - 1]都是经过计算的。

5.举例推导dp数组

举例，输入：“aaa”，dp[i][j]状态如下：

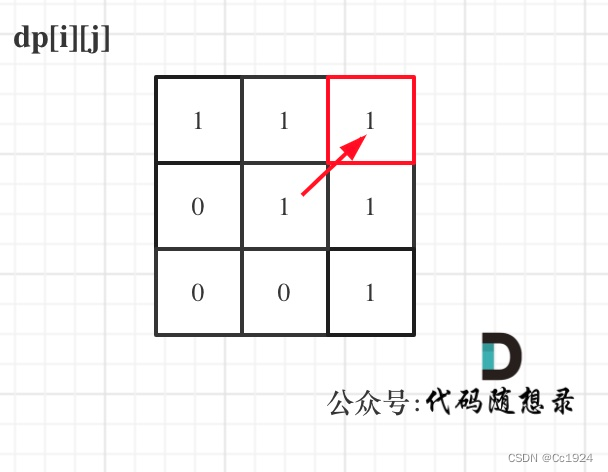
最后给出整体代码如下：

string longestPalindrome(string s)
{
    // 1.定义dp数组并初始化为false
    vector<vector<bool>> dp(s.size(), vector<bool>(s.size(), false));
    int max_len = 0;   // 最长回文子串的长度
    int left = 0;
    int right = 0;

    // 2.开始动态规划：从下往上、从左往右进行遍历
    for(int i = s.size()-1; i >= 0; i--)
    {
        for(int j = i; j < s.size(); j++)
        {
            // 2.1.不相等：则肯定就是false
            if(s[i] != s[j])
            {
                dp[i][j] = false;   // 这一句不加也行
            }
            // 2.2.相等：则要分情况讨论
            else
            {
                if(i == j)   // 一个字符长度，是回文
                    dp[i][j] = true;
                else if(j - i == 1)  // 两个字符，也是回文
                    dp[i][j] = true;
                else
                    dp[i][j] = dp[i+1][j-1];  // 取决于内部的字符
            }

            // 如果是回文串，计算是否是最大长度的子串
            if(dp[i][j] && j-i+1 > max_len)
            {
                max_len = j - i + 1;
                left = i;
                right = j;
            }
        }
    }

    // 截取最长回文子串返回：开始位置，长度
    return s.substr(left, right-left+1);    
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42

2.132分割回文串II

参考：代码随想录，132分割回文串II；力扣题目链接

2.1.题目

2.2.解答

关于回文子串，两道题目题目是一定要掌握的。

• 647.回文子串
• 5.最长回文子串，这道题和 647.回文子串 基本一样的

这两道题目是回文子串的基础题目，本题也要用到相关的知识点。

动规五部曲分析如下：

1.确定dp数组（dp table）以及下标的含义

dp[i]：范围是[0, i]的回文子串，最少分割次数是dp[i]。

2.确定递推公式

来看一下由什么可以推出dp[i]。

• 首先如果长度为[0, i]的子串本身就是回文串了，那么本着要求最少分割的回文串的目的出发，显然就不需要对它进行分割了，所以它的最少分割次数为0

• 如果要对长度为[0, i]的子串进行分割，分割点为j。讨论如下：

如果分割后，区间[j + 1, i]是回文子串，那么dp[i] 就等于 dp[j] + 1。

这里可能有同学就不明白了，为什么只看[j + 1, i]区间，不看[0, j]区间是不是回文子串呢？

那么在回顾一下dp[i]的定义： 范围是[0, i]的回文子串，最少分割次数是dp[i]。

[0, j]区间的最小切割数量，我们已经知道了就是dp[j]。

此时就找到了递推关系，当切割点j在[0, i] 之间时候，dp[i] = dp[j] + 1;

本题是要找到最少分割次数，所以遍历j的时候要取最小的dp[i]。

所以最后递推公式为：dp[i] = min(dp[i], dp[j] + 1);

注意这里不是要 dp[j] + 1 和 dp[i]去比较，而是要在遍历j的过程中取最小的dp[i]！

可以有dp[j] + 1推出，当[j + 1, i] 为回文子串

3.dp数组如何初始化

• 首先来看一下dp[0]应该是多少。

dp[i]： 范围是[0, i]的回文子串，最少分割次数是dp[i]。

那么dp[0]一定是0，长度为1的字符串最小分割次数就是0。这个是比较直观的。

• 再看一下非零下标的dp[i]应该初始化为多少？

在递推公式dp[i] = min(dp[i], dp[j] + 1) 中我们可以看出每次要取最小的dp[i]。

那么非零下标的dp[i]就应该初始化为一个最大数，这样递推公式在计算结果的时候才不会被初始值覆盖！

如果非零下标的dp[i]初始化为0，在那么在递推公式中，所有数值将都是零。

代码如下：

vector<int> dp(s.size(), INT_MAX);
dp[0] = 0;
1
2

其实也可以这样初始化，更具dp[i]的定义，dp[i]的最大值其实就是i，也就是把每个字符分割出来。

所以初始化代码也可以为：

vector<int> dp(s.size());
for (int i = 0; i < s.size(); i++) dp[i] = i;
1
2

4.确定遍历顺序

根据递推公式：dp[i] = min(dp[i], dp[j] + 1);

j是在[0，i]之间，所以遍历i的for循环一定在外层，这里遍历j的for循环在内层才能通过 计算过的dp[j]数值推导出dp[i]。

代码如下：

for (int i = 1; i < s.size(); i++) {
    if (isPalindromic[0][i]) { // 判断是不是回文子串
        dp[i] = 0;
        continue;
    }
    for (int j = 0; j < i; j++) {
        if (isPalindromic[j + 1][i]) {
            dp[i] = min(dp[i], dp[j] + 1);
        }
    }
}
1
2
3
4
5
6
7
8
9
10
11

大家会发现代码里有一个isPalindromic函数，这是一个二维数组isPalindromic[i][j]，记录[i, j]是不是回文子串。

所以先用一个二维数组来保存整个字符串的回文情况，这个和前面做的 5.最长回文子串 的题目是一样的。

代码如下：

vector<vector<bool>> isPalindromic(s.size(), vector<bool>(s.size(), false));
for (int i = s.size() - 1; i >= 0; i--) {
    for (int j = i; j < s.size(); j++) {
        if (s[i] == s[j] && (j - i <= 1 || isPalindromic[i + 1][j - 1])) {
            isPalindromic[i][j] = true;
        }
    }
}
1
2
3
4
5
6
7
8

5.举例推导dp数组

以输入："aabc" 为例：

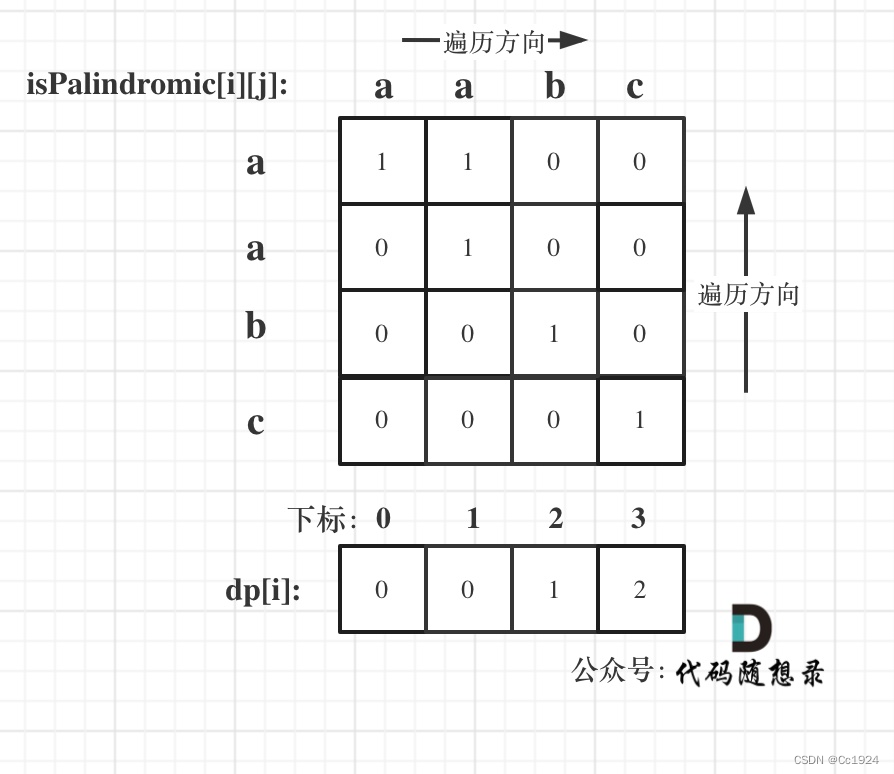
最后给出代码如下：

int minCut(string s)
{
    // 1.先把所有子串是不是回文判断出出来
    vector<vector<bool>> is_pal(s.size(), vector<bool>(s.size(), false));
    for(int i = s.size()-1; i >= 0; i--)
        for(int j = i; j < s.size(); j++)
            if(s[i] == s[j] && (j-i <= 1 || is_pal[i+1][j-1]))
                is_pal[i][j] = true;
        
    // 2.定义dp数组并初始化：初始化成最大值，这样后面递推公式才能有效
    vector<int> dp(s.size(), 0);
    for(int i = 1; i < s.size(); i++)
        dp[i] = i; 

    // 3.动态规划
    for(int i = 1; i < s.size(); i++)
    {
        if(is_pal[0][i] == true)
        {
            dp[i] = 0;
            continue;
        }

        for(int j = 0; j < i; j++)
            if(is_pal[j+1][i])
                dp[i] = min(dp[i], dp[j] + 1);
    } 

    return dp[s.size()-1];
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

3.673最长递增子序列的个数

参考：代码随想录，673最长递增子序列的个数；力扣题目链接

3.1.题目

3.2.解答

TODO：比较复杂，等待二刷。。。