平衡搜索树——红黑树小记

红黑树

定义

红黑树是一种 “平衡” 二叉 搜索树
“平衡”: 相比较于AVL树来说，是一种弱平衡
在红黑树中，任意从根到叶子的路径中，LEN(最长的路径)<= 2*LEN(最短的路径)

规则

1. 红黑树中的结点:或红或黑
2. 红黑树的根一定是黑色的
3. 红黑树的“叶子结点”一定是黑色的。（此处的叶子: node == null）
4. 红黑树中，任意路径(从根到叶子)，红色不能和红色相邻
5. 红黑树中，任意路径(从根到叶子)，上面黑色结点的数量必须一样多

操作规则

查找操作:同普通的搜索树规则
插入操作:碰瓷“红色不能和红色相邻”这条规则——新插入的结点，一定是红色的
1.按照普通搜索树方式插入
2.判断是否破坏了红色不能红色相邻的规则，如果破坏了，则进行平衡调整操作
3.将根置为黑色

平衡调整规则

假设：新插入的结点(node)破坏了“红色不能相邻”的规则，且：

node的父节点: parent
node 的祖父结点: grandpa
node的叔叔结点: uncle(假如存在)

其中，node既可能是新插入的结点，也可能是不断向根回溯过程中的"grandpa"

根据红黑树定义及规则可知，以下成立：

• parent一定存在，且一定是红色
• grandpa一定存在，且一定是黑色

规则

1. uncle存在 && uncle的颜色是红色

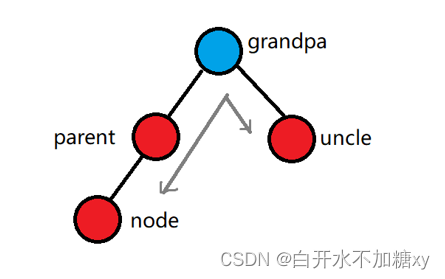
步骤:

1. parent的颜色=黑色 uncle的颜色=黑色
2. grandpa的颜色=红色
3. 把 grandpa视为node，重新循环进行再平衡的过程，直到回溯到根上为止

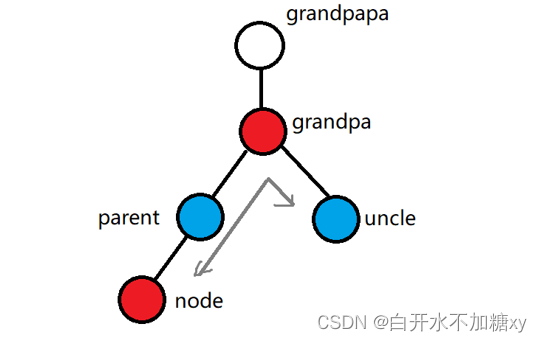
2.uncle 不存在或者(uncle存在&& uncle是黑色的)

(1) parent和grandpa的关系 与 node和parent的关系不一致

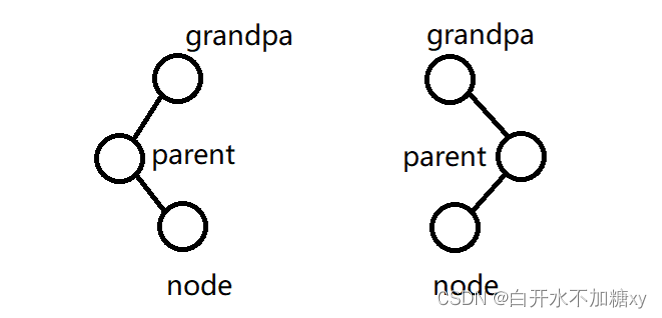
步骤

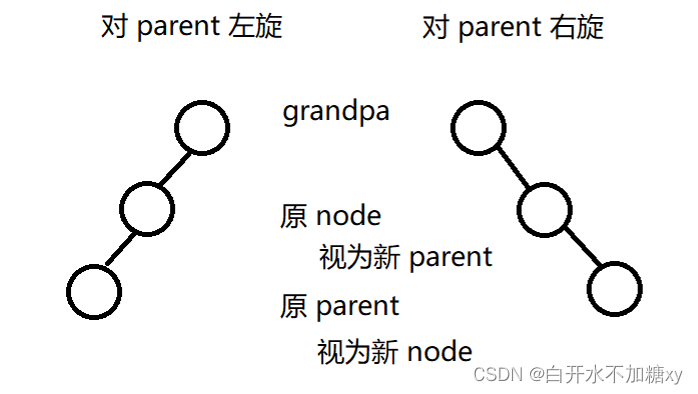
如果原来关系一致，不需要做此步骤。

3.关系一致后处理

优点

不改变路径上的黑色数量同时解决了parent和node红色相邻的问题

代码

插入

 /**
     * 保存红黑树的根结点
     */
    public RBTreeNode root = null;
    /**
     * 保存红黑树中的结点个数
     */
    public int size = 0;

    /**
     * 向红黑树中插入新的关键字
     * @param key 关键字
     * @return 是否插入成功
     * true: 插入成功
     * false: 插入失败（key 出现重复）
     */
    public boolean insert(long key) {
        // 1. 按照普通搜索树的方式进行插入
        if (root == null) {
            root = new RBTreeNode(key, null, BLACK);
            size++;
            return true;
        }

        RBTreeNode parent = null;
        RBTreeNode current = root;

        while (current != null) {
            if (key == current.key) {
                return false;
            } else if (key < current.key) {
                parent = current;
                current = current.left;
            } else {
                parent = current;
                current = current.right;
            }
        }

        /**
         * 根据插入规则，每次新插入的结点，一定是红色的
         */
        RBTreeNode node = new RBTreeNode(key, parent, RED);
        if (key < parent.key) {
            parent.left = node;
        } else {
            parent.right = node;
        }
        size++;

        /**
         * 进行红黑树规则的判断 + 平衡调整过程
         */
        adjustBalance(node);

        return true;
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57

平衡调整代码

private void adjustBalance(RBTreeNode node) {
        while (true) {
            RBTreeNode parent = node.parent;
            if (parent == null) {
                break;
            }

            if (parent.color == BLACK) {
                break;
            }

            /**
             * 一定破坏了"红色不能相邻"的规则
             */
            RBTreeNode grandpa = parent.parent;

            // 找到叔叔结点
            if (parent == grandpa.left) {
                RBTreeNode uncle = grandpa.right;
                if (uncle != null && uncle.color == RED) {
                    /**
                     * 情况1：叔叔存在 并且 叔叔的颜色是红色
                     * 步骤：
                     * 1. 叔叔和父亲的颜色改成黑色
                     * 2. 祖父的颜色改成红色
                     * 3. 把祖父视为 node，再去判断是否违反规则了
                     */
                    parent.color = uncle.color = BLACK;
                    grandpa.color = RED;
                    node = grandpa;
                    continue;
                } else {
                    // 判断 grandpa <-> parent 和 parent <-> node 的关系是否不一致
                    // 已知 parent 是 grandpa 的左边
                    if (node == parent.right) {
                        leftRotate(parent);

                        //swap(parent, node);
                        parent = node;
                    }

                    // 接下来统一处理关系一致的情况
                    rightRotate(grandpa);
                    grandpa.color = RED;
                    parent.color = BLACK;
                    break;
                }
            } else {
                RBTreeNode uncle = grandpa.left;
                if (uncle != null && uncle.color == RED) {
                    /**
                     * 情况1：叔叔存在 并且 叔叔的颜色是红色
                     * 步骤：
                     * 1. 叔叔和父亲的颜色改成黑色
                     * 2. 祖父的颜色改成红色
                     * 3. 把祖父视为 node，再去判断是否违反规则了
                     */
                    parent.color = uncle.color = BLACK;
                    grandpa.color = RED;
                    node = grandpa;
                    continue;
                } else {
                    // 判断 grandpa <-> parent 和 parent <-> node 的关系是否不一致
                    // 已知 parent 是 grandpa 的右边
                    if (node == parent.left) {
                        rightRotate(parent);

                        //swap(parent, node);
                        parent = node;
                    }

                    // 接下来统一处理关系一致的情况
                    leftRotate(grandpa);
                    grandpa.color = RED;
                    parent.color = BLACK;
                    break;
                }
            }
        }

        /**
         * 无论之前是什么情况，统一把根改成黑色
         * 走到此处时，root 一定不是 null
         */
        root.color = BLACK;
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86

左旋、右旋

与AVL树左旋右旋原理一致。可参考上篇博客中左旋调整平衡部分。

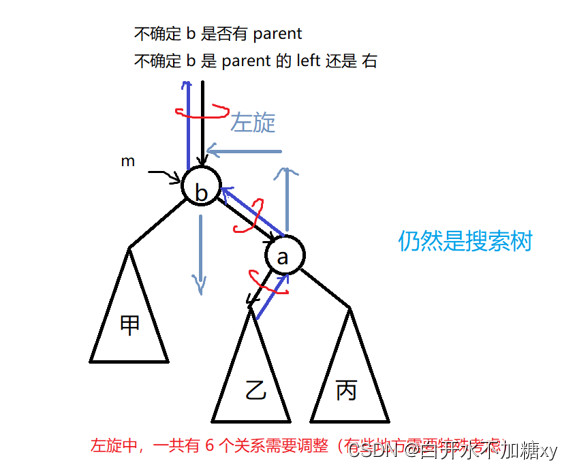
private void leftRotate(RBTreeNode m) {
        // m 代表图中的 b 结点
        // parent 代表 b 结点可能存在的父亲
        RBTreeNode parent = m.parent;
        // right 代表图中的 a 结点
        RBTreeNode right = m.right;
        // leftOfRight 代表图中的可能存在的乙子树的根结点
        RBTreeNode leftOfRight = right.left;
        /*
        其中: m != null && right != null
        但是: parent 不保证 !null, leftOfRight 不保证 !null
         */

        right.parent = parent;  // 蓝色线的关系
        // 黑色线的关系
        if (parent == null) {
            // m 是 root
            root = right;
        } else {
            if (m == parent.left) {
                parent.left = right;
            } else {
                parent.right = right;
            }
        }

        right.left = m; // 黑色线的关系
        m.parent = right;   // 蓝色线的关系

        m.right = leftOfRight;
        if (leftOfRight != null) {
            leftOfRight.parent = m;
        }
    }

    private void rightRotate(RBTreeNode m) {
        RBTreeNode parent = m.parent;
        RBTreeNode left = m.left;
        RBTreeNode rightOfLeft = left.right;

        left.parent = parent;
        if (parent == null) {
            root = left;
        } else {
            if (m == parent.left) {
                parent.left = left;
            } else {
                parent.right = left;
            }
        }

        left.right = m;
        m.parent = left;

        m.left = rightOfLeft;
        if (rightOfLeft != null) {
            rightOfLeft.parent = m;
        }
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59