与堆和堆排序相关的问题

与堆和堆排序相关的问题

作者：Grey

原文地址：

博客园：与堆和堆排序相关的问题

CSDN：与堆和堆排序相关的问题

堆结构说明

堆结构就是用数组实现的完全二叉树结构，

什么是完全二叉树？

每一层都是满的，或者即便不满，也是从左到右依次变满的

梳理一下一棵树是完全二叉树的可能性，对于一棵树的根节点 root：

• 如果左右树都是满二叉树，且左右树的高度一致，那么当前节点为根节点的树一定是满二叉树，当然也是完全二叉树。

• 如果左树是满二叉树，右树是完全二叉树，且左树比右树高度大1，那么当前节点为根节点的树是完全二叉树。

• 如果左树是满二叉树，右树是完全二叉树，且左右树的高度一致，此时当前节点为根节点的树也是完全二叉树。

• 如果左树是完全二叉树，右树是满二叉树，且左树高度比右树高度大1，此时当前节点为根节点的树也是完全二叉树。

除了上述四种可能性，其他情况下 root 为根节点的树都不是完全二叉树。

完全二叉树中如果每棵子树的最大值都在顶部就是大根堆；完全二叉树中如果每棵子树的最小值都在顶部就是小根堆。

Java 语言中的 java.util.PriorityQueue，就是堆结构。

因为是用数组表示完全二叉树，所以有如下两个换算关系，也就是堆的两种表示情况：

情况一，如果使用数组 0 号位置，那么对于 i 位置来说，它的：

• 左孩子下标：2 * i + 1

• 右孩子下标： 2 * i + 2

• 父节点下标： （i - 1）/ 2

情况二，如果不用数组 0 号位置，那么对于 i 位置来说，它的：

• 左孩子下标：2 * i 即：i << 1

• 右孩子下标：2 * i + 1 即：i << 1 | 1

• 父节点下标：i / 2 即：i >> 1

如果是小根堆（下标从 0 开始），

对每个元素 A[i]，都需要满足 A[i * 2 + 1] >= A[i] 和 A[i * 2 + 2] >= A[i]；

如果是小根堆（下标从 0 开始），

对每个元素 A[i]，都需要满足 A[i * 2 + 1] <= A[i] 和 A[i * 2 + 2] <= A[i]；

大根堆同理。

堆的数据结构定义如下，以大根堆为例，以下是伪代码

// 大根堆
public static class MyMaxHeap {
    // 用于存堆的数据
    private int[] heap;
    // 堆最大容纳数据的数量
    private final int limit;
    // 堆当前的容量
    private int heapSize;
    
    // 堆初始化
    public MyMaxHeap(int limit) {
      heap = new int[limit];
      this.limit = limit;
      heapSize = 0;
    }
    // 判断堆是否为空
    public boolean isEmpty() {
      return heapSize == 0;
    }
    // 判断堆是否满
    public boolean isFull() {
      return heapSize == limit;
    }
    public void push(int value) {
      // TODO 入堆
      // 注意：入堆后，也要保持大根堆的状态
    }
    public int pop() {
      // TODO 最大值出堆
      // 注意：出堆后，也要保持大根堆的状态
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

由上述数据结构定义可知，核心方法就是 push 和 pop，在每次操作后，要动态调整堆结构，使之保持大根堆的结构。

要完成这两个操作，就需要利用到堆的两个基本操作：

一个是 HeapInsert，一个是 Heapify。

Heapify 操作

Heapify 就是堆化的过程，以小根堆为例，示例说明

假设原始数组为：{3,2,1,4,5}，初始状态如下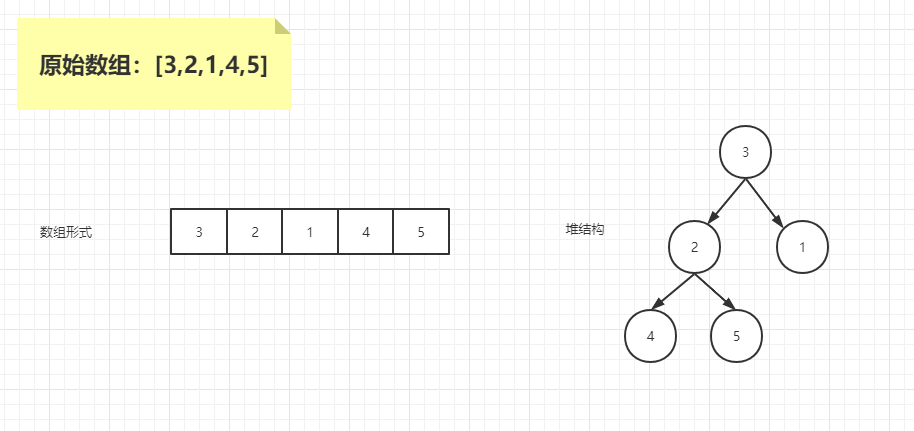

首先从头结点 3 开始，先找到 3 的左右孩子中较小的一个进行交换，现在较小的是右孩子 1，交换后是如下情况

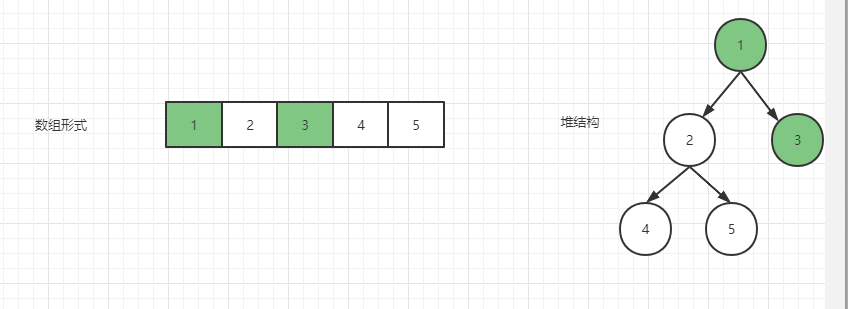
互换后，3 号结点已经没有左右孩子了，停止操作。

然后按顺序继续处理 2 结点，2 结点已经比左右孩子都小了，无需进行交换。

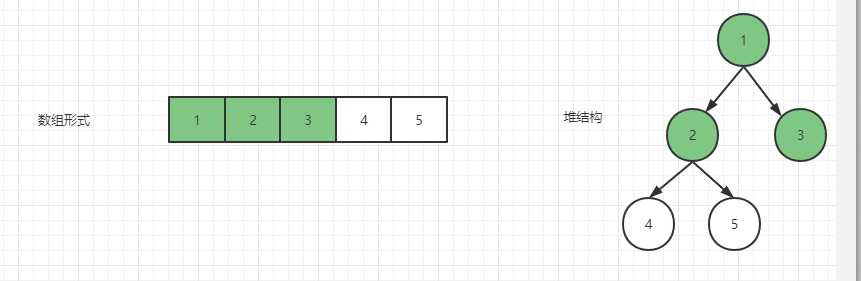
接下来是 4 结点和 5 结点，都没有左右孩子，就无需再做操作。

整个流程就是，每个结点（ 假设为 X ）去找自己的左右孩子中较小的那个（ 假设为 Y），然后 X 和 Y 交换位置，交换后，看 X 是否继续有孩子结点，往复这个过程，一直到整个二叉树遍历完成。

完整代码如下：

public class Solution {
  public static void heapify(int[] arr) {
    if (arr == null || arr.length <= 1) {
      return;
    }
    for (int i = arr.length - 1; i >= 0; i--) {
      heapify(arr, i, arr.length);
    }
  }
  private static void heapify(int[] arr, int i, int n) {
    int left = 2 * i + 1;
    while (left < n) {
      int min = left + 1 < n && arr[left + 1] < arr[left] ? left + 1 : left;
      if (arr[i] <= arr[min]) {
        break;
      }
      swap(arr, i, min);
      i = min;
      left = 2 * i + 1;
    }
  }

  private static void swap(int[] arr, int i, int j) {
    if (i != j) {
      arr[i] = arr[i] ^ arr[j];
      arr[j] = arr[i] ^ arr[j];
      arr[i] = arr[i] ^ arr[j];
    }
  }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

测评链接：LintCode 130 · Heapify

HeapInsert 操作

整个过程如下，以小根堆为例，从数组最后一个元素 X 开始，一直找其父节点 A，如果X 比 A 小，X 就和 A 交换，然后来到父节点 A，继续往上找 A 的父节点 B，如果 A 比 B 小，则把 A 和 B 交换……一直找到某个结点的头结点不比这个结点大，这个节点就可以停止移动了。以一个示例说明

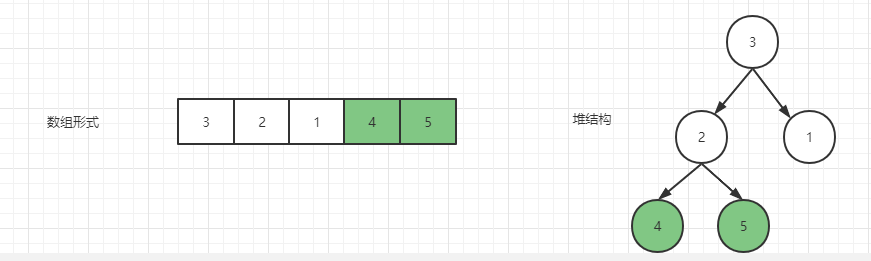
假设原始数组为：{3,2,1,4,5}，初始状态如下

从最后一个元素 5 开始，5 的父节点是 2，正好满足，无需继续往上找父节点，然后继续找倒数第二个位置 4 的父节点，也比父节点 2 要大，所以 4 节点也不需要动。

接下来是 1 结点，其父结点是 3 结点，所以此时要把 3 和 1 交换，变成如下样子

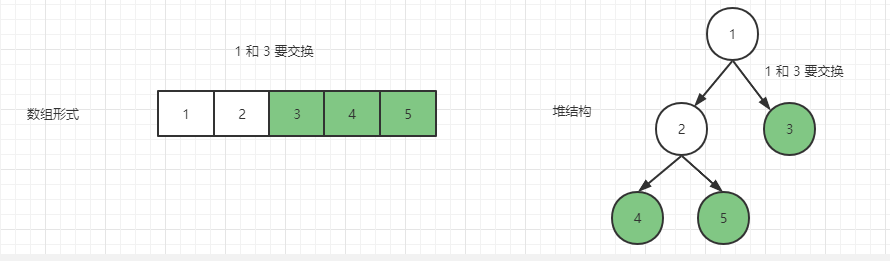
然后是 2 结点，2 结点的父节点 是 1 ，无需交换，然后是 1 结点，头结点，停止遍历，整个过程完毕。

HeapInsert 操作的完整代码如下

private void heapInsert(int[] arr, int i) {
    while (arr[i] > arr[(i - 1) / 2]) {
      // 一直网上找
      swap(arr, i, (i - 1) / 2);
      i = (i - 1) / 2;
    }
}
1
2
3
4
5
6
7

无论是 HeapInsert 还是 Heapify，整个过程时间复杂度是 O(logN)，N 是二叉树结点个数，其高度是 logN。

有了 Heapify 和 HeapInsert 两个过程，整个堆的 pop 操作和 push 操作都迎刃而解。

public void push(int value) {
  // 堆满了，不能入堆
    if (heapSize == limit) {
      throw new RuntimeException("heap is full");
    }
    // 把最后一个位置填充上，然后往小做 heapInsert 操作
    heap[heapSize] = value;
    // value  heapSize
    heapInsert(heap, heapSize++);
}

public int pop() {
    // 弹出的值一定是头结点
    int ans = heap[0];
    // 头结点弹出后，直接放到最后一个位置，然后往上做 heapify
    // 由于 heapSize 来标识堆的大小，heapSize--，就等于把头结点删掉了。
    swap(heap, 0, --heapSize);
    heapify(heap, 0, heapSize);
    return ans;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

堆排序

了解了 HeapInsert 和 Heapify 过程，堆排序过程，也就是利用了这两个方法，流程如下

第一步：先让整个数组都变成大根堆结构，建立堆的过程:

如果使用从上到下的方法，时间复杂度为$O(N\ast logN)$。

如果使用从下到上的方法，时间复杂度为$O(N)$。

第二步：把堆的最大值和堆末尾的值交换，然后减少堆的大小之后，再去调整堆，一直周而复始，时间复杂度为$O(N\ast logN)$。

第三步：把堆的大小减小成0之后，排序完成。

堆排序额外空间复杂度$O(1)$

堆排序完整代码如下

public class Code_HeapSort {

  public static void heapSort(int[] arr) {
    if (arr == null || arr.length < 2) {
      return;
    }
    // O(N*logN)
    //  for (int i = 0; i < arr.length; i++) { // O(N)
    //   heapInsert(arr, i); // O(logN)
    //  }
    // O(N)
    for (int i = arr.length - 1; i >= 0; i--) {
      heapify(arr, i, arr.length);
    }
    int heapSize = arr.length;
    swap(arr, 0, --heapSize);
    // O(N*logN)
    while (heapSize > 0) { // O(N)
      heapify(arr, 0, heapSize); // O(logN)
      swap(arr, 0, --heapSize); // O(1)
    }
  }

  // arr[index]刚来的数，往上
  public static void heapInsert(int[] arr, int index) {
    while (arr[index] > arr[(index - 1) / 2]) {
      swap(arr, index, (index - 1) / 2);
      index = (index - 1) / 2;
    }
  }

  // arr[index]位置的数，能否往下移动
  public static void heapify(int[] arr, int index, int heapSize) {
    int left = index * 2 + 1;
    while (left < heapSize) {
      int largest = left + 1 < heapSize && arr[left + 1] > arr[left] ? left + 1 : left;
      largest = arr[largest] > arr[index] ? largest : index;
      if (largest == index) {
        break;
      }
      swap(arr, largest, index);
      index = largest;
      left = index * 2 + 1;
    }
  }

  public static void swap(int[] arr, int i, int j) {
    int tmp = arr[i];
    arr[i] = arr[j];
    arr[j] = tmp;
  }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52

与堆排序相关的一个问题

题目描述

已知一个几乎有序的数组，几乎有序是指，如果把数组排好顺序的话，每个元素移动的距离一定不超过k，并且 k 相对于数组长度来说是比较小的，请选择一个合适的排序策略，对这个数组进行排序。(从小到大)

本题的主要思路就是利用堆排序：

先把 k 个数进堆，然后再加入一个，弹出一个（加入和弹出过程一定不会超过 k 次），最后堆里面剩下的继续弹出即可。

时间复杂度是$O(N\ast logK)$

完整代码如下

import java.util.Arrays;
import java.util.PriorityQueue;

public class Code_DistanceLessK {
  public static void sortedArrDistanceLessK(int[] arr, int k) {
    k = Math.min(arr.length - 1, k);
    PriorityQueue<Integer> heap = new PriorityQueue<>();
    int i = 0;
    for (; i < k + 1; i++) {
      heap.offer(arr[i]);
    }
    int index = 0;
    for (; i < arr.length; i++) {
      heap.offer(arr[i]);
      arr[index++] = heap.poll();
    }
    while (!heap.isEmpty()) {
      arr[index++] = heap.poll();
    }
  }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

更多

算法和数据结构学习笔记

算法和数据结构学习代码