力扣第73题

一、题目：73. 矩阵置零

二、题目解析：

解题步骤：注意题目要求原地算法–>利用矩阵的第一行和第一列记录矩阵需要置0的行和列，只要把0所在行和列的第一个位置置为0，然后再根据第一行和第一列0的位置，对矩阵置0即可

1. 定义两个boolean变量，遍历矩阵中第一行和第一列是否存在0，存在则置为true
2. 从二维数组中的第一行和第一列开始遍历是否存在0，存在则将当前元素所在行的第一个元素和所在列的第一个元素置为 0
3. 从二维数组中的第一行和第一列开始遍历，只要当前元素对应的第一行或第一列有一个元素为0，则将当前元素更新为 0
4. 最后根据两个boolean变量，判断是否需要将第一行和第一列置为0，需要则将该行或列置0即可

图示：

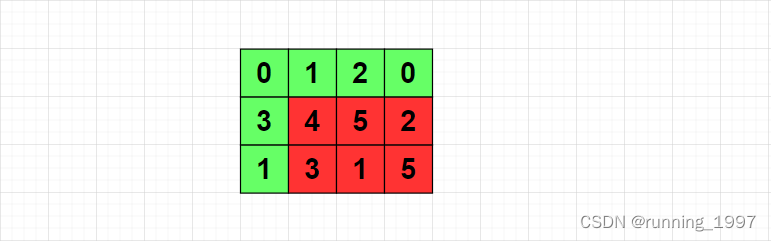
三、代码如下：

public int[][] setZero(int[][] matrix){
        int m = matrix.length;
        int n = matrix[0].length;
        boolean rowZero = false;
        boolean colZero = false;
        for(int i = 0;i < m; i++){
            //判断第一列是否存在0
            if(matrix[i][0] == 0){
                colZero = true;
            }
        }
        for (int j = 0 ;j < n; j++){
            //判断第一行是否存在0
            if(matrix[0][j] == 0){
                rowZero = true;
            }
        }
        for(int i = 1;i<m;i++){
            for(int j = 1; j<n;j++){
                if(matrix[i][j] == 0){
                    //如果当前元素等于 0，则将当前元素所在行的第一个元素和所在列的第一个元素置为 0
                    matrix[i][0] = matrix[0][j] = 0;
                }
            }
        }
        for(int i = 1;i<m;i++){
            for(int j = 1; j<n;j++){
                //只要当前元素对应的第一行或第一列有一个元素为0，则将当前元素更新为 0
                if(matrix[i][0] == 0 || matrix[0][j] ==0){
                    matrix[i][j] = 0;
                }
            }
        }
        if(rowZero){
            for (int i = 0; i < n; i++) {
                matrix[0][i] = 0;
            }
        }
        if(colZero){
            for (int i = 0;i < m;i++){
                matrix[i][0] = 0;
            }
        }
        return matrix;
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45

四、测试

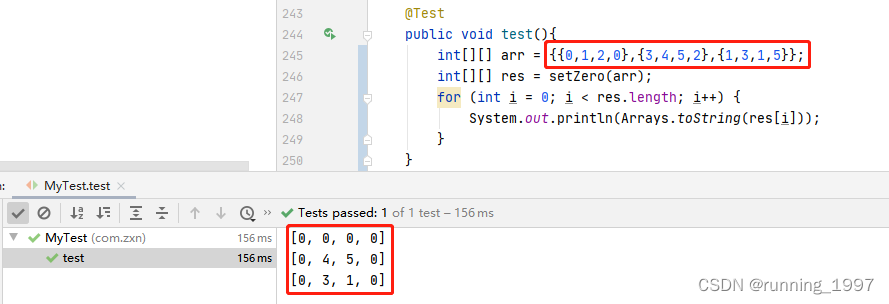
五、结束