堆、堆排序、堆应用

一、概述

“堆”（Heap），原地排序、时间复杂度O(nlogn)的排序算法。

• 堆是一个完全二叉树；
• 堆中每一个节点的值都必须大于等于（或者小于等于）其子树中每个节点的值；

二、如何实现一个堆

使用数组来存储
数组中下标为 i 的节点的左子节点，就是下标为 i∗2 的节点，右子节点就是下标为 i∗2+1 的节点，父节点就是下标为 2i​ 的节点。

往堆中插入一个数据（堆化）

• 从下往上堆化
  

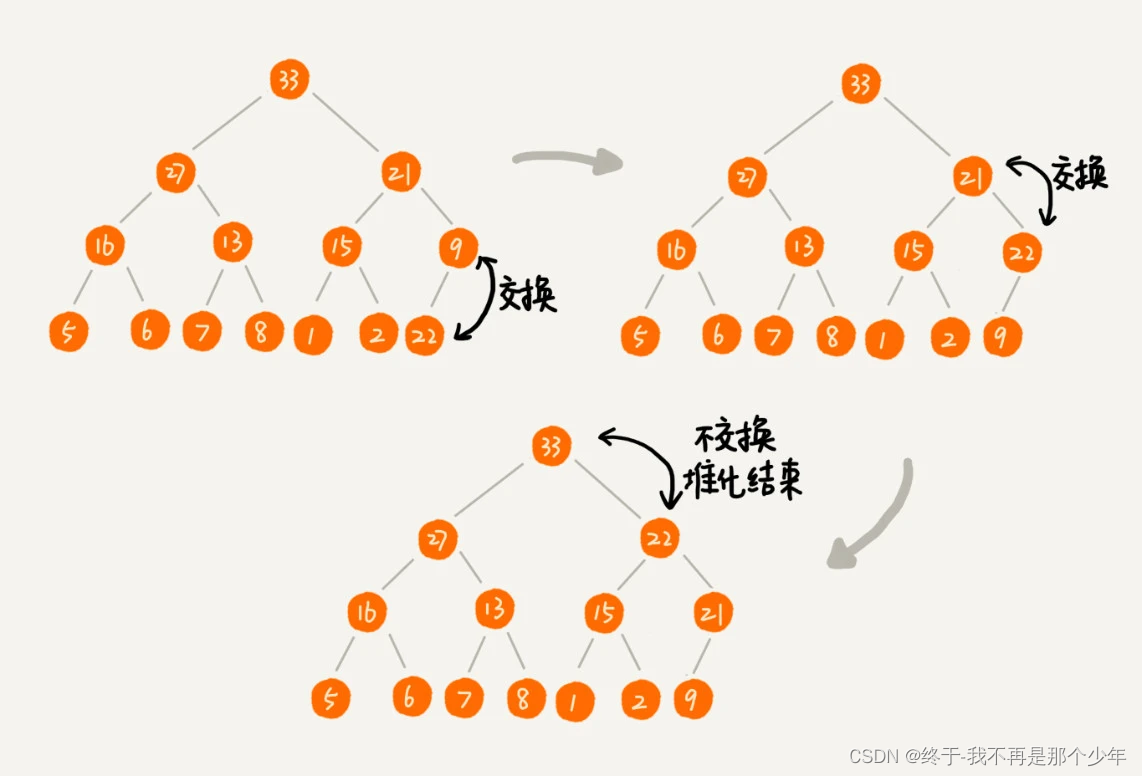
• 从上往下堆化

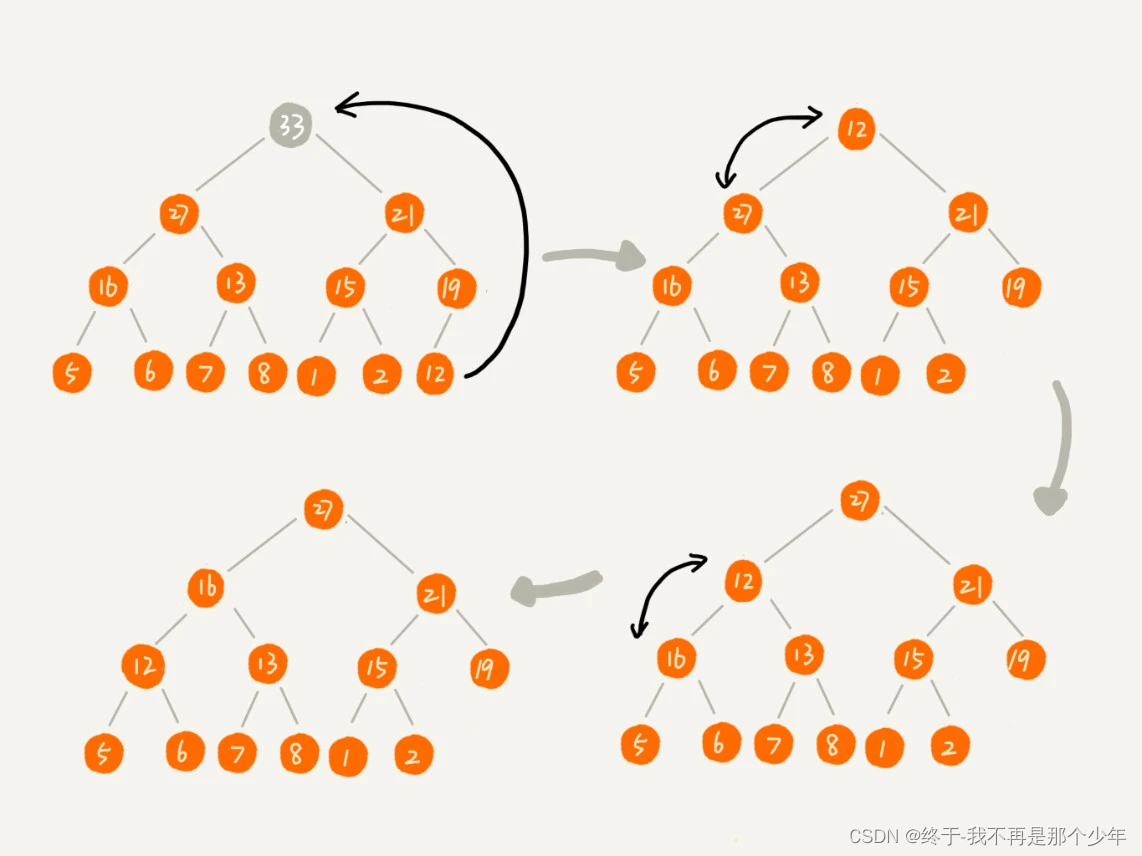
删除堆顶元素
可以选择删除堆顶元素后，将堆中的最后一个元素放到堆顶，然后进行从上往下堆化。包含n个节点的完全二叉树，树的高度不会查过log2​n，所以堆化的时间复杂度和树的高度成正比，也就是O(logn)。

三、如何基于堆实现排序

1、建堆

1. 起始堆中只有一个元素，下标为1的数据，然后根据前面的插入操作，将2到下标n的数据依次插入到堆中；
2. 从后往前处理数据，叶子节点往下堆化只能自己跟自己比较，所以从最后一个非叶子节点开始，依次堆化；
   
   

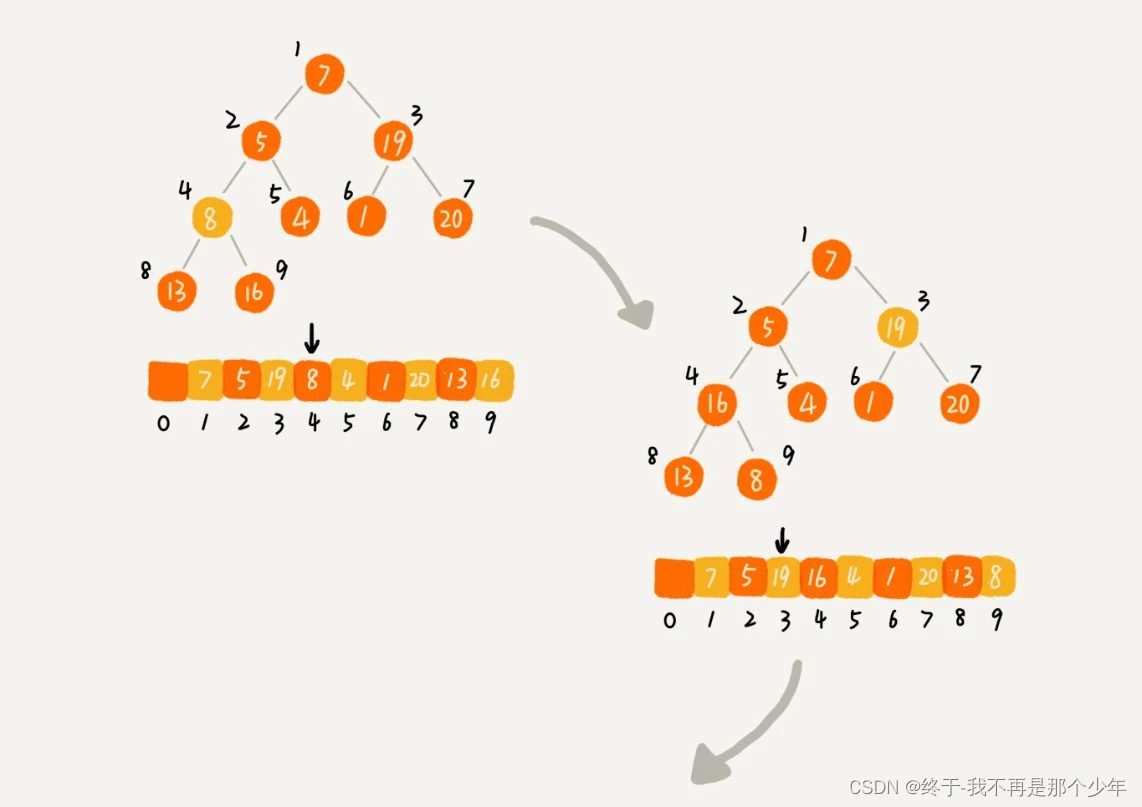
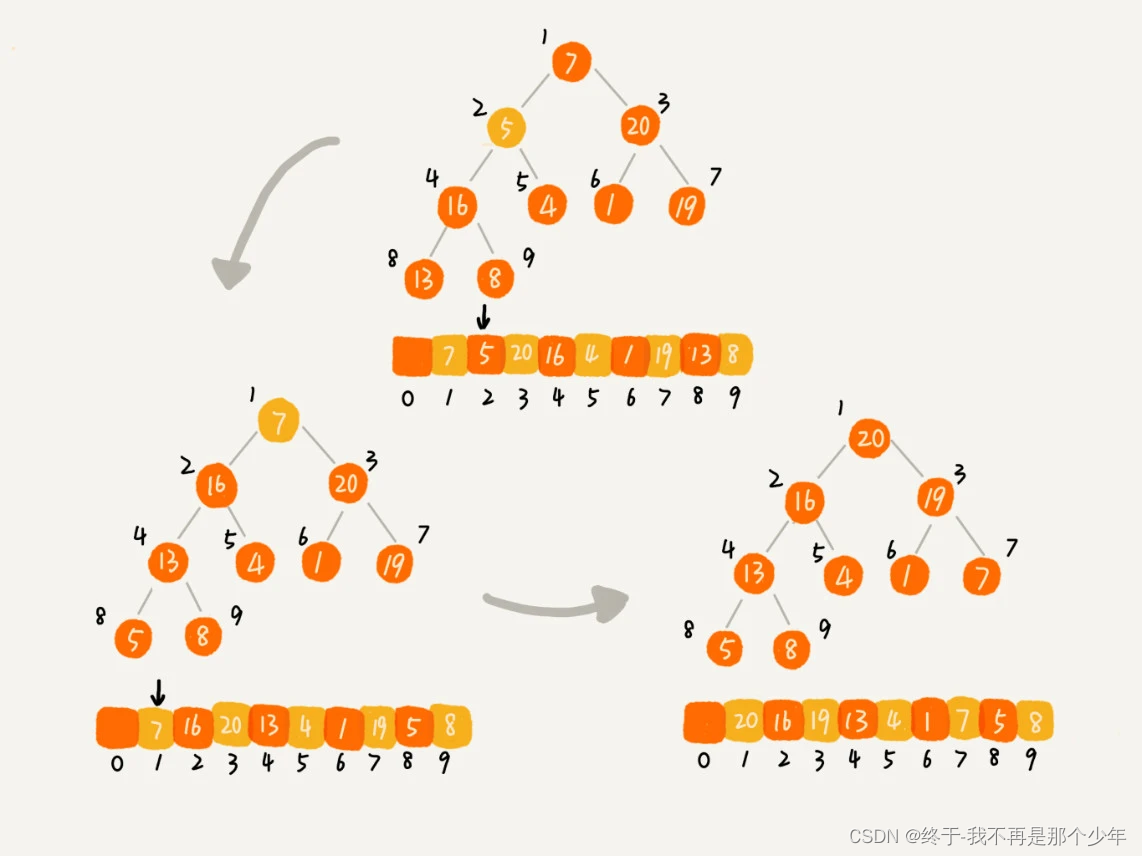
private static void buildHeap(int[] a, int n) {
  for (int i = n/2; i >= 1; --i) {
    heapify(a, n, i);
  }
}

private static void heapify(int[] a, int n, int i) {
  while (true) {
    int maxPos = i;
    if (i*2 <= n && a[i] < a[i*2]) maxPos = i*2;
    if (i*2+1 <= n && a[maxPos] < a[i*2+1]) maxPos = i*2+1;
    if (maxPos == i) break;
    swap(a, i, maxPos);
    i = maxPos;
  }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

那么建堆时间复杂度是多少？
O(n)。

2、排序
堆化为大顶堆后，数据已经按照顺序存放了，所以将堆顶数据取出，然后将最后一个元素放入堆顶进行堆化，依次进行。

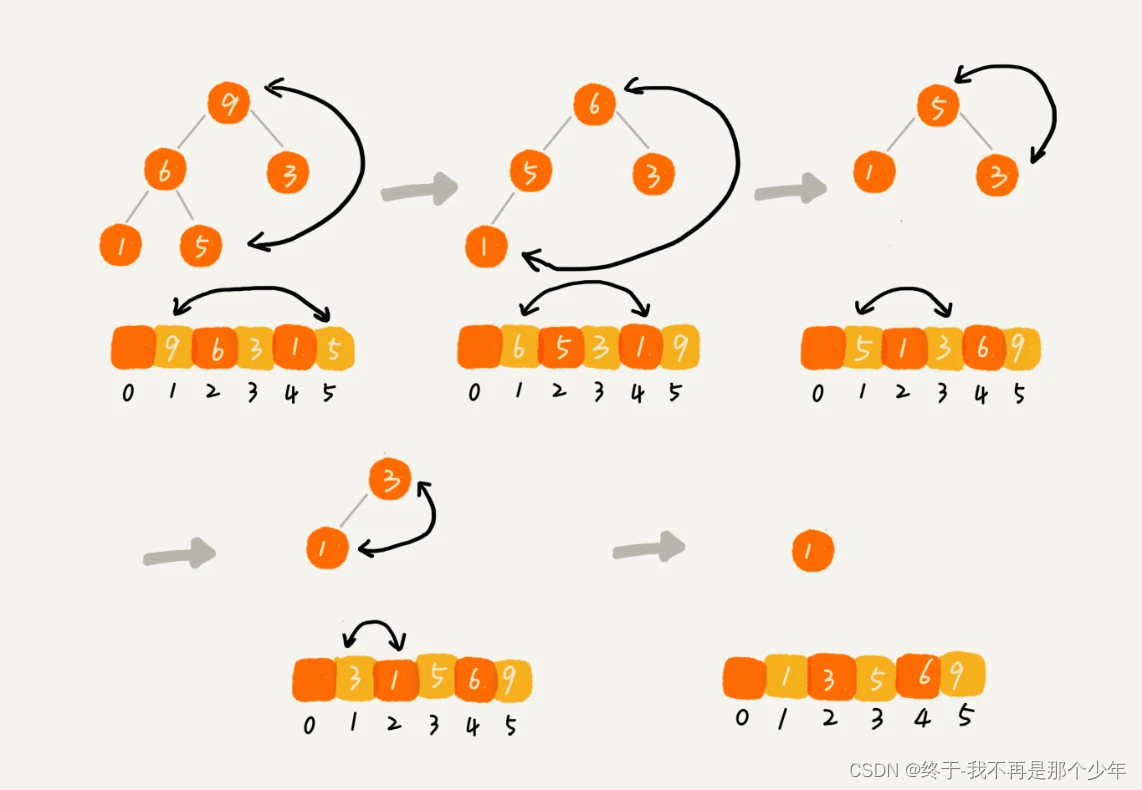
// n表示数据的个数，数组a中的数据从下标1到n的位置。
public static void sort(int[] a, int n) {
  buildHeap(a, n);
  int k = n;
  while (k > 1) {
    swap(a, 1, k);
    --k;
    heapify(a, k, 1);
  }
}
1
2
3
4
5
6
7
8
9
10

时间复杂度：建堆O(n)，排序O(nlogn)，因此整体时间复杂度是O(nlogn)。

四、堆排序和快速排序对比

• 快速排序，数据是顺序访问。而对于堆排序，数据跳着访问，这样对于CPU缓存不友好。
• 同样的数据，排序中，堆排序的数据交换次数多于快速排序。

五、堆排序的应用

1、优先级队列

• 合并有序小文件：100个小文件，每个文件大小100MB，每个文件里都是有序的字符串，希望将这100个文件合并成一个有序的大文件。操作类似于归并排序，从100个文件中，各取一个字符串，放入数组中，然后比较大小，再把最小的字符串放入合并后的大文件，并从数组中删除。另外可以组建小顶堆，每次取堆顶元素放入合并的大文件，在从小文件中取下一个字符串放入堆中，依次玄幻操作。
• 高性能服务器：定时器中维护很多定时任务，每个任务都有一个出发执行的时间点，定时器需要固定时间（1S），扫描一遍任务列表，查看是否有任务到达执行时间。如果把任务列表按照还需要等待时间的长短设计为一个小顶堆，那么定时器只需要到点0去看看堆顶的任务有没有到达执行时间就可，然后计算新的堆顶任务剩余的时间T，然后等待T秒再来取任务。

2、利用堆求Top K
针对静态数据集合，组件一个大小为K的大顶堆，依次从数组中取元素和堆顶元素进行比较，遍历完数组后，堆中的元素就是Top k数据了。遍历数组时间复杂度时O(n)，每次堆化需要O(logK)的时间复杂度，所以整体最坏情况下，n个元素都入堆依次，总的时间复杂度就是O(nlogK)。

3、利用堆求中位数
对于静态数据，中位数是固定的，可以先排序，第n/2个数据就是中位数。每次询问中位数时可以直接返回，当时如果是动态数据集合时，中位数不停的变动，每次询问都需要排序。
可以借助堆，维护一个大顶堆存前n/2或n/2+1个数据，再维护一个小顶堆，存后n/2个数据。新加入一个数据时，如果数据小于大顶堆中的元素，将数据插入大顶堆；否则，将数据插入到小顶堆。如果插入后两个堆中的数据不满足前面的约定，从一个堆中取出元素移动到另一个堆中。

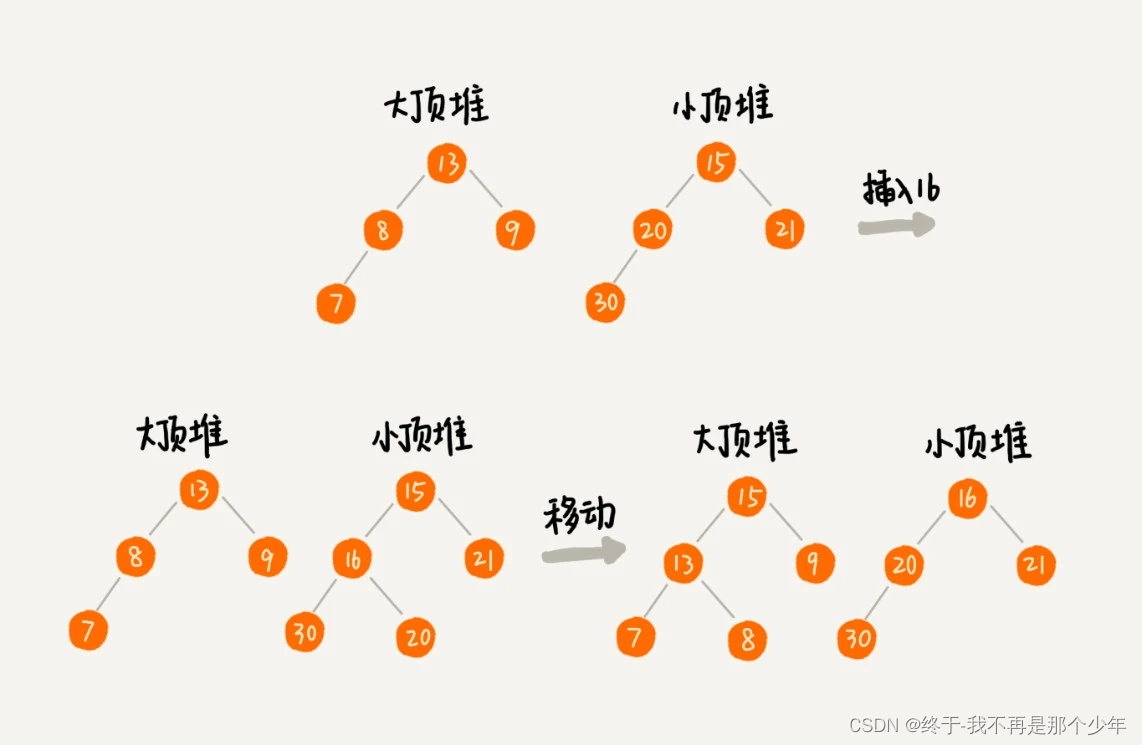
如何求接口的99%相应时间？
将上面的大小堆个数比按照99:1设计。

4、如何获取Top 10最热门的搜索关键词
假设现在有一个包含 10 亿个搜索关键词的日志文件，如何能快速获取到热门榜 Top 10 的搜索关键词呢？
单机环境，内存1GB。
首先统计每个关键词出现的频率，使用散列表、平衡二叉树或者其他支持快速查找、插入的数据结构记录关键词及其出现的次数。
顺序扫描10亿个关键词，扫描到后在散列表中查找，有的话次数+1，没有的话插入，以此类推。然后构建Top K的小顶堆，遍历散列表，依次与堆顶元素进行对比。遍历完散列表后，堆中的元素就是Top K频率的关键词。
如果10亿中的关键词很多，假如说有1亿条，每个关键词平均长度50字节，那么存储就需要5GB的内存空间，那么散列表为了避免频繁冲突。所以需要的内存空间大。1GB可能不够用。因此所以需要创建10个空文件00、01、02…，09，遍历10亿个关键字，按照哈希算法将结果取10的模，得到结果就是此关键词被分到的文件编号。然后利用散列表和堆，分别求出每个文件的Top 10，然后将每个文件的Top 10放在一块100个关键词求其Top 10就可。

5、求每间隔1小时新闻网站点击Top 10的新闻
有一个访问量非常大的新闻网站，希望将点击量排名 Top 10 的新闻摘要，滚动显示在网站首页 banner 上，并且每隔 1 小时更新一次。如何来实现呢？
根据新闻个数构建散列表，每点击一次更新其点击量；
每隔一个小时遍历散列表维护一个大小为10的小顶堆；