第十二章 哈希表与字符串哈希

一、哈希表

1、什么是哈希表

在之前的文章中，我们学习过离散化的算法，但是我们之前学过的离散化算法需要先去排序，所以效率较低。但是今天我们所学的哈希表同样是为了解决离散化的问题，但是其时间复杂度只有O(1)。依旧是空间换时间。

2、算法逻辑

（1）哈希函数

我们假设存在一个哈希函数（hash）。这个函数的作用就是将一个大范围的数字映射到一个小范围的数字中。这个哈希函数仅仅是听起来很高尚，其实就是取模运算。我们将一系列的数字和100取模，那么最终得到的映射值就都属于0到99的。所以哈希函数就是取模。但是这里有一个问题，101%100=1,1001%100=1。这两个数字映射到了同一个映射值，发生了冲突。那么我们如何解决这个冲突呢？

（2）冲突解决

如上图所示，我们创建一个数组，这个数组存储不同的映射值，然后每个映射值都连接了一个链表，这个链表存储的都是具有相同映射值的值，例子如图中所示。这样的话，我们可以先去寻找映射后的值，找到对应的链表，再去遍历链表，得到对应的原值。

3、算法模板

#include
#include
using namespace std;
const int N=1e5+3;
int h[N],e[N],ne[N],idx;

void insert(int x)
{
    int p=(x%N+N)%N;
    e[idx]=x;
    ne[idx]=h[p];
    h[p]=idx++;
}

bool quary(int x)
{
    int p=(x%N+N)%N;
    for(int i=h[p];i!=-1;i=ne[i])
    {
        if(e[i]==x)
        {
            return true;
        }
    }
    return false;
    
}

int main()
{
    memset(h,-1,sizeof(h));
    int n;
    cin>>n;
    while(n--)
    {
        string op;int x;
        cin>>op>>x;
        if(op=="I")
        {
            insert(x);
        }
        else
        {
            if(quary(x))puts("Yes");
            else puts("No");
        }
    }
    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49

二、字符串哈希

1、算法逻辑

转化成数字后，该数字可能过大，因此我们需要再对这些数字进行取模离散化。

我们通过转化，将不同的字符串转化成了一串数字，但是必定存在一种情况，即两个字符串不同，但是最终得到的结果是相同的，即发生了冲突。那么为了解决这个问题，众多人总结出了一种经验，当p取131,m取2⁶⁴ 的时候，百分之99的概率不会重复。

2、算法用途

当我们知道各种前缀对应的数字后，我们可以迅速得到任意一段的子串对应的数字，即迅速得到一截子串。

想要得到BC这段子串，我们可以让AB段和BC段通过某种运算得到。
那么如何运算呢?

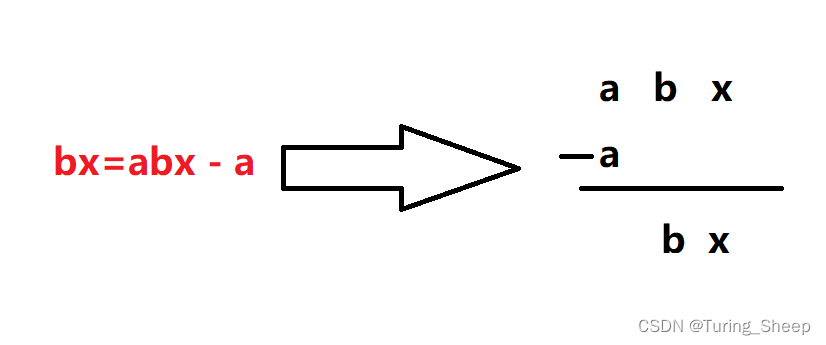
示意图如下图所示，但实际上a并不是和a对齐的，而是a和x对齐的。

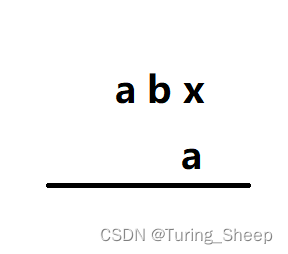
此时就发生了错误，因此我们再计算子串的时候，要做的第一件事就是位数对齐。

3、算法模板

#include
using namespace std;
const int N=1e5+10;
typedef unsigned long long ull;
ull h[N],p[N];
char str[N];

ull get_hash(int l,int r)
{
    return h[r]-h[l-1]*p[r-l+1];//位数对齐
}

int main()
{
    int n,m,px=131;
    p[0]=1;
    scanf("%d%d%s",&n,&m,str+1);
    for(int i=1;i<=n;i++)
    {
        p[i]=p[i-1]*px;
        h[i]=h[i-1]*px+str[i];//利用了前缀和的思路
    }
    while(m--)
    {
        int l1,r1,l2,r2;
        scanf("%d %d %d %d",&l1,&r1,&l2,&r2);
        if(get_hash(l1,r1)==get_hash(l2,r2))puts("Yes");
        else puts("No");
    }
    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

我们这里利用unsigned long long去存储的话，我们会发现，当数据溢出的时候会发生数据截断。此时，就相当于取模了。