E-梅莉的市场经济学

E-梅莉的市场经济学

题目背景

梅莉这个学期选修了经济学。但是主修心理学的她实在不擅长经济领域的分析，为此她时常抱怨自己学不会，想退课。

但是如果现在退掉的话这学期的学分就不够啦，因此她根据“梦中”的经历，“胡诌”了一个简单到不现实的市场模型，并依据这个模型编起了 essay。为了方便地编出图表，她需要写一个程序来查询每个时刻的市场贸易差。

题目描述

市场每一天的贸易差可以视为一个有周期性规律的数列 $a$：$[0],[0,1,0,-1,0],[0,1,2,1,0,-1,-2,-1,0],[0,1,2,3,2,1,0,-1,-2,-3,-2,-1,0]\dots$ 具体而言，$a$ 可以被分为无穷段，第 $i$ 段的内容为 { 0 , 1 , ⋯   , i , i − 1 , ⋯   , 0 , − 1 , ⋯   , − i , − i + 1 , ⋯ 0 } \{0,\allowbreak 1,\allowbreak \cdots,\allowbreak i,\allowbreak i-1,\allowbreak \cdots,0,\allowbreak -1,\allowbreak \cdots,\allowbreak -i,\allowbreak -i+1,\allowbreak \cdots 0\} {0,1,⋯,i,i−1,⋯,0,−1,⋯,−i,−i+1,⋯0}。如下图所示，是将 $a$ 数列内的前一些点绘制在坐标轴上的情况：

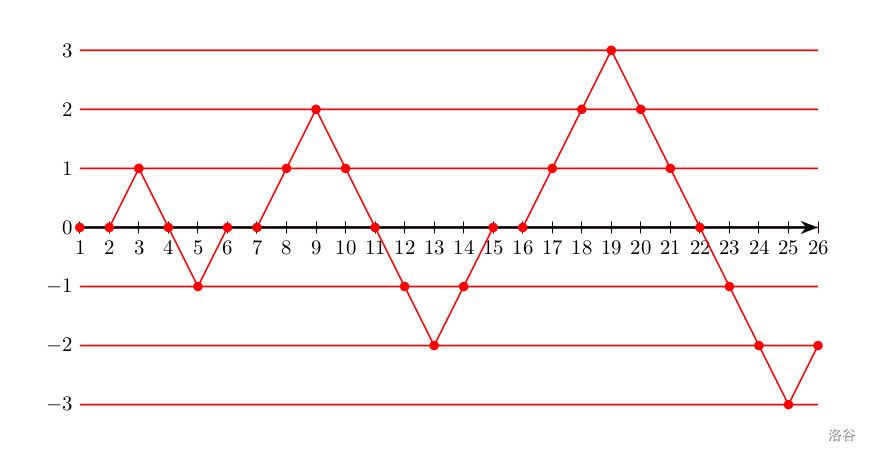
现在梅莉对市场发起了 $q$ 次询问，每次她会给定一个 $k$，希望求出 $a_k$ 是多少。

输入格式

• 第一行有一个正整数 $q$，表示询问次数。
• 接下来 $q$ 行，每行一个正整数 $k$，描述每次询问。

输出格式

• 输出共 $q$ 行。对于每次询问，输出对应的结果。

样例 #1

样例输入 #1

9
1
10
100
1000
10000
100000
1000000
10000000
100000000
1
2
3
4
5
6
7
8
9
10

样例输出 #1

0
1
6
-9
-11
-128
406
1629
5154
1
2
3
4
5
6
7
8
9

提示

对于所有数据，$1\le q\le 10^5$，$1\le k\le 4\times 10^{18}$。

题解

#include
using namespace std;
#define ll long long 
const int N = 1e5 + 10;
const ll MK = 4e18;
int n;

ll inline getSum(ll x) {
	return x * (x * 2 - 1);
}

ll getIndex(ll k) {
	ll l = 0, r = 3e9;
	ll mid, vl, vr;
	while (l < r)
	{
		mid = (l + r) >> 1;
		vl = getSum(mid - 1);
		vr = getSum(mid);
		if(vl < k && vr >= k) { 
			return mid;
		} else if( vl >= k) {
			r = mid;
		} else if( vr < k) {
			l = mid + 1;
		}
	}
	return l;
}

int main() {

	cin >> n;
	ll k, res = 0;
	while(n--) {
		cin >> k;
		ll index = getIndex(k);
		k -= getSum(index - 1);
		if(k <= index) {
			res = k - 1;
		} else if(k <= 3 * index - 2) {
			k -= index;
			res = (index - 1) - k;
		} else {
			k -= 3 * index - 2;
			res = -(index - 1) + k; 
		}
		cout << res << endl;
	}

	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52