内点法最优潮流matlab程序

内点法最优潮流matlab程序
一、概述最优潮流问题
1.最优潮流和基本潮流的比较潮流计算可以归结为针对一定的扰动变量p(负荷情况)，根据给定的控制变量u(如发电机的有功出力、无功出力或节点电压模值等)，求出相应的状态变量x(如节点电压模值及角度)，这样通过一次潮流计算得到的潮流解决定了电力系统的一个运行状态。这种潮流计算也可以称之为基本潮流(或常规潮流)计算，一次基本潮流计算的结果主要满足了潮流方程式或变量间等式约束条件

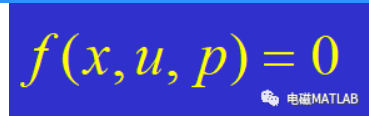
一次潮流计算所决定的运行状态可能由于某些状态变量或者作为u,x 函数的其它变量在数值上超出了它们所容许的运行限值(即不满足不等式约束条件)，因而在技术上并不是可行的。工程实际上常用的方法是调整某些控制变量的给定值，重新进行前述的基本潮流计算，这样反复进行，直到所有的约束条件都能够得到满足为止。这样便得到了一个技术上可行的潮流解。

由于系统的状态变量及有关函数变量的上下限值间有一定的间距，控制变量也可以在其一定的容许范围内调节，因而对某一种负荷情况，理论上可以同时存在为数众多的、技术上都能满足要求的可行潮流解。每一个可行潮流解对应于系统的某一个特定的运行方式，具有相应总体的经济上或技术上的性能指标(如系统总的燃料消耗量、系统总的网损等)，为了优化系统的运行，就有需要从所有的可行潮流解中挑选出上述性能指标为最佳的一个方案。而这就是本节要讨论的最优潮流所要解决的问题。

因此所谓最优潮流，就是当系统的结构参数及负荷情况给定时，通过控制变量的优选，所找到的能满足所有指定的约束条件，并使系统的某一个性能指标或目标函数达到最优时的潮流分布。

综上所述，最优潮流和基本潮流比较，有以下不同点：
(1)基本潮流计算时控制变量u是事先给定的；而最优潮流中的u则是可变而待优选的变量，为此在最优潮流模型中必然有一个作为u优选准则的目标函数。
(2)最优潮流计算除了满足潮流方程这一等式约束条件之外，还必须满足与运行限制有关的大量不等式约束条件。
(3)进行基本潮流计算是求解非线性代数方程组；而最优潮流计算由于其模型从数学上讲是一个非线性规划问题，因此需要采用最优化方法来求解。
(4)基本潮流计算所完成的仅仅是一种计算功能，即从给定的u求出相应的x；而最优潮流计算则能够根据特定目标函数并在满足相应约束条件的情况下，自动优选控制变量，这便具有指导系统进行优化调整的决策功能。

二、最优潮流计算的内点法
内点法则是一种在可行域内部寻优的方法。1984年，Karmarkar提出的内点法具有多项式计算复杂性，在求解大规模线性规划问题时，计算速度比单纯形法快50倍以上。 1986年，Gill将内点法推广到非线性规划领域。
1）基本思想
内点法最初的基本思想是希望寻优迭代过程始终在可行域内进行，因此，初始点应取在可行域内，并在可行域的边界设置“障碍”使迭代点均为可行域的内点。
2）存在的困难
但对实际大规模系统，初始可行点的寻找比较困难。
3）改进方法－跟踪中心轨迹内点法
跟踪中心轨迹内点法对此作了改进，只要求在寻优过程中松弛变量和拉格朗日乘子满足简单的大于零或小于零的条件，可代替原来必须在可行域求解的要求，使计算过程大为简化。
4）跟踪中心轨迹内点法详介
最优潮流的非线性优化模型：

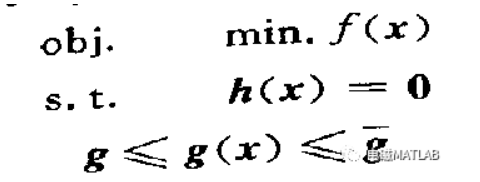
首先，通过添加松弛变量，将不等式约束化为等式约束：


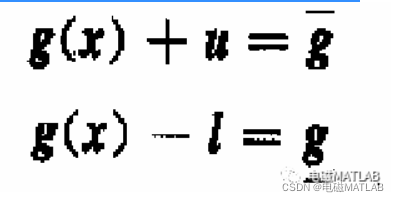
然后，把目标函数改造为障碍函数，该函数在可行域内应近似于原目标函数f（x），而在边界时变得很大，因此可得优化问题B:



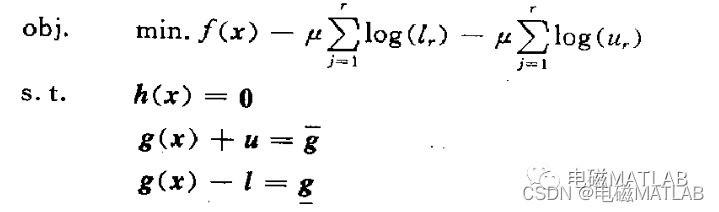
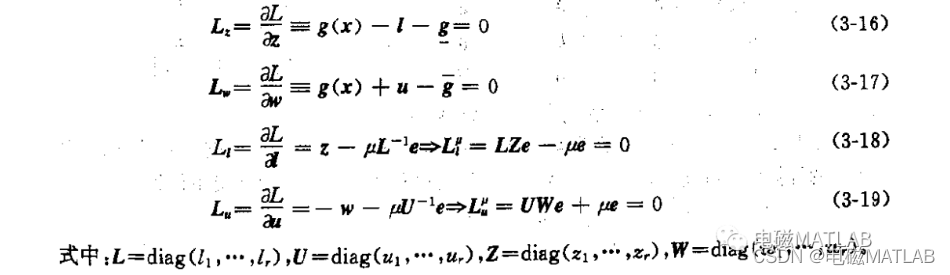
最后，对式（3－14）（3－19）组成的非线性方程组，用牛顿－拉夫逊法求解。具体从略，（详见王锡凡主编《现代电力系统分析》）

三、算例
1）王锡凡主编《现代电力系统分析》算例3-1系统解构及参数如下图

2）程序运行结果
电压结果

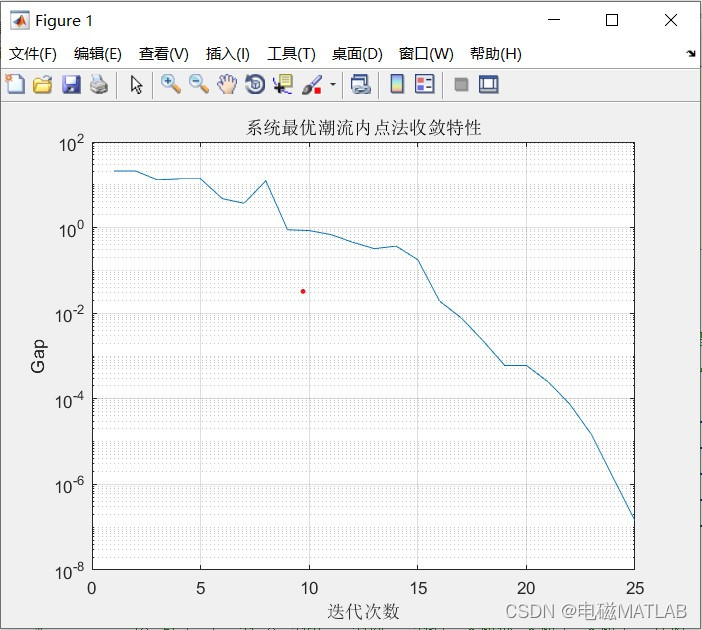
电源出力

节点电压

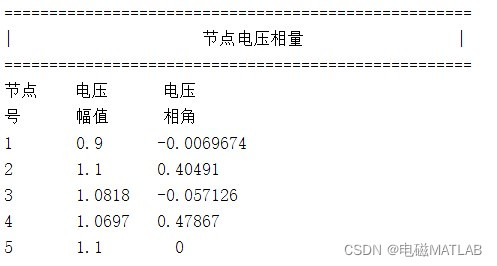
支路功率

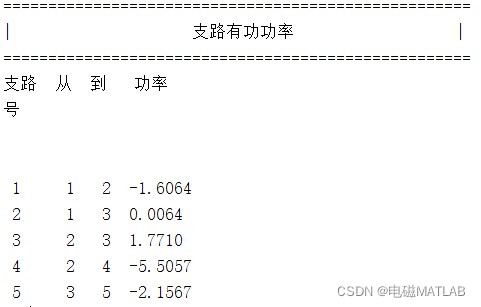
四、matlab程序

% 最优潮流（OPF）的内点法求解
% 说明：本程序包括一个主文件main.m和三个函数文件makeY.m，Coeff.m和dPQ.m，四个文件均应放在MATLAB当前目录下
% 运行main.m，会将计算结果打印到屏幕并保存至文件solution.txt中
clc;
clear;
close all
tic;
%% 算例数据
%节点数据表
%       1  2  3   4        5       6        7        8       9      10      11     12      13      14     15      16    17    18    19
%     节点 区 类 电压     相角    有功     无功     有功    无功   电压   期望    乏值    乏值    并联   并联   远端控 节点  电压  电压
%      号  号 型                  负荷     负荷     出力    出力   基准   电压    上限    下限    电导   电纳  制节点号 号   上限  下限
%
  N=[  1  1  0 1.0000   0.00     1.60     0.80     0.00    0.00  230.00 1.032   0.0000  0.0000  0.0000  0.0000    0    1    1.1   0.9
        2  1  0 1.0000   0.00     2.00     1.00     0.00    0.00   18.00 1.025   0.0000  0.0000  0.0000  0.0000    0    2     1.1   0.9
        3  1  0 1.0000   0.00     3.70     1.30     0.00    0.00   13.80 1.025   0.0000  0.0000  0.0000  0.0000    0    3    1.1   0.9
        4  1  2 1.0000   0.00     0.00     0.00     4.50    0.00  230.00 1.026   0.0000  0.0000  0.0000  0.0000    0    4     1.1   0.9
        5  1  3 1.0500   0.00     0.00     0.00     4.50    1.45    0.00 0.996   0.0000  0.0000  0.0000  0.0000    0    5     1.1   0.9];

%支路数据表
%          1  2  3  4  5  6   7      8       9     10    11     12     13    14    15       16     17   18   19   20   21   22    
%          从 到 区 区 电 类 电阻   电抗   电纳  支路额 支路下 支路上  控制  位 变压器最 移相器最 最小 最大 步长 最小 最大 支路  
%                号 号 路 型                     定功率 限功率 限功率 母线号 置 终传输比 终移相角 变比 变比      电压 电压  号
  B=[     1  2  1  1  1  0  0.040  0.2500 0.50      0.    0.    2.      0    0    1.0       0.0    0.0  0.0  0.0  0.0 0.0    1
           1  3  1  1  1  0  0.100  0.3500   0.0      0.    0.    0.65    0    0    1.0       0.0    0.0  0.0  0.0  0.0 0.0    2
           2  3  1  1  1  0  0.080  0.3000 0.50      0.    0.    2.      0    0    1.0       0.0    0.0  0.0  0.0  0.0 0.0    3
           2  4  1  1  1  1  0.0    0.0150   0.0      0.    0.    6.      0    0    1.050     0.0    0.0  0.0  0.0  0.0 0.0    4
           3  5  1  1  1  1  0.0    0.0300   0.0      0.    0.    5.      0    0    1.050     0.0    0.0  0.0  0.0  0.0 0.0    5];
    
%发电机数据表
%             1    2     3    4    5   6       7         8         9   
%            发电 节点 有功 无功 有功 无功   二次      一次       常数  
%            机号  号  上界 上界 下界 下界   系数      系数        项
  Gen=[     1    4    8.0  3.0  1.0  -3.0  50.4395  200.4335  1200.6485
            2     5    8.0  5.0  1.0  -2.1  200.55   500.746   1857.201];

[num_node,~] = size(N);
[num_branch,~] = size(B);
% 不同类型节点个数
num_PQ = 0;
num_PV = 0;
for k = 1:num_node
  if (N(k,3) == 0)
      num_PQ = num_PQ+1;
  end
    if (N(k,3) == 2)
      num_PV = num_PV+1;
    end
end
。。。。。。。。。略
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50