牛顿法（牛顿拉夫逊）配电网潮流计算matlab程序

牛顿法配电网潮流计算matlab程序
传统牛顿—拉夫逊算法，简称牛顿法，是将潮流计算方程组F(X)=0，进行泰勒展开。因泰勒展开有许多高阶项，而高阶项级数部分对计算结果影响很小，当忽略一阶以上部分时，可以简化对方程的求解计算。当忽略一阶以上部分后，牛顿法的求解过程实质是逐次线性化，这是反复形成、求解修正方程的过程[16]。其方程式如下：

（18）
在公式（18）中，和分别表示状态变量与其修正量组成的列向量；为方阵，一般叫作雅可比矩阵，第i行j列元素为 ，它的大小为第i个函数对第j个变量求偏导；k则表示阵元素都在处取；同时，F(X)是由n个函数组成的n维列向量；在极坐标下，节点电压可如下表示：

（19）
若和为已知大小的功率，与从节点电压求得的有功和无功功率之差，为功率的不平衡量，则节点功率不平衡量可用如下公式计算：

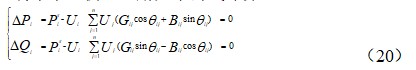
（20）
节点功率可用各节点电压模值与相位表示，如下公式所示：

（21）
式（21）中，为节点i和j的相位差。
由以公式（18）-（21）推得牛顿法下，其潮流计算方程可写为：

（22）
公式（22）中，雅可比矩阵的各元素为

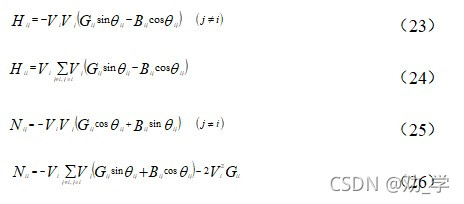
（23）
（24）
（25）
（26）

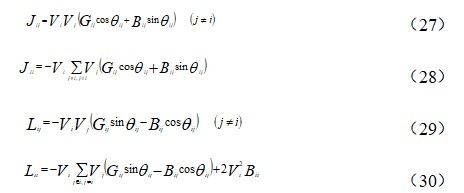
（27）
（28）
（29）
（30）
其中，节点导纳矩阵的元素由Gij 、Bij表示。
随着国内外配电系统自动化水平不断提高，电力行业人员也开始更加深入地研究配电网系统。配电网潮流计算作为DMS（配电管理系统）的重要基础，受到广大行业界人士的关注。因此，配电网潮流计算，已然成为配电网分析的重要内容。配电网与输电网相比，两者有明显不同，前者一般采用网格结构，线路参数R/X的值较大，三相负荷不对称程度明显。这些特点使得在输电网中计算有效，如牛顿法，不再适用于配电网。为此，有学者提出了适用于配电网的潮流算法，主要包括基于回路方程的潮流算法、前推回推法和改进的牛顿-拉夫逊法[17]（简称改进的牛拉法）。其中，基于回路方程的方法具有较强的网格处理能力和良好的收敛性，但该方法的节点数和分支数处理非常复杂。前推回推法是针对配电网的树状特性，可以避免潮流计算中的病态条件，同时速度更快。然而，由于其公式和算法与牛顿潮流算法不同，其在其它方面（如潮流优化）的应用将受到限制。
改进牛顿法通过对传统法进行一定的近似，将J阵写成UDUT 的形式。U仅由网络拓扑决定，是一个上三角矩阵；D是一个对角矩阵。在牛拉法中，需要对J阵因子分解与前代回代，改进法则只有前推回代的计算过程。它很好地改善了传统法以及前推回推法。经过算例计算结果证明，改进法可以避免J阵病态，且拥有前推回代法的收敛速度、精度，又由于它属于牛顿型算法，所以该算法已经得到了广泛的运用[18]。

下面附带电力系统分析牛顿法算例及matlab程序：
网络结构如下：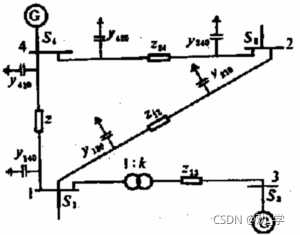
系统参数如下：
在上图所示的简单电力系统中，系统中节点1、2为PQ节点，节点3为PV节点，节点4为平衡节点，已给定P1s+jQ1s=-0.30-j0.18 P2s+jQ2s=-0.55-j0.13 P3s=0.5 V3s=1.10 V4s=1.05∠0°
容许误差ε=10-5
节点导纳矩阵：

各节点电压：
节点 e f v ζ
1.0.984637 -0.008596 0.984675 -0.500172
2.0.958690 -0.108387 0.964798 -6.450306
3.1.092415 0.128955 1.100000 6.732347
4.1.050000 0.000000 1.050000 0.000000

各节点功率：
节点 P Q
1-0.300000 -0.180000
2–0.550000 -0.130000
3 0.500000 -0.551305
4 0.367883 0.264698

matlab程序如下：

// 牛顿法潮流计算matlab程序
clc;
Y=[1.042093-8.242876i   -0.588235+2.352941i   3.666667i   -0.453858+1.891074i;
-0.588235+2.352941i     1.069005-4.727377i       0        -0.480769+2.403846i;
3.666667i                   0                   -3.333333i            0;
-0.453858+1.891074i      -0.480769+2.403846i       0        0.934627-4.261590i];
%导纳矩阵
e=[1  1  1.1  1.05];%初始电压
f=zeros(4,1);
V=zeros(4,1);%节点电压
Ws=[-0.3 ; -0.18 ; -0.55 ; -0.13 ; 0.5 ; 1.1];%初始功率
W=zeros(6,1);
n=length(Y);%节点数
J=zeros(2*(n-1));%雅可比矩阵
delta_v=zeros(1,6);
delta_w=Ws;
G=real(Y);
B=imag(Y);
S=zeros(4,2);
c=0;%循环次数
m=input('请输入PQ节点数：');
 while max(abs(delta_w))>10^-5
for i=1:(n-1)%以下为求取雅可比矩阵
    for j=1:(n-1)
       if (i~=j)
           J(2*i-1,2*j-1)=-(G(i,j)*e(i)+B(i,j)*f(i));
           J(2*i,2*j)=-J(2*i-1,2*j-1);
           J(2*i-1,2*j)=B(i,j)*e(i)-G(i,j)*f(i);
           J(2*i,2*j-1)=J(2*i-1,2*j);
       end        
    end    
end
for j=1:(n-2)  
      J(6,2*j-1)=0;
      J(6,2*j)=0;   
end%以上为非对角线元素
s1=0;
s2=0;
for i=1:(n-1) 
    for j=1:n
   s1=s1+(G(i,j).*e(j)-B(i,j).*f(j));
   s2=s2+(G(i,j).*f(j)+B(i,j).*e(j));
    end
    J(2*i-1,2*i-1)=-s1-G(i,i) *e(i)-B(i,i)*f(i);
    J(2*i-1,2*i)=-s2+B(i,i) *e(i)-G(i,i)*f(i);
    s1=0;
    s2=0;
end
for i=1:m
    for j=1:n
   s1=s1+G(i,j).*f(j)+B(i,j).*e(j);
   s2=s2+(G(i,j).*e(j)-B(i,j).*f(j));
    end
     J(2*i,2*i-1)=s1+B(i,i) *e(i)-G(i,i)*f(i);
    J(2*i,2*i)=-s2+G(i,i) *e(i)+B(i,i)*f(i);
    s1=0;
    s2=0;
end
J(6,5)=-2*e(3);
J(6,6)=-2*f(3);%对角线元素求解
for i=1:m
    for j=1:n
   s1=s1+e(i)*(G(i,j).*e(j)-B(i,j).*f(j))+f(i)*(G(i,j).*f(j)+B(i,j).*e(j));
   s2=s2+f(i)*(G(i,j).*e(j)-B(i,j).*f(j))-e(i)*(G(i,j).*f(j)+B(i,j).*e(j));   
    end   
      delta_w(2*i-1)=Ws(2*i-1)-s1;
      delta_w(2*i)=Ws(2*i)-s2;   
      W(2*i-1)=s1;
      W(2*i)=s2;
      s1=0;
      s2=0;
end
for j=1:n
    s1=s1+e(3)*(G(3,j).*e(j)-B(3,j).*f(j))+f(3)*(G(3,j).*f(j)+B(3,j).*e(j));
end
delta_w(5)=Ws(5)-s1;
delta_w(6)=(Ws(6)^2-(e(3)^2+f(3)^2));
W(5)=s1;
W(6)=sqrt(e(3)^2+f(3)^2);%以上求功率差值
delta_v=-inv(J)*delta_w;
for i=1:(n-1)
   e(i)=e(i)+delta_v(2*i-1);
   f(i)=f(i)+delta_v(2*i);
end%求电压差值
c=c+1;
 end
 for x=1:4
     V(x)=e(x)+f(x)*1i;     
 end%节点电压
 s1=0;
 for x=3:4
    for j=1:4
       s1=s1+conj(Y(x,j))*conj(V(j));
    end
   S(x,1)=real(V(x)*s1);
   S(x,2)=imag(V(x)*s1);
   s1=0;
 end%PV与平衡节点功率
 for x=1:2
     S(x,1)=W(2*x-1);
     S(x,2)=W(2*x);
 end%节点功率
c  
J
V
S
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106

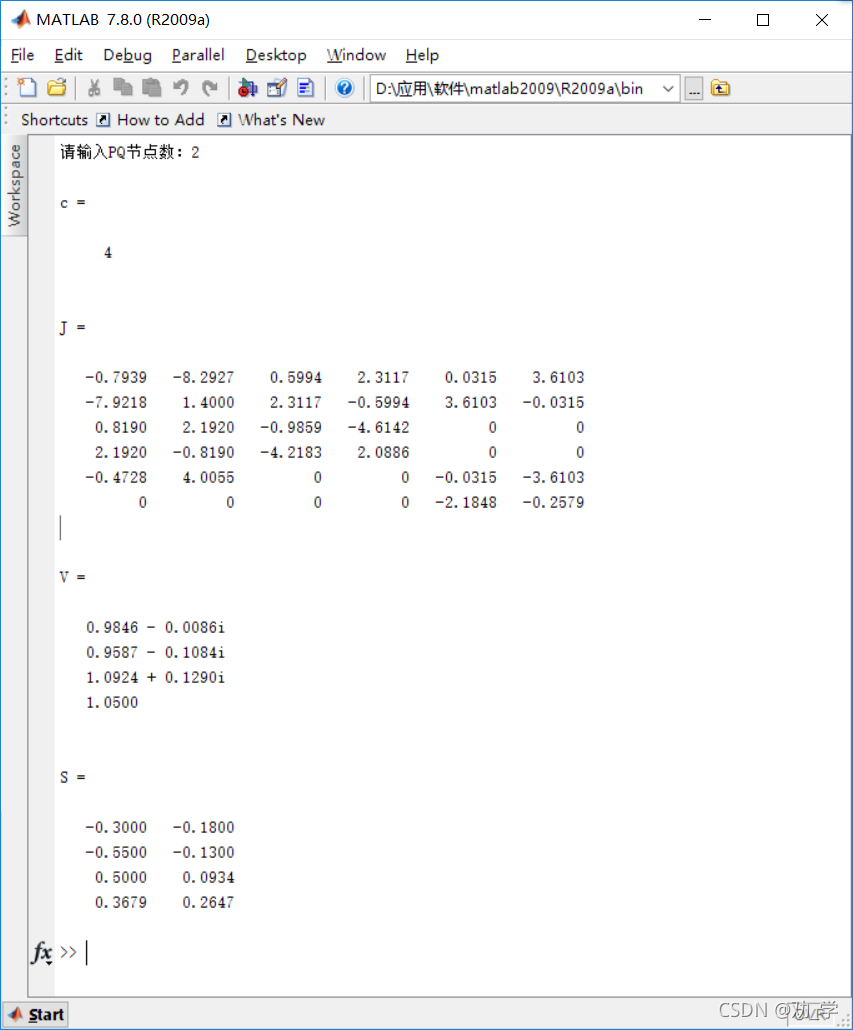
运行结果如下：