-
【ML特征工程】第 7 章 :通过K-Means 模型堆叠进行非线性特征化
🔎大家好,我是Sonhhxg_柒,希望你看完之后,能对你有所帮助,不足请指正!共同学习交流🔎
📝个人主页-Sonhhxg_柒的博客_CSDN博客 📃
🎁欢迎各位→点赞👍 + 收藏⭐️ + 留言📝
📣系列专栏 - 机器学习【ML】 自然语言处理【NLP】 深度学习【DL】

🖍foreword
✔说明⇢本人讲解主要包括Python、机器学习(ML)、深度学习(DL)、自然语言处理(NLP)等内容。
如果你对这个系列感兴趣的话,可以关注订阅哟👋
文章目录
当数据像扁平煎饼一样位于线性子空间时,PCA 非常有用。但是,如果数据形成更复杂的形状怎么办?1一个平面(线性子空间)可以被推广到流形(非线性子空间),可以将其视为以各种方式拉伸和滚动的表面。2个
如果线性子空间是一张平面纸,那么卷起的纸就是非线性流形的一个简单示例。非正式地,这称为瑞士卷(见图 7-1)。一旦滚动,2D 平面就会占据 3D 空间。然而它本质上仍然是一个二维对象。换句话说,它具有低内在维度,这是我们在“直觉”中已经触及的概念。如果我们能以某种方式展开瑞士卷,我们就会恢复 2D 平面。这是非线性降维的目标,它假设流形比它占据的完整维度更简单,并试图展开它。
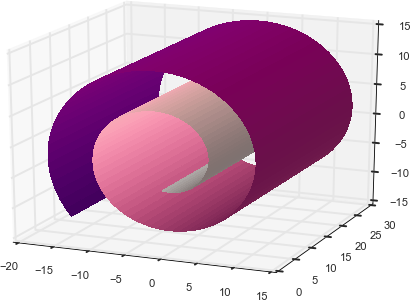
图 7-1。瑞士卷,非线性流形
关键的观察结果是,即使一个大的流形看起来很复杂,每个点周围的局部邻域通常也可以用一块平面很好地近似。换句话说,用于编码全局的补丁结构使用局部结构。3非线性降维也称为非线性嵌入或流形学习。非线性嵌入可用于将高维数据积极压缩为低维数据。它们通常用于二维或三维可视化。
然而,特征工程的目标与其说是使特征维度尽可能低,不如说是为任务找到正确的特征。在本章中,正确的特征是那些代表数据空间特征的特征。
聚类算法通常不作为局部结构学习技术呈现。但事实上,它们恰恰能够做到这一点。彼此靠近的点(其中“接近度”可以由所选指标定义)属于同一个集群。给定一个聚类,一个数据点可以用它的聚类成员向量表示。如果簇的数量小于原始特征的数量,那么新表示的维数将比原来的少;原始数据被压缩到较低的维度。我们将在本章中阐述这个想法。
与非线性嵌入技术相比,聚类可以产生更多的特征。但如果最终目标是特征工程而不是可视化,这就不是问题。
我们将使用称为k均值的通用聚类算法来说明局部结构学习的概念。它易于理解和实施。代替非线性流形减少,更贴切的说法是k - means进行非线性流形特征提取。如果使用得当,它可以成为我们特征工程库中的强大工具。
k-均值聚类
k -means 是一种聚类算法。聚类算法根据数据在空间中的布局方式对数据进行分组。它们不受监督,因为它们不需要任何类型的标签——算法的工作是仅根据数据本身的几何形状来推断集群标签。
聚类算法依赖于度量——数据点之间紧密度的度量。最流行的度量是欧氏距离或欧氏度量。它来自欧几里德几何,测量两点之间的直线距离。我们应该感觉很正常,因为这是我们在日常物理现实中看到的距离。
两者之间的欧氏距离向量x和y是x – y的ℓ 2范数。(有关ℓ 2范数的更多信息,请参阅“ℓ 2归一化”。)在数学方面,它通常写为‖x – y ‖ 2或简称‖x – y ‖。
k -means 建立一个硬聚类,这意味着每个数据点被分配到一个且仅一个集群。该算法学习定位聚类中心,使每个数据点与其聚类中心之间的欧氏距离总和最小。对于那些喜欢阅读数学而不是文字的人来说,这是目标函数:
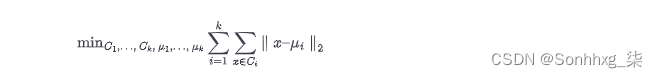
每个集群C i包含数据点的子集。簇i的中心等于簇中所有数据点的平均值:

其中n i表示簇i中的数据点数。
图 7-2显示了k均值在两个不同的、随机生成的数据集上的作用。(a) 中的数据是从具有相同方差但均值不同的随机高斯分布生成的。(c)中的数据是随机均匀生成的。这些玩具问题很容易解决,k - means 做得很好。(结果可能对簇数敏感,必须将其提供给算法。)

图 7-2。k-means 示例演示聚类算法如何划分空间
此示例的代码可在示例 7-1中找到。
示例 7-1。生成 k-means 示例的代码
- import numpy as np
- from sklearn.cluster import KMeans
- from sklearn.datasets import make_blobs
- import matplotlib.pyplot as plt
- n_data = 1000
- seed = 1
- n_clusters = 4
- # Generate random Gaussian blobs and run k-means
- blobs, blob_labels = make_blobs(n_samples=n_data, n_features=2,
- centers=n_centers, random_state=seed)
- clusters_blob = KMeans(n_clusters=n_centers, random_state=seed).fit_predict(blobs)
- # Generate data uniformly at random and run k-means
- uniform = np.random.rand(n_data, 2)
- clusters_uniform = KMeans(n_clusters=n_clusters,
- random_state=seed).fit_predict(uniform)
- # Matplotlib incantations for visualizing results
- figure = plt.figure()
- plt.subplot(221)
- plt.scatter(blobs[:, 0], blobs[:, 1], c=blob_labels, cmap='gist_rainbow')
- plt.title("(a) Four randomly generated blobs", fontsize=14)
- plt.axis('off')
- plt.subplot(222)
- plt.scatter(blobs[:, 0], blobs[:, 1], c=clusters_blob, cmap='gist_rainbow')
- plt.title("(b) Clusters found via K-means", fontsize=14)
- plt.axis('off')
- plt.subplot(223)
- plt.scatter(uniform[:, 0], uniform[:, 1])
- plt.title("(c) 1000 randomly generated points", fontsize=14)
- plt.axis('off')
- plt.subplot(224)
- plt.scatter(uniform[:, 0], uniform[:, 1], c=clusters_uniform, cmap='gist_rainbow')
- plt.title("(d) Clusters found via K-means", fontsize=14)
- plt.axis('off')
聚类作为表面平铺
聚类的常见应用假设存在自然聚类;即,在原本空白的空间中散布着密集数据区域。 在这些情况下,存在正确的聚类数量的概念,人们发明了聚类指数来衡量数据分组的质量,以便为k进行选择。
然而,当数据像图 7-2 (c)那样相当均匀地分布时,不再有正确的簇数。在这种情况下,聚类算法的作用是矢量量化,即将数据划分为有限数量的块。当使用量化向量而不是原始向量时,可以根据可接受的近似误差来选择簇的数量。
从视觉上看, k均值的这种用法可以被认为是用补丁覆盖数据表面,如图 7-3 所示。如果我们在瑞士卷数据集上运行k均值,这确实是我们得到的结果。

图 7-3。来自聚类算法的瑞士卷上的概念性局部补丁
示例 7-2使用 scikit-learn 在瑞士卷上生成噪声数据集,使用k均值对其进行聚类,并可视化使用 Matplotlib 的聚类结果。数据点根据其集群 ID 着色。
示例 7-2。瑞士卷上的 k 均值
>>> frommpl_toolkits.mplot3dimportAxes3D>>>fromsklearnimportmanifold,datasets# Generate a noisy Swiss roll dataset>>>X,color=datasets.samples_generator.make_swiss_roll(n_samples=1500)# Approximate the data with 100 k-means clusters>>>clusters_swiss_roll=KMeans(n_clusters=100,random_state=1).fit_predict(X)# Plot the dataset with k-means cluster IDs as the color>>>fig2=plt.figure()>>>ax=fig2.add_subplot(111,projection='3d')>>>ax.scatter(X[:,0],X[:,1],X[:,2],c=clusters_swiss_roll,cmap='Spectral')- from mpl_toolkits.mplot3d import Axes3D
- from sklearn import manifold, datasets
- # Generate a noisy Swiss roll dataset
- X, color = datasets.samples_generator.make_swiss_roll(n_samples=1500)
- # Approximate the data with 100 k-means clusters
- clusters_swiss_roll = KMeans(n_clusters=100, random_state=1).fit_predict(X)
- # Plot the dataset with k-means cluster IDs as the color
- fig2 = plt.figure()
- ax = fig2.add_subplot(111, projection='3d')
- ax.scatter(X[:, 0], X[:, 1], X[:, 2], c=clusters_swiss_roll, cmap='Spectral')
在这个例子中,我们在瑞士卷表面随机生成了 1,500 个点,并要求k -means 用 100 个簇来近似它。我们从帽子里取出数字 100,因为它看起来是一个相当大的数字来覆盖相当小的空间。结果(图 7-4)看起来不错;集群确实非常局部,流形的不同部分被映射到不同的集群。伟大的!我们完了吗?
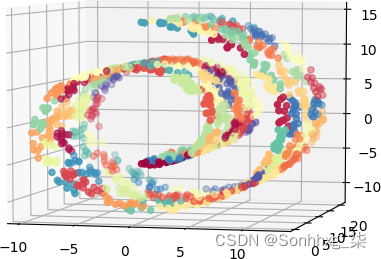
图 7-4。使用具有 100 个集群的 k-means 近似瑞士卷数据集
问题是,如果我们选择的k太小,那么从流形学习的角度来看,结果就不会那么好。图 7-5显示了k均值在具有 10 个簇的瑞士卷上的输出。我们可以清楚地看到来自流形的非常不同部分的数据被映射到相同的集群(例如,黄色、紫色、绿色和品红色集群——看,我们告诉过你插图最好是彩色的!)。
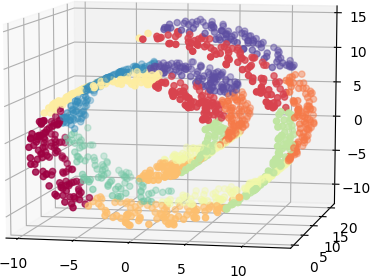
图 7-5。瑞士卷上的 k-means 有 10 个簇
如果数据在整个空间均匀分布,那么选择正确的k归结为球体填充问题。在d维中,可以容纳大约 1/ r d个半径为r的球体。每个k均值簇是一个球体,半径是用质心表示该球体中的点的最大误差。所以,如果我们愿意容忍每个数据点的最大近似误差r,那么聚类的数量就是O ( 1/r d ),其中d是数据原始特征空间的维数。
均匀分布是k均值的最坏情况。如果数据密度不均匀,那么我们将能够用更少的簇来表示更多的数据。一般来说,很难说出数据在高维空间中是如何分布的。可以保守一点,选择一个较大的k,但不能太大,因为k将成为下一步建模的特征数。
用于分类的 k-Means 特征化
当使用k -means 作为特征化过程时,数据点可以由其集群成员(集群成员分类变量的稀疏单热编码;参见“单热编码”)来表示,我们现在对此进行说明。
如果目标变量也可用,那么我们可以选择将该信息作为聚类过程的提示。合并目标信息的一种方法是简单地将目标变量作为附加输入特征包含到k均值算法中。由于目标是最小化所有输入维度上的总欧氏距离,因此聚类过程将尝试平衡目标值和原始特征空间中的相似性。可以缩放目标值以从聚类算法中获得或多或少的关注。目标的较大差异将产生更关注分类边界的聚类。
示例 7-3显示了一个简单的k均值特征化器。它被定义为可以适合训练数据并转换任何新数据的类对象。
示例 7-3。k -均值特征化器
- import numpy as np
- from sklearn.cluster import KMeans
- class KMeansFeaturizer:
- """Transforms numeric data into k-means cluster memberships.
- This transformer runs k-means on the input data and converts each data point
- into the ID of the closest cluster. If a target variable is present, it is
- scaled and included as input to k-means in order to derive clusters that
- obey the classification boundary as well as group similar points together.
- """
- def __init__(self, k=100, target_scale=5.0, random_state=None):
- self.k = k
- self.target_scale = target_scale
- self.random_state = random_state
- def fit(self, X, y=None):
- """Runs k-means on the input data and finds centroids.
- """
- if y is None:
- # No target variable, just do plain k-means
- km_model = KMeans(n_clusters=self.k,
- n_init=20,
- random_state=self.random_state)
- km_model.fit(X)
- self.km_model_ = km_model
- self.cluster_centers_ = km_model.cluster_centers_
- return self
- # There is target information. Apply appropriate scaling and include
- # it in the input data to k-means.
- data_with_target = np.hstack((X, y[:,np.newaxis]*self.target_scale))
- # Build a pre-training k-means model on data and target
- km_model_pretrain = KMeans(n_clusters=self.k,
- n_init=20,
- random_state=self.random_state)
- km_model_pretrain.fit(data_with_target)
- # Run k-means a second time to get the clusters in the original space
- # without target info. Initialize using centroids found in pre-training.
- # Go through a single iteration of cluster assignment and centroid
- # recomputation.
- km_model = KMeans(n_clusters=self.k,
- init=km_model_pretrain.cluster_centers_[:,:2],
- n_init=1,
- max_iter=1)
- km_model.fit(X)
- self.km_model = km_model
- self.cluster_centers_ = km_model.cluster_centers_
- return self
- def transform(self, X, y=None):
- """Outputs the closest cluster ID for each input data point.
- """
- clusters = self.km_model.predict(X)
- return clusters[:,np.newaxis]
- def fit_transform(self, X, y=None):
- self.fit(X, y)
- return self.transform(X, y)
为了说明使用之间的区别并且在示例 7-4中聚类时不使用目标信息,我们将特征化器应用于使用scikit-learn 的make_moons函数生成的合成数据集,并绘制聚类边界的 Voronoi 图。
示例 7-4。有和没有目标提示的 k-means 特征化
- from scipy.spatial import Voronoi, voronoi_plot_2d
- from sklearn.datasets import make_moons
- training_data, training_labels = make_moons(n_samples=2000, noise=0.2)
- kmf_hint = KMeansFeaturizer(k=100, target_scale=10).fit(training_data,
- training_labels)
- kmf_no_hint = KMeansFeaturizer(k=100, target_scale=0).fit(training_data,
- training_labels)
- def kmeans_voronoi_plot(X, y, cluster_centers, ax):
- """Plots the Voronoi diagram of the k-means clusters overlaid with the data"""
- ax.scatter(X[:, 0], X[:, 1], c=y, cmap='Set1', alpha=0.2)
- vor = Voronoi(cluster_centers)
- voronoi_plot_2d(vor, ax=ax, show_vertices=False, alpha=0.5)
图 7-6显示了结果的比较。数据集的两个卫星根据它们的类别标签着色。底部面板显示了在没有目标信息的情况下训练的集群。请注意,许多集群跨越了两个类之间的空白区域。顶部面板显示,当为聚类算法提供目标信息时,聚类边界沿类边界对齐得更好。
让我们测试一下k均值特征在分类方面的有效性。示例 7-5对使用k均值聚类特征扩充的输入数据应用逻辑回归。它将结果与具有径向基函数核 (RBF SVM)、k -最近邻 ( k NN) 的支持向量机进行比较,随机森林 (RF) 和梯度提升树 (GBT) 分类器。RF 和 GBT 是流行的非线性分类器,具有最先进的性能。RBF SVM 是一种合理的欧氏空间非线性分类器。k NN 根据其k个最近邻的平均值对数据进行分类。
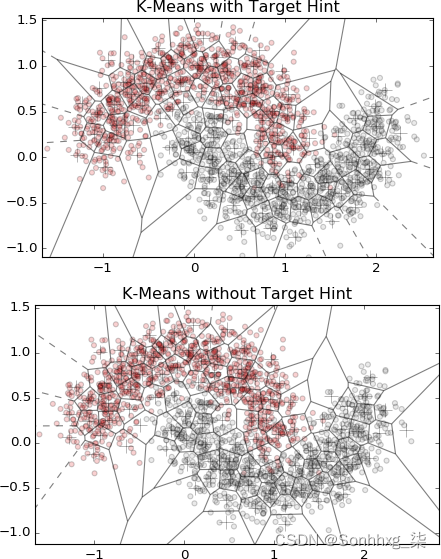
图 7-6。使用目标类信息的 k-means 聚类(上图)和不使用(下图)
分类器的默认输入数据由每个数据点的二维坐标组成。逻辑回归也给出了聚类成员特征(在图 7-7中标记为“LR with k - means” )。作为基线,我们还尝试仅在 2D 坐标(标记为“LR”)上进行逻辑回归。
示例 7-5。使用 k-means 聚类特征进行分类
- from sklearn.linear_model import LogisticRegression
- from sklearn.svm import SVC
- from sklearn.neighbors import KNeighborsClassifier
- from sklearn.ensemble import RandomForestClassifier, GradientBoostingClassifier
- ### Generate some test data from the same distribution as training data
- test_data, test_labels = make_moons(n_samples=2000, noise=0.3)
- ### Use the k-means featurizer to generate cluster features
- training_cluster_features = kmf_hint.transform(training_data)
- test_cluster_features = kmf_hint.transform(test_data)
- ### Form new input features with cluster features
- training_with_cluster = scipy.sparse.hstack((training_data,
- training_cluster_features))
- test_with_cluster = scipy.sparse.hstack((test_data, test_cluster_features))
- ### Build the classifiers
- lr_cluster = LogisticRegression(random_state=seed).fit(training_with_cluster,
- training_labels)
- classifier_names = ['LR',
- 'kNN',
- 'RBF SVM',
- 'Random Forest',
- 'Boosted Trees']
- classifiers = [LogisticRegression(random_state=seed),
- KNeighborsClassifier(5),
- SVC(gamma=2, C=1),
- RandomForestClassifier(max_depth=5, n_estimators=10, max_features=1),
- GradientBoostingClassifier(n_estimators=10, learning_rate=1.0,
- max_depth=5)]
- for model in classifiers:
- model.fit(training_data, training_labels)
- ### Helper function to evaluate classifier performance using ROC
- def test_roc(model, data, labels):
- if hasattr(model, "decision_function"):
- predictions = model.decision_function(data)
- else:
- predictions = model.predict_proba(data)[:,1]
- fpr, tpr, _ = sklearn.metrics.roc_curve(labels, predictions)
- return fpr, tpr
- ### Plot results
- import matplotlib.pyplot as plt
- plt.figure()
- fpr_cluster, tpr_cluster = test_roc(lr_cluster, test_with_cluster, test_labels)
- plt.plot(fpr_cluster, tpr_cluster, 'r-', label='LR with k-means')
- for i, model in enumerate(classifiers):
- fpr, tpr = test_roc(model, test_data, test_labels)
- plt.plot(fpr, tpr, label=classifier_names[i])
- plt.plot([0, 1], [0, 1], 'k--')
- plt.legend()
图 7-7显示了每个分类器在测试集上进行评估时的接收器操作特性 (ROC) 曲线。ROC 曲线显示了当我们改变分类决策边界时真阳性和假阳性之间的权衡。(有关详细信息,请参见 Zheng [2015]。)一个好的分类器应该快速达到高真阳性率和低误报率,因此向左上角急剧上升的曲线是好的。
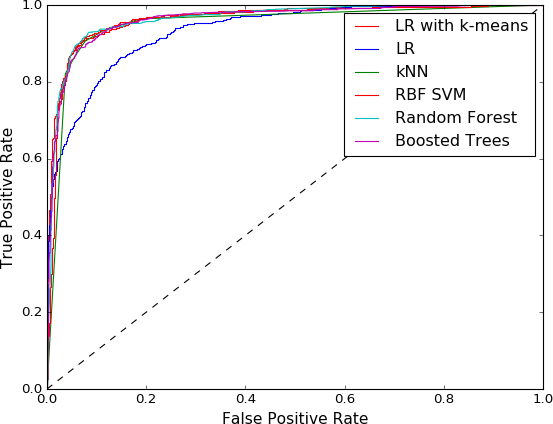
图 7-7。k 均值 + 逻辑回归与非线性分类器的 ROC 以及合成双月数据集上的简单逻辑回归
我们的图显示逻辑回归在有聚类特征的情况下比没有聚类特征时表现更好。事实上,对于聚类特征,线性分类器的性能与非线性分类器一样好。一个小警告是,在这个玩具示例中,我们没有调整任何模型的超参数。一旦模型完全调整,性能可能会有所不同,但至少这表明具有k均值的 LR 有可能与非线性分类器相提并论。这是一个不错的结果,因为线性分类器的训练成本比非线性分类器低得多。较低的计算成本允许我们在同一时间段内尝试更多具有不同特征的模型,这增加了最终得到更好模型的机会。
优点、缺点和陷阱
使用k均值将空间数据转换为特征是模型堆叠的一个示例,其中一个模型的输入是另一个模型的输出。堆叠的另一个例子是使用决策树类型模型(随机森林或梯度提升树)的输出作为线性分类器的输入。近年来,堆叠已成为一种越来越流行的技术。非线性分类器的训练和维护成本很高。堆叠的关键直觉是将非线性推入特征并使用非常简单的通常是线性的模型作为最后一层。特征化器可以离线训练,这意味着可以使用需要更多计算能力或内存但生成有用特征的昂贵模型。顶层的简单模型可以快速适应不断变化的在线数据分布。这是准确性和速度之间的一个很好的权衡,这种策略通常用于需要快速适应不断变化的数据分布的目标广告等应用程序。
与使用非线性分类器相比,k - means 与逻辑回归的训练和存储成本更低。表 7-1是一张图表,详细说明了许多机器学习模型在计算和内存方面的训练和预测复杂性。n表示数据点的数量,d表示(原始)特征的数量。
表 7-1。机器学习模型的复杂性 模型 时间 空间 k-means training O(nkd) O ( kd ) k-means predict O ( kd ) O ( kd ) LR + cluster features training O ( n ( d+k )) O ( d+k ) LR + cluster features predict O ( d+k ) O ( d+k ) RBF SVM training O ( n²d ) O ( n² ) RBF SVM predict O(sd) O(sd) GBT training O(nd2ᵐt) O(nd2ᵐt) GBT predict O(2ᵐt) O(2ᵐt) kNN training O(1) O(nd) kNN predict O ( nd + k log n ) O(nd) 流式k均值可以在时间O ( nd ( log k + log log n ) ) 内完成,这比大k的O ( nkd )快得多。
对于k均值,训练时间为O ( nkd ),因为每次迭代都涉及计算每个数据点和每个质心 ( k )之间的d维距离。我们乐观地假设迭代次数不是n的函数,尽管这可能并非在所有情况下都是正确的。预测需要计算新数据点与每个k质心之间的距离,即O ( kd )。对于k个质心的坐标,存储空间要求为O ( kd ) 。
逻辑回归训练和预测在数据点数量和特征维度上都是线性的。RBF SVM 训练很昂贵,因为它涉及计算每对输入数据的内核矩阵。RBF SVM 预测比训练成本更低;它与支持向量的数量s和特征维度d成线性关系。GBT培训和预测在数据大小和模型大小方面呈线性关系(t棵树,每棵树最多有 2 m个叶子,其中m是树的最大深度)。一个天真k NN的实现根本不需要训练时间,因为训练数据本身本质上就是模型。成本在预测时支付,其中输入必须针对每个原始训练点进行评估,并进行部分排序以检索k个最近的邻居。
总体而言,k -means + LR 是唯一在训练和预测时间都是线性的组合(相对于训练数据的大小O ( nd ) 和模型大小O ( kd ))。复杂度与 GBT 最为相似,其成本与数据点数量、特征维度和模型大小 ( O ( 2 m t )) 成线性关系。很难说k -means + LR 或 GBT 是否会产生更小的模型——这取决于数据的空间特征。
数据泄漏的可能性
那些记得我们关于数据泄漏的警告(参见“防止数据泄漏”)的人可能会问,在k均值特征化步骤中包含目标变量是否会导致这样的问题。答案是“是的”,但在箱计数的情况下不是那么多。如果我们使用相同的数据集来学习聚类和构建分类模型,那么有关目标的信息就会泄漏到输入变量中。因此,对训练数据的准确性评估可能会过于乐观,但在对保留验证集或测试集进行评估时,偏差会消失。此外,泄漏不会像二进制计数统计(参见“二进制计数”)那样严重,因为聚类算法的有损压缩会抽象掉一些信息。要格外小心防止泄漏,请提供一个单独的数据集来派生集群,就像在 bin 计数的情况下一样。
k均值特征化对于在空间中形成密集区域块的实值、有界数字特征很有用。团块可以是任何形状,因为我们可以增加簇的数量来近似它们。(与经典的集群设置不同,我们不关心发现集群的“真实”数量;我们只需要覆盖它们。)
k均值无法处理欧几里德距离没有意义的特征空间——即奇怪分布的数值变量或分类变量。如果特征集包含这些变量,那么有几种方法可以处理它们:
- 仅对实值、有界数字特征应用k均值特征化。
- 定义自定义指标以处理多种数据类型并使用k -medoids 算法。(k -medoids 类似于k -means但允许任意距离度量。)
- 将分类变量转换为分箱统计(参见“分箱计数”),然后使用k均值对它们进行特征化。
结合处理分类变量和时间序列的技术,k均值特征化可以适用于处理客户营销和销售分析中经常出现的那种丰富数据。由此产生的聚类可以被认为是用户细分,这是对下一步建模步骤非常有用的特征。
概括
本章使用一种有点非常规的方法来说明模型堆叠的概念:将受监督的k均值与简单的线性分类器相结合。k-均值通常用作无监督建模方法,以在特征空间中找到密集的数据点簇。然而,在这里,k -means 可以选择将类标签作为输入。这有助于k -means 找到更好地与类之间的边界对齐的集群。
我们将在下一章讨论的深度学习通过将神经网络层层叠加,将模型堆叠提升到一个全新的水平。最近 ImageNet 大规模视觉识别挑战赛的两个获胜者涉及 13 层和 22 层神经网络。他们利用大量未标记训练图像的可用性,并寻找产生良好图像特征的像素组合。 本章中的技术分别从线性分类器中训练k均值特征化器。但是可以联合优化特征化器和分类器。正如我们将要看到的,深度学习训练走的是后一种路线。
-
相关阅读:
k8s常用命令
Sui提供dApp Kit 助力快速构建React Apps和dApps
城市路边停车收费系统/停车收费管理系统
【正点原子Linux连载】第二十六章 APP主界面开发项目 摘自【正点原子】I.MX6U嵌入式Qt开发指南V1.0.2
Runnable和Callable啥时候用?
echarts-wordcloud ——文字云制作企业标签——基础积累
LQ0152 杨辉三角形【模拟】
黑马程序员微服务 分布式搜索引擎3
2.(vue3.x+vite)组件注册并调用
03-React网络通信(Axios, PubSubJs, Fetch)
- 原文地址:https://blog.csdn.net/sikh_0529/article/details/128039260