领悟《信号与系统》之 非周期信号的傅里叶变换及性质

这里记录的信号都是非周期信号的傅里叶变化，频谱变换的特点就是，时域信号无限长，则频谱有限；时域信号有限长，则频谱无限宽。和周期信号不一样的，非周期信号其实在周期信号上衍生出来的。

一、非周期信号的傅里叶变换

1、傅立叶正变换和逆变换

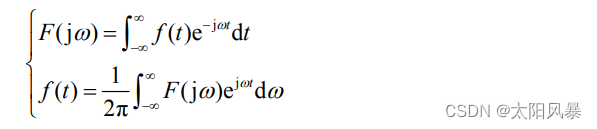
式中 F(jω) 称为 f(t) 的 频率密度函数 或简称 频谱函数。

• 表示形式如下：
  
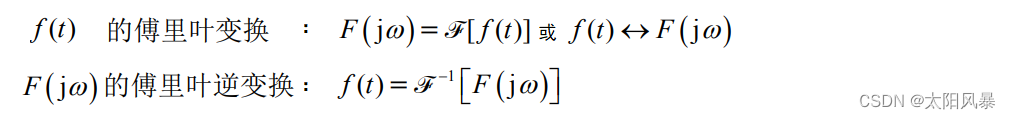
  2、频谱函数
  非周期信号的傅立叶逆变换表示为
  

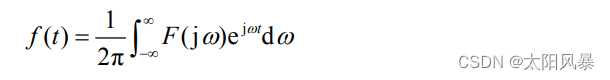
这表明非周期信号 f (t)可以由无穷多个指数函数 e^jωt 之加权和来表示，每个指数函数分量的大小为 1 / (2 * π) * F(jω) dω 这里的 F(jω) 不是振幅的概念，而是一个密度的概念，其量纲为单位频率的振幅，因而称其为频谱密度函数。 F(jω) 一般为复函数，
记为

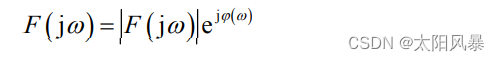
• |F(jω) | 为 F(jω) 的模，它代表信号 f (t)中各频率分量的相对大小
  将|F(jω) | ~ ω 的关系曲线称为非周期信号的幅度谱
• φ(ω) 为 F(jω) 的相位谱
  由 欧拉公式
  
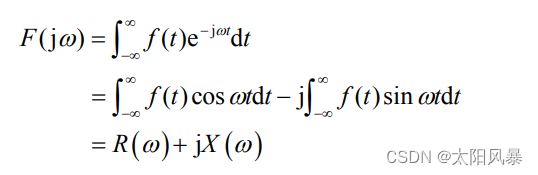
  推出：
  

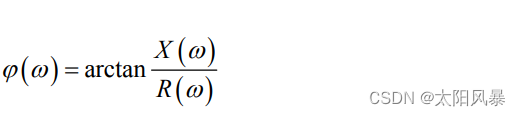
二、 典型信号的傅立叶变换

这里的傅里叶变换可以用性质公式推出来，但也可以用定义算出来，当然，性质公式的本质还是定义，我一般会推一遍性质公式，加深印象。

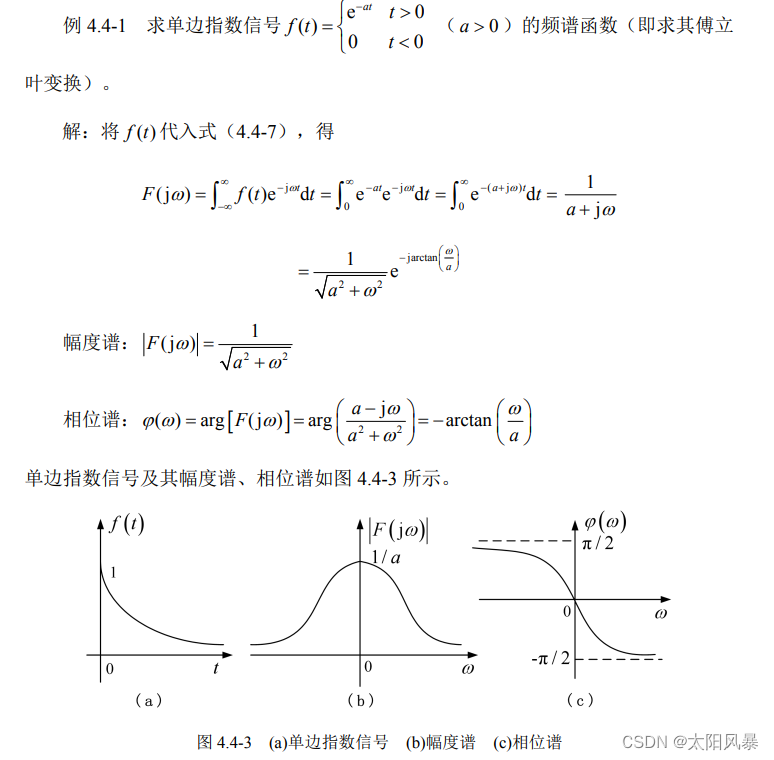
1.单边指数信号

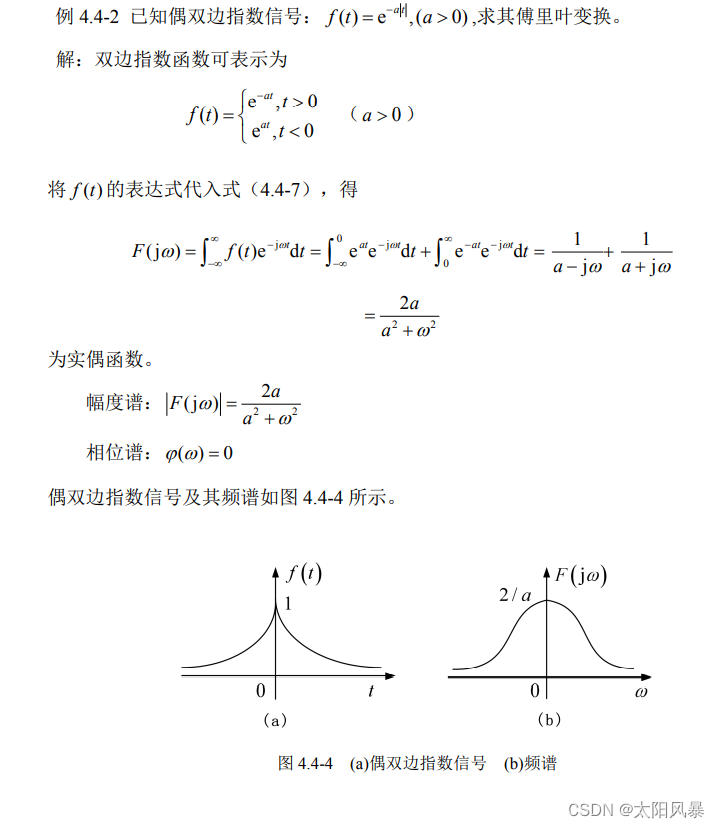
2.偶双边指数

3. 矩阵脉冲信号

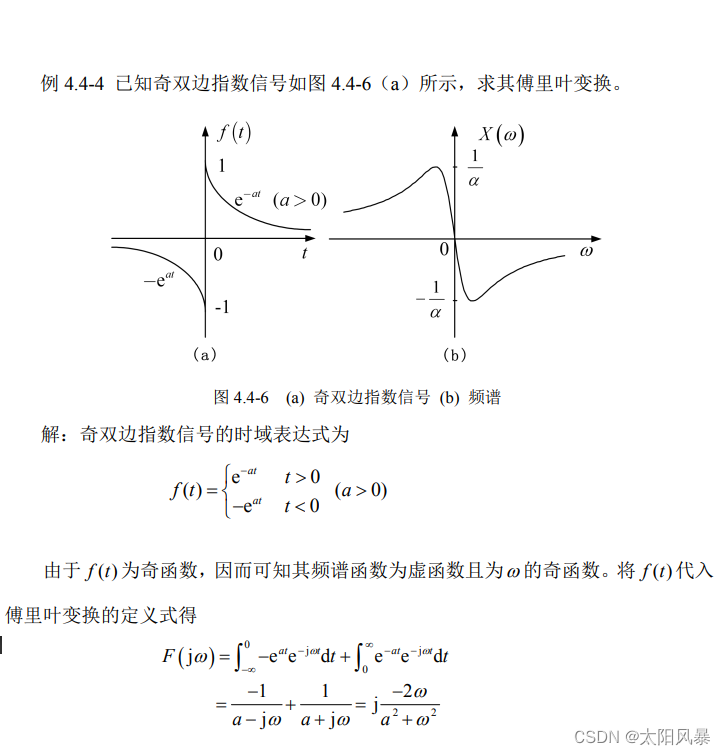
4. 奇双边指数

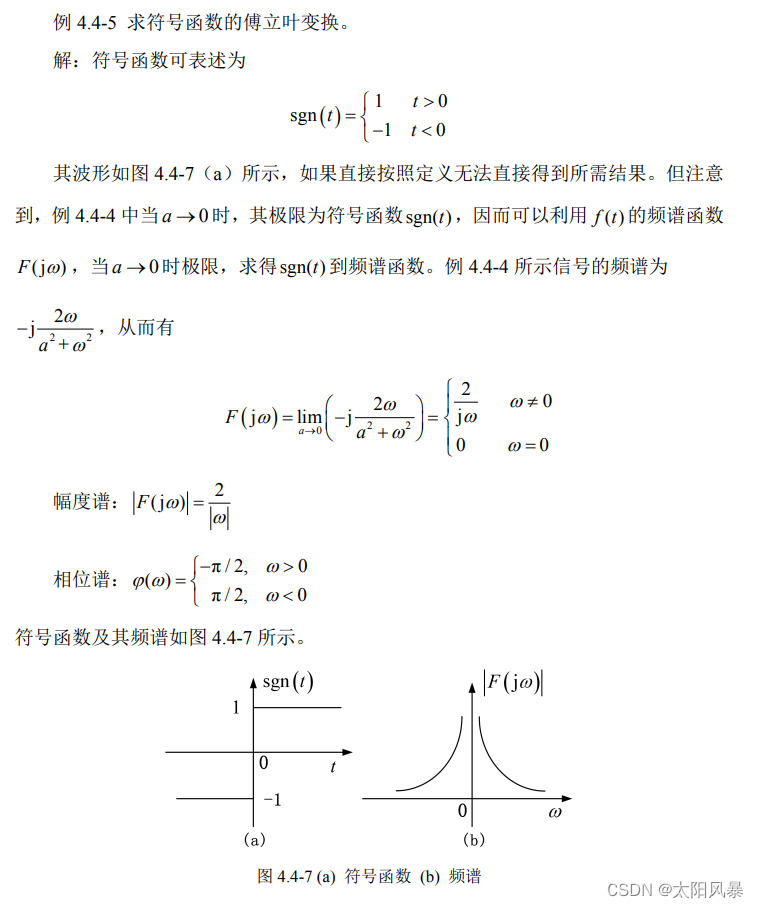
5. 符号函数

6. 冲激信号

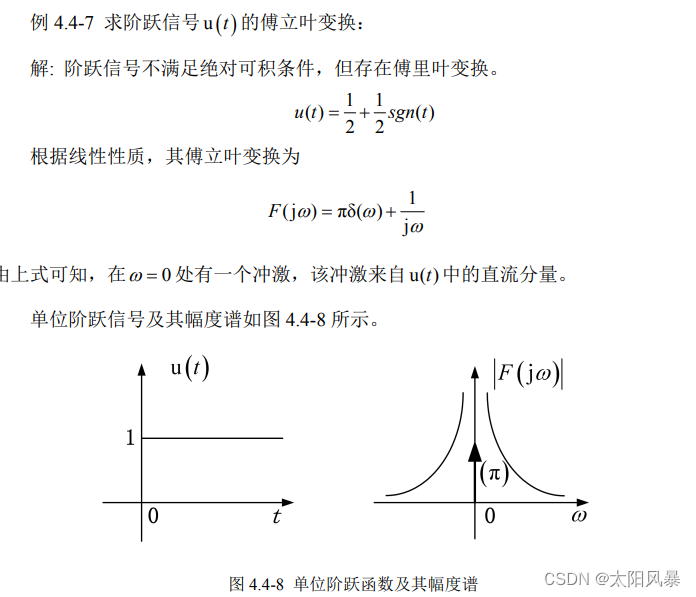
7. 阶跃信号

三、常用傅里叶变换表

觉得不错的，可以点个赞哦~