与分类有关的一种时序优先现象

(A，B)---2*30*2---(1,0)(0,1)

用网络分类A和B，让A由两张图片组成（0，0）（0，1），让B由两张图片组成（1，0）（0，0）,测试集由（0，0）（0，1）（1，0）（1，1）组成，记为网络0120，固定收敛误差统计迭代次数和分类准确率。得到表格.

统计收敛误差为5e-4时的分类情况

0，1，3都被分类为A，只有2被分类为B.因为A含有（0，1）B含有（1，0），因此（0，1）和（1，0）被分别分类为A和B。但在A和B中都有（0，0）.而且（0，0）相对A和B的两列的相似性都是100%，50%，（0，0）被分成A和B的概率应该是一样的。同样A和B的两列相对（1，1）的相似性都是0，50%，所以（1，1）被分成A和B的概率应该也是一样的，但为什么（0，0）（1，1）都被分成了A？

现在让A和B调换顺序，让A为（1，0）（0，0），让B是（0，0）（0，1），测试集同样是（0，0）（0，1）（1，0）（1，1），记为网络2001，同样统计迭代次数和分类准确率

统计收敛误差为5e-4时的分类情况

这时（0，0）（1，0）（1，1）被分成A，只有（0，1）被分成B。两个网络唯一的差别仅仅是进样的先后顺序不同，迭代次数是一致的

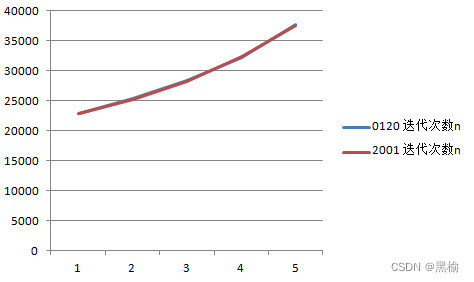
但分类结果却并不相同，（0，0）（1，1）在网络2001中被分成了（1，0）（0，0）.而在网络0120中被分成了（0，0）（0，1）。

所以这两个网络表达了一种时序优先现象，在存在时序优先的网络中如果一张图片被分成A和B的概率一致，则具体被分成A或B，决于A和B谁先进样。

这个实验也表明了差值结构相同的网络迭代次数相同

网络0120和2001的差值结构很容易通过左右变换和上下变换的方式实现转换。所以综合前述的实验，训练集AB的先后进样顺序可能对分类准确率产生影响，但不会影响迭代次数。而训练集中图片的先后顺序则对分类准确率和迭代次数都有影响。