【数据结构】二叉树的遍历

---

☀️二叉树的构建

便于理解二叉树的遍历，这里我们手动简单构建一个二叉树，当然，此处二叉树的构建并不是真正二叉树的构建方式，仅仅作为对本文所讲的二叉树遍历的一个参考。

代码如下：

typedef int BTDatatype;
typedef struct TreeNode
{
	BTDatatype data;
	struct TreeNode* left;
	struct TreeNode* right;
}BTNode;

BTNode* BuyBTNode(BTDatatype x)
{
	BTNode* newnode = (BTNode*)malloc(sizeof(BTNode));
	if (newnode == NULL)
	{
		perror("malloc fail");
		exit(-1);
	}
	newnode->data = x;
	newnode->left = NULL;
	newnode->right = NULL;
	return newnode;
}
int main()
{
	BTNode* n1 = BuyBTNode(1);
	BTNode* n2 = BuyBTNode(2);
	BTNode* n3 = BuyBTNode(3);
	BTNode* n4 = BuyBTNode(4);
	BTNode* n5 = BuyBTNode(5);
	BTNode* n6 = BuyBTNode(6);
	n1->left = n2;
	n2->left = n3;
	n1->right = n4;
	n4->left = n5;
	n4->right = n6;
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36

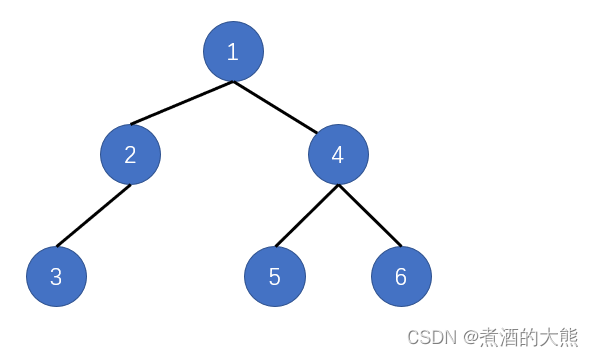
所构建的二叉树图如下所示：

☀️二叉树的遍历

🌻前序遍历

前序遍历也称为先根遍历，依次访问二叉树的根节点、左子树、右子树。

对本文所构建的二叉树进行前序遍历的顺序为：

1 -> 2 -> 3 -> NULL -> NULL -> NULL -> 4 -> 5 -> NULL -> NULL -> 6 -> NULL -> NULL

代码如下：

void PrevOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	printf("%d ", root->data);
	PrevOrder(root->left);
	PrevOrder(root->right);
}
1
2
3
4
5
6
7
8
9
10
11

结合本文所构建的二叉树运行的结果：

---

🌻中序遍历

中序遍历也称为中根遍历，依次访问二叉树的左子树、根节点、右子树。

对本文所构建的二叉树进行中序遍历的顺序为：

NULL -> 3 -> NULL -> 2 -> NULL -> 1 -> NULL -> 5 -> NULL -> 4 -> NULL -> 6 -> NULL

代码如下：

void InOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	InOrder(root->left);
	printf("%d ", root->data);
	InOrder(root->right);
}
1
2
3
4
5
6
7
8
9
10
11

结合本文所构建的二叉树运行的结果：

---

🌻后序遍历

中序遍历也称为后根遍历，依次访问二叉树的左子树、右子树、根节点。

对本文所构建的二叉树进行后序遍历的顺序为：

NULL -> NULL -> 3 -> NULL -> 2 -> NULL -> NULL -> 5 -> NULL -> NULL -> 6 -> 4 -> 1

代码如下：

void PostOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	PostOrder(root->left);
	PostOrder(root->right);
	printf("%d ", root->data);
}
1
2
3
4
5
6
7
8
9
10
11

结合本文所构建的二叉树运行的结果：

☀️完整代码展示

#include 
#include 
typedef int BTDatatype;
typedef struct TreeNode
{
	BTDatatype data;
	struct TreeNode* left;
	struct TreeNode* right;
}BTNode;

BTNode* BuyBTNode(BTDatatype x)
{
	BTNode* newnode = (BTNode*)malloc(sizeof(BTNode));
	if (newnode == NULL)
	{
		perror("malloc fail");
		exit(-1);
	}
	newnode->data = x;
	newnode->left = NULL;
	newnode->right = NULL;
	return newnode;
}
//前序遍历
void PrevOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	printf("%d ", root->data);
	PrevOrder(root->left);
	PrevOrder(root->right);
}
//中序遍历
void InOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	InOrder(root->left);
	printf("%d ", root->data);
	InOrder(root->right);
}
//后序遍历
void PostOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	PostOrder(root->left);
	PostOrder(root->right);
	printf("%d ", root->data);
}
int main()
{
	BTNode* n1 = BuyBTNode(1);
	BTNode* n2 = BuyBTNode(2);
	BTNode* n3 = BuyBTNode(3);
	BTNode* n4 = BuyBTNode(4);
	BTNode* n5 = BuyBTNode(5);
	BTNode* n6 = BuyBTNode(6);
	n1->left = n2;
	n1->right = n4;
	n2->left = n3;
	n4->left = n5;
	n4->right = n6;
	//前序遍历
	PrevOrder(n1);
	printf("\n");
	//中序遍历
	InOrder(n1);
	printf("\n");
	//后序遍历
	PostOrder(n1);
	printf("\n");
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83