初阶数据结构学习记录——열 二叉树（3）链式

目录

一、搜索二叉树的四种遍历方法(前中后层)

二、从代码角度理解搜索二叉树

三、难题解决

1、求二叉树节点个数 

2、求树的深度（高度）

3、求第k层的节点个数 k >= 1

4、查找值为x的节点

---

链式二叉树是由指针形成的二叉树，之前写的二叉树是由数组组成的，链式由链表来做。链式二叉树每个节点有两个指针，指向两边。以往二叉树，栈，队列等等都需要增删查改，但链式二叉树则不是这样，是因为由于链表结构，它没办法很好地增删查改。所以这里要写的并不是和数组二叉树一样的结构，而是一颗搜索树，左子树比根节点小，右子树比根节点大。这样插入一个数值就可以找到安放的位置，想要搜索某个数也可以选择一颗来往下查找，这样查找的效率是树的高度次，搜索二叉树也就有了增删查改的意义，以及也可以进行遍历了。像之前写的二叉树能用来遍历，但也没有任何意义，而搜索二叉树则可以展示两个子树各自的情况。

一、搜索二叉树的四种遍历方法(前中后层)

前中后序（根）以及层序遍历

搜索二叉树一个思路就是一个根节点只管自己的两个子节点，其他一概不管。

关于前序，顺序为根，左子树，右子树：1 2 3 NULL NULL NULL 4 5 NULL NULL 6 NULL NULL。

分析一下这个前序，从根走起，然后再走左子树，也就是1 2 ，之后走到3，3的左子树是NULL，那么再看3的右子树，也是NULL，那么3这里就结束了，出现了两个NULL，回到2，3是2的左子树，那么再看2的右子树，是NULL，回到1，所有出现了1 2 3 NULL NULL NULL。那么再访问1的右子树，4，访问左子树5，5的左右子树都是NULL，所以有 4 5 NULL NULL，再看6，6后面也是两个NULL，所以最后整个顺序就出来了。

关于中序，顺序为左子树，根，右子树：NULL 3 NULL 2 NULL 1 NULL 5 NULL 4 NULL 6 NULL

关于后序，顺序为左子树，右子树，根：NULL NULL 3 NULL 2  NULL NULL 5 NULL NULL 6 4 1

关于层序，从第一层开始，每层从左到右，一层层访问：1 2 4 3 5 6

二、从代码角度理解搜索二叉树

这个二叉树由链表构成，所以

typedef int BTDataType;
typedef struct BinaryTreeNode
{
    BTDataType data;
    struct BinaryTreeNode* left;
    struct BinaryTreeNode* right;
}BTNode;

搜索二叉树的实现会用到递归。遍历时，整个数的根节点和它的子节点遍历完后，再以子节点为根节点，继续向下遍历，所以整体用递归更适合。

我们先写前序遍历。如果root本身就为空，那么就把直接返回空；不为空的情况下，由于顺序为根，左子树，右子树，那么我们需要先打印一下根节点元素，然后左下走，如果左面走完了再走右面，然后我们还得回来再走整个数的右子树。代码如下：

void PrevOrder(BTNode* root) 
{
    if (root == NULL) 
    {
        printf("NULL ");
        return;
    }
 
    printf("%d ", root->data);
    PrevOrder(root->left);
    PrevOrder(root->right);
}

尽量画图理解递归过程，这里就不写了。呈现出来有点麻烦。

我们先测试一下，写个创建结构体函数，并写出关系来测试。

BTNode* BuyBTNode(BTDataType x)
{
    BTNode* node = (BTNode*)malloc(sizeof(BTNode));
    if (node == NULL)
    {
        perror("malloc fail");
        exit(-1);
    }
 
    node->data = x;
    node->left = node->right = NULL;
    return node;
}
 
int main()
{
    BTNode* n1 = BuyBTNode(1);
    BTNode* n2 = BuyBTNode(2);
    BTNode* n3 = BuyBTNode(3);
    BTNode* n4 = BuyBTNode(4);
    BTNode* n5 = BuyBTNode(5);
    BTNode* n6 = BuyBTNode(6);
 
    BTNode* n7 = BuyBTNode(7);
    n3->right = n7;
 
    n1->left = n2;
    n1->right = n4;
    n2->left = n3;
    n4->left = n5;
    n4->right = n6;
 
    PrevOrder(n1);
    printf("\n");
    return 0;
}

结果如下

 

 所以接下来中序，后序也都好写了。

void InOrder(BTNode* root)
{
    if (root == NULL)
    {
        printf("NULL ");
        return;
    }
 
    InOrder(root->left);
    printf("%d ", root->data);
    InOrder(root->right);
}
 
void PostOrder(BTNode* root)
{
    if (root == NULL)
    {
        printf("NULL ");
        return;
    }
 
    PostOrder(root->left);
    PostOrder(root->right);
    printf("%d ", root->data);
}

三、难题解决

1、求二叉树节点和叶节点个数

能够很快想到的办法就是遍历一遍，数出节点个数，不是NULL就size++一次。但是我们不能像下面这样写

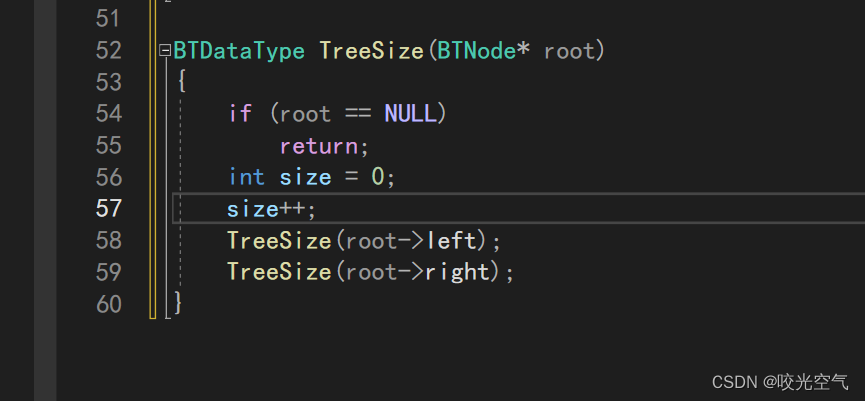
 每一次递归，都会开一块栈帧，每一块空间size都为0，所以最后根本不是我们要的结果。那如果static一下如何？static int size，size在静态区，确实不会受递归影响，但是同样也不受我们控制了，当多次调用后，size会一直加下去，也不是我们要的数字。不过size可以定义成全局变量，每次调用前都设为0，不过这个办法也有点麻烦。

关于计算节点个数，同样也可以用之前的思路，一个根节点管两个子节点，为空就0，不为空就传回来数字

int TreeSize(BTNode* root)
{
    return root == NULL ? 0 : TreeSize(root->left) + TreeSize(root->right) + 1;
}

 画图就能理解这个代码

增加一下难度，求叶子节点的个数

虽然这个问题的思路和之前异曲同工，但是不能这样写

程序最终会停在那里，然后直接退出。这是为什么？我们就着这个图再看

1的两个子节点都不是空，找到2，2同样也不是叶节点，找到3，3是叶节点，返回1，再回到2，访问2的右子节点，这时候就出问题了，本身这个节点就是NULL，然后程序还在判断它的左右子节点为不为空，程序就崩了。

所以我们必须要在判断左右前先判空

int TreeLeafSize(BTNode* root)
{
    if (root == NULL)
    {
        return 0;
    }
 
    if (root->left == NULL
        && root->right == NULL)
    {
        return 1;
    }
 
    return TreeLeafSize(root->left)
        + TreeLeafSize(root->right);
}

这样整个代码就对了。 测试代码

    printf("TreeSize:%d\n", TreeSize(n1));
    printf("TreeLeafSize:%d\n", TreeLeafSize(n1));

 

2、求树的深度（高度）

默认根从1开始。

先把原先的图增加一层

左右子树并不一定同样高度，我们就需要算出两个高度，比较出大的那个再+1，因为如果是空树，高度也也应当是1，如果是两层的，那么就需要求出哪个子树高度更高，再+1，就是整体的高度。

从2这棵子树开始走，到达7后，7的左右子树高度都为0，所以返回1，那么7这棵树的高度就是1，也就是3的右子树的高度，3的左子树返回0，那么3这棵树返回的高度就是1+1 = 2，也就是2的左子树的高度，2的右子树高度为0，那么2这棵树返回3，4这棵树同理，会返回2，3 > 2，所以1会收到3 + 1 = 4，所以这棵树的高度就是4。

int TreeHeight(BTNode* root)
{
    if (root == NULL)
    {
        return 0;
    }
 
    int leftHeight = TreeHeight(root->left);
    int rightHeight = TreeHeight(root->right);
    return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;
}

 测试代码

void TestTree2()
{
    BTNode* n1 = BuyBTNode(1);
    BTNode* n2 = BuyBTNode(2);
    BTNode* n3 = BuyBTNode(3);
    BTNode* n4 = BuyBTNode(4);
    BTNode* n5 = BuyBTNode(5);
    BTNode* n6 = BuyBTNode(6);
    BTNode* n7 = BuyBTNode(7);
    BTNode* n8 = BuyBTNode(8);
    BTNode* n9 = BuyBTNode(9);
    BTNode* n10 = BuyBTNode(10);
    BTNode* n11 = BuyBTNode(11);
    n1->left = n2;
    n1->right = n4;
    n2->left = n3;
    n3->right = n7;
    n3->left = n8;
    n4->left = n5;
    n4->right = n6;
    n5->left = n10;
    n10->right = n11;
    
    int size = TreeHeight(n1);
    printf("%d\n", size);
}

3、求第k层的节点个数 k >= 1

其实也是要分左右子树，但是和层序没有关系，这个题不需要层序。这里提供一个想法，第k层是相对于第1层的第k层，那对于第2层来说，那就是第k-1层，第k层的节点个数就等于根节点的左子树的第k-1层节点个数 +  根节点的右子树的第k-1层节点个数。遇到NULL就返回0。如果k为1，一个是本身就统计的祖先层，一个是相对来说是第一层，意思就程序已经来到第k层，那么这时候就相对来说是第1层，返回1。

int TreeKLevelSize(BTNode* root, int k)
{
    if (root == NULL)
        return 0;
 
    if (k == 1)
        return 1;
 
    // k > 1 子树的k-1
    return TreeKLevelSize(root->left, k - 1)
        + TreeKLevelSize(root->right, k - 1);
}

 测试代码，连同之前的。

int main()
{
    BTNode* n1 = BuyBTNode(1);
    BTNode* n2 = BuyBTNode(2);
    BTNode* n3 = BuyBTNode(3);
    BTNode* n4 = BuyBTNode(4);
    BTNode* n5 = BuyBTNode(5);
    BTNode* n6 = BuyBTNode(6);
    BTNode* n7 = BuyBTNode(7);
    n1->left = n2;
    n1->right = n4;
    n2->left = n3;
    n3->right = n7;
    n4->left = n5;
    n4->right = n6;
 
    PrevOrder(n1);
    printf("\n");
 
    InOrder(n1);
    printf("\n");
 
    PostOrder(n1);
    printf("\n");
 
    printf("TreeSize:%d\n", TreeSize(n1));
    printf("TreeLeafSize:%d\n", TreeLeafSize(n1));
    printf("TreeHeight:%d\n", TreeHeight(n1));
    printf("TreeKLevelSize:%d\n", TreeKLevelSize(n1, 3));
    return 0;
}

 我们还是用上面那个白图。

最终结果就是3。

4、查找值为x的节点

当然，还是递归。不过经历上面的问题，可以发现，关于具体数值的问题，我们就不能直接递归，需要在递归过程中用一个变量存储值才行。这个问题同样如此。

BTNode* TreeFind(BTNode* root, BTDataType x)
{
    if (root == NULL)
        return NULL;
    if (root->data == x)
        return root;
    BTNode* ret1 = TreeFind(root->left, x);
    if (ret1)
        return ret1;
    BTNode* ret2 = TreeFind(root->right, x);
    if (ret2)
        return ret2;
    return NULL;
}

根据以上问题，慢慢理解二叉树的结构。

结束。