图神经网络关系抽取论文阅读笔记（三）

1 用于关系提取的注意引导图卷积网络（Attention Guided Graph Convolutional Networks for Relation Extraction，2020）

论文：Attention Guided Graph Convolutional Networks for Relation Extraction，2020

1.1 引言

依赖树传递丰富的结构信息，这些信息对于提取文本中实体之间的关系非常有用。然而，如何有效利用相关信息而忽略依赖树中的无关信息仍然是一个具有挑战性的研究问题。现有的方法使用基于规则的硬剪枝策略来选择相关的部分依赖结构，可能并不总是产生最佳结果。在这项工作中，我们提出了注意引导图卷积网络(AGGCNs)，**这是一种直接以全依赖树作为输入的新模型。我们的模型可以理解为一种软修剪方法，自动学习如何有选择地关注对关系提取任务有用的相关子结构。**在包括跨句n元关系提取和大规模句子级关系提取在内的各种任务上的大量结果表明，我们的模型能够更好地利用全依赖树的结构信息，其结果显著优于以前的方法。

1.2 创新点

• 提出了一种新的AGGCNs，它以端到端方式学习“软修剪”策略，学习如何选择和丢弃信息。结合密集连接，AGGCN模型能够学习更好的图表示。
• 与之前的GCN比，模型实现了当时最好的关系抽取结果，不需要额外的计算，与树结构模型(例如，LSTM)不同，它可以有效地并行应用于依赖树。

AGGCNs（注意引导图卷积网络）：

• 输入：全依赖树（ full dependency trees）
• 特点：端到端、≈软剪枝方法（基于规则的硬剪枝会消除树中的部分重要的信息，给所有边分配权重，权重以端到端的形式学习得到–>自动学习剪枝）、自动学习如何有选择地关注对re有用的相关子结构、效果好、可并行地用于依赖树

• GCN+dense connection
  • 目的：对一个大的全连通图进行编码
  • 可得到局部和非局部依赖信息
  • 2层GCN效果最好（经验）
  • 可以学到更好的图形表示
• 可用于
  • n元关系提取
  • 大规模句子级别语料
  • 效果更好

1.3 之前方法的弊端

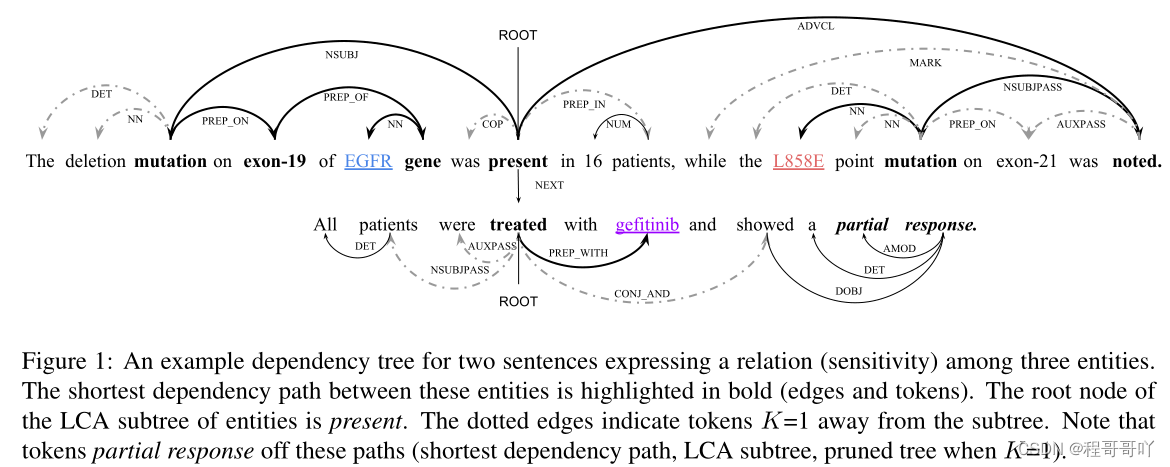
• 硬剪枝：
  • 基于规则的修剪策略可能会消除整个树中的一些重要信息
• 所以提出自动学习的软剪枝。
• 关系抽取的模型可以分为两类：
  • sequence-based（基于序列的）
    • 只对单词序列进行操作(Zeng et al.,2014; Wang et al., 2016)
  • dependency-based（基于依赖的）
    • 然而基于依赖的模型将依赖树合并到模型中(Bunescu和Mooney, 2005;Peng等人，2017)
    • 依赖树+剪枝
    • 比较：与基于顺序的模型相比，基于依赖的模型能够捕获仅从表面形式难以理解的非局部句法关系(Zhang et al.， 2018)。
• 剪枝策略（硬剪枝）：
  • Xu等人(2015b,c)只在全树实体之间的最短依赖路径上应用神经网络。
  • Miwa和Bansal(2016)将整个树缩减为实体的最低共同祖先(LCA)之下的子树。
  • Zhang等(2018)将 (GCNs) (Kipf and Welling, 2017)模型应用于修剪过的树。这棵树包含从LCA子树的依赖路径到K的标记。

1.4 AG-GCN

• AGGCN模型显示了一个示例语句及其依赖树。它由M个相同的块组成，每个块有三种层，如图所示：注意引导层、密集连接层、线性组合层
• 输入：每个块以表示图的节点嵌入和邻接矩阵作为输入。
• 注意引导层：multi-head attention：然后利用左下所示的多头注意构造N个注意引导邻接矩阵。
  • 原始的依赖树被转换成N个不同的完全连接的边加权图(为了简化，省略了自循环)。
  • 靠近边的数字表示矩阵中的权值。
• 密集连接层得到的矩阵被送入N个单独的dense connection的层，产生新的表示。
  • 左上角显示了一个密集连接层的例子，其中子层的数量(L)是3 (L是超参数)。
  • 每个子层将所有前面的输出连接起来作为输入。
• 线性组合层：最后，应用线性组合将N个紧密连接的层的输出组合成隐藏的表示。

1.4.1 GCN

GCNs是直接作用于图结构的神经网络(Kipf和Welling, 2017)。工作原理如下：

• 图：给出一个有n个节点的图，我们可以用一个n×n邻接矩阵A来表示图。

• 加方向：使得GCNs对依赖树进行编码。(Marcheggiani和Titov(2017))

  • 它们为树中的每个节点添加一个自循环。
  • 还包括一个依赖弧的反方向，即
    • 边i->j：有则$${\mathbf{A}}_{ij}=1\text{ and }{\mathbf{A}}_{ji}=1$$；无则$${\mathbf{A}}_{ij}=0\text{ and }{\mathbf{A}}_{ji}=0$$

• l层节点i的卷积运算如下：
  $${\mathbf{h}}_i^{(l)}=\rho \left(\sum _{j=1}^n{\mathbf{A}}_{ij}{\mathbf{W}}^{(l)}{\mathbf{h}}_j^{(l-1)}+{\mathbf{b}}^{(l)}\right)$$
  其中A为图的邻接矩阵，h为输入，w为权重矩阵，b为偏置向量，p为激活函数(Relu)

1.4.2 自注意力机制

自注意机制原型：$$\mathrm{Attention}(Q,K,V)=\mathrm{softmax}\left(\frac{Q{K}^T}{\sqrt{d_k}}\right)V$$

三个需要训练的矩阵:Q: query，要去查询的；K: key，等着被查的；V: value，实际的特征信息

1.4.3 多头注意力机制

一组q,k,v得到了一组当前词的特征表达；通过不同的head得到多个特征表达；将所有特征拼接在一起；可以通过再一层全连接来降维

1.4.4 Attention Guided Layer

该文我们没有使用基于规则的剪枝，而是在注意引导层开发了一种“软剪枝”策略，它为所有边缘分配权重。这些权重可以由模型以端到端方式学习。

注意力引导层：将一个树->多个全连接有权图：

方法：构造注意引导邻接矩阵A

• self-attention mechanism (Cheng et al., 2016)来得到A

  • 可以捕获单个序列的任意位置之间的交互。

• 本文:用multi-head attention 计算

  • 它允许模型联合处理来自不同表示子空间的信息
  • 计算：包括一个查询和一组键值对
  • 输出：计算为值的加权和，其中的权重：由具有相应键的查询函数计算。

• 多头注意力机制计算公式：
  $${\tilde{\mathbf{A}}}^{(\mathbf{t})}=\mathrm{softmax}\left(\frac{Q{\mathbf{W}}_i^Q\times {\left(K{\mathbf{W}}_i^K\right)}^T}{\sqrt{d}}\right)$$
  其中Q,K:等于AGGCN的h(l−1)，t:第t个attentionhead，共有N个（超参数)

• A~和A尺寸相同，所以没有增加计算消耗

• 关键思想：使用注意力来诱导节点之间的关系；特别是那些通过间接的多跳路径连接的节点

总结：将原始邻接矩阵转换为多个注意引导邻接矩阵。因此，输入依赖树被转换成多个完全连接的边缘加权图。在实践中，我们将原始邻接矩阵作为初始化处理，以便在节点表示中捕获依赖项信息，以便以后进行注意计算。注意力引导层从第二个块开始。

1.4.5 Densely Connected Layer

• 将稠密连接(Huang et al.， 2017)引入AGGCN模型，

• 目的：在大图上捕获更多的结构信息。

• 在密集连接的帮助下，我们能够训练更深的模型，

• 允许捕获丰富的局部和非局部信息，从而学习更好的图表示。

• 直接连接从任何层引入到它前面的所有层。$${\mathbf{g}}_j^{(l)}=\left[{\mathbf{x}}_j;{\mathbf{h}}_j^{(1)};\dots ;{\mathbf{h}}_j^{(l-1)}\right]$$

• 

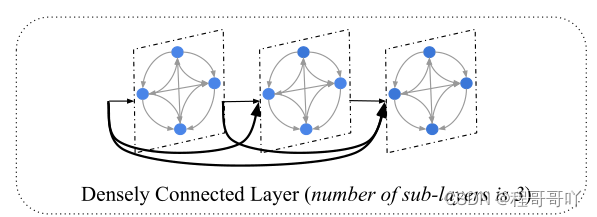
超参数：L子层，子层的维度：输入维度d和L共同决定$${\mathrm{d}}_{\text{hidden }}=\mathrm{d}/\mathrm{L}$$；

输出：每个子层的输出又会被连接起来->仍是d维；随子层数增加而缩小隐层size–>提高效率

与隐藏维度大于或等于输入维度的GCN模型不同，AGGCN模型随着层数的增加而缩小隐藏维度，以提高与DenseNets类似的参数效率(Huang et al.， 2017)。

• N个注意力头–>N个分离的densely connection

  从原来的：
  $${\mathbf{h}}_i^{(l)}=\rho \left(\sum _{j=1}^n{\mathbf{A}}_{ij}{\mathbf{W}}^{(l)}{\mathbf{h}}_j^{(l-1)}+{\mathbf{b}}^{(l)}\right)$$
  变成：
  $${\mathbf{h}}_{t_i}^{(l)}=\rho \left(\sum _{j=1}^n{\tilde{\mathbf{A}}}_{ij}^{(t)}{\mathbf{W}}_t^{(l)}{\mathbf{g}}_j^{(l)}+{\mathbf{b}}_t^{(l)}\right)$$

1.4.6 Linear Combination Layer

线性组合层，用于集成来自N个不同密连接层的表示。形式上，线性组合层的输出定义为:
$${\mathbf{h}}_{comb}={\mathbf{W}}_{comb}{\mathbf{h}}_{\text{out }}+{\mathbf{b}}_{comb}$$
其中$${\mathbf{h}}_{\text{out }}=\left[{\mathbf{h}}^{(1)};\dots ;{\mathbf{h}}^{(N)}\right]\in {\mathbb{R}}^{d\times N}$$

1.5 用于关系提取的AGGCNs

在依赖树上应用AGGCN模型之后，我们获得了所有令牌的隐藏表示。根据这些表示，关系提取的目标是预测实体之间的关系。接下来(Zhang et al.， 2018)，我们将句子表示和实体表示连接起来，得到最终的分类表示。

• 首先，我们需要获得h_sent句子表示。它可以被计算为:$$h_{\text{sent }}=f\left({\mathbf{h}}_{\text{mask }}\right)=f(\mathrm{AGGCN}(\mathbf{x}))$$
• $$f:{\mathbb{R}}^{d\times n}\to {\mathbb{R}}^{d\times 1}$$是一个Max池函数，它从n个输出向量映射到1个句子向量。
• 相似地得到实体表示：$$h_{e_i}=f\left({\mathbf{h}}_{{\mathbf{e}}_{\mathbf{i}}}\right)$$，第i个实体的隐层表示
• 由前馈神经网络得到最终表示（连接实体表示和句子表示）：$$h_{\text{final }}=\mathrm{F}\mathrm{F}\mathrm{N}\mathrm{N}\left(\left[h_{\text{sent }};h_{e_1};\dots h_{e_i}\right]\right)$$；最终表示输入到logistic regression classifier分类器中做预测。

1.6 实验

1.6.1 数据集

评估了该模型在两个任务上的性能，即

• 跨句n元关系提取：PubMed
• 句子级关系提取：1.TACRED数据集(收费）(Zhang et al., 2018)、2. Semeval-10 Task 8 (Hendrickx et al., 2010)

1.6.2 实验效果

n-ary：跨句n元关系提取

能用图卷积从树中得到更多信息，比GCN好，因为：

1. densely connection，使之可在大图中信息传递，使之可有效地学习到长距离依赖
2. attention，可筛去噪音，得到相关信息
3. 本文的模型可从全树中得到更好的表达

句子级（TACRED）

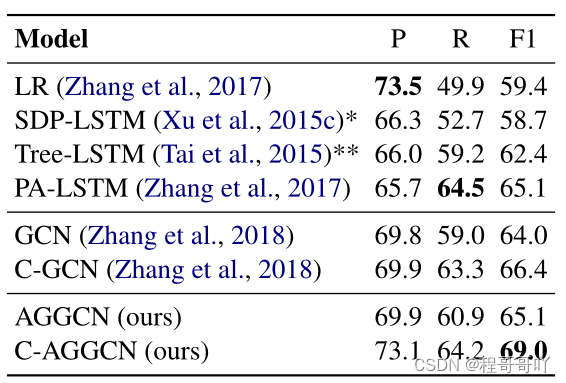
可以观察到AGGCN比GCN多1.1个F1点。推测这种有限的改进是由于缺乏有关词序或消歧的上下文信息。

句子级SemEval

在与(Zhang et al.， 2018)相同的设置下，在SemEval数据集上评估我们的模型(Zhang et al.， 2018)。结果如表3所示。这个数据集比TACRED小得多(仅为TACRED的1/10)。C-AGGCN模型(85.7)始终优于C-GCN模型(84.8)，具有良好的泛化能力

1.7 总结

我们介绍了一种新的注意引导图卷积网络(AGGCNs)。实验结果表明，AGGCNs在各种关系提取任务中都取得了先进的结果。

与以前的方法不同，AGGCNs直接操作整个树，并学习以端到端方式从树中提取有用的信息。

1.8 个人点评

本文最大的创新就是把整个句子的语法依存树作为输入，不修剪任何信息，从而达到用图神经网络做特征表示的效果，使得模型可以端到端方式从树中提取有用的信息，巧妙使用多头注意力机制和精密连接方法作为特征提取过度，整体模型还是比较复杂，编码难度较大。