神经网络和深度学习-后向传播back propagation

反向传播back propagation

首先我们要了解，前向传播，损失函数这些前置知识，下面我们给出一张神经网络的图

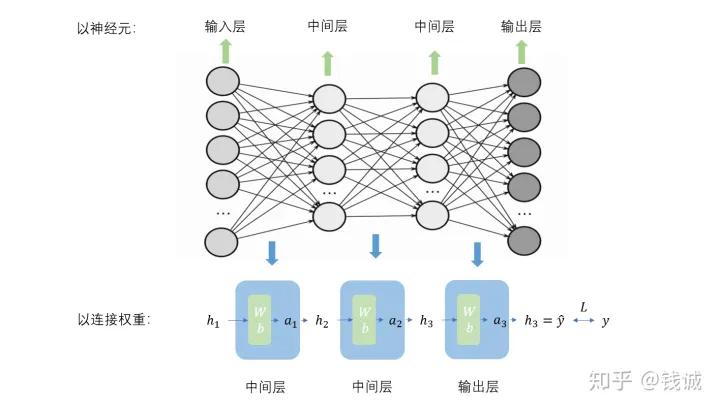
反向传播通过导数链式法则计算损失函数对各参数的梯度，并根据梯度进行参数的更新

下面举个简单的例子

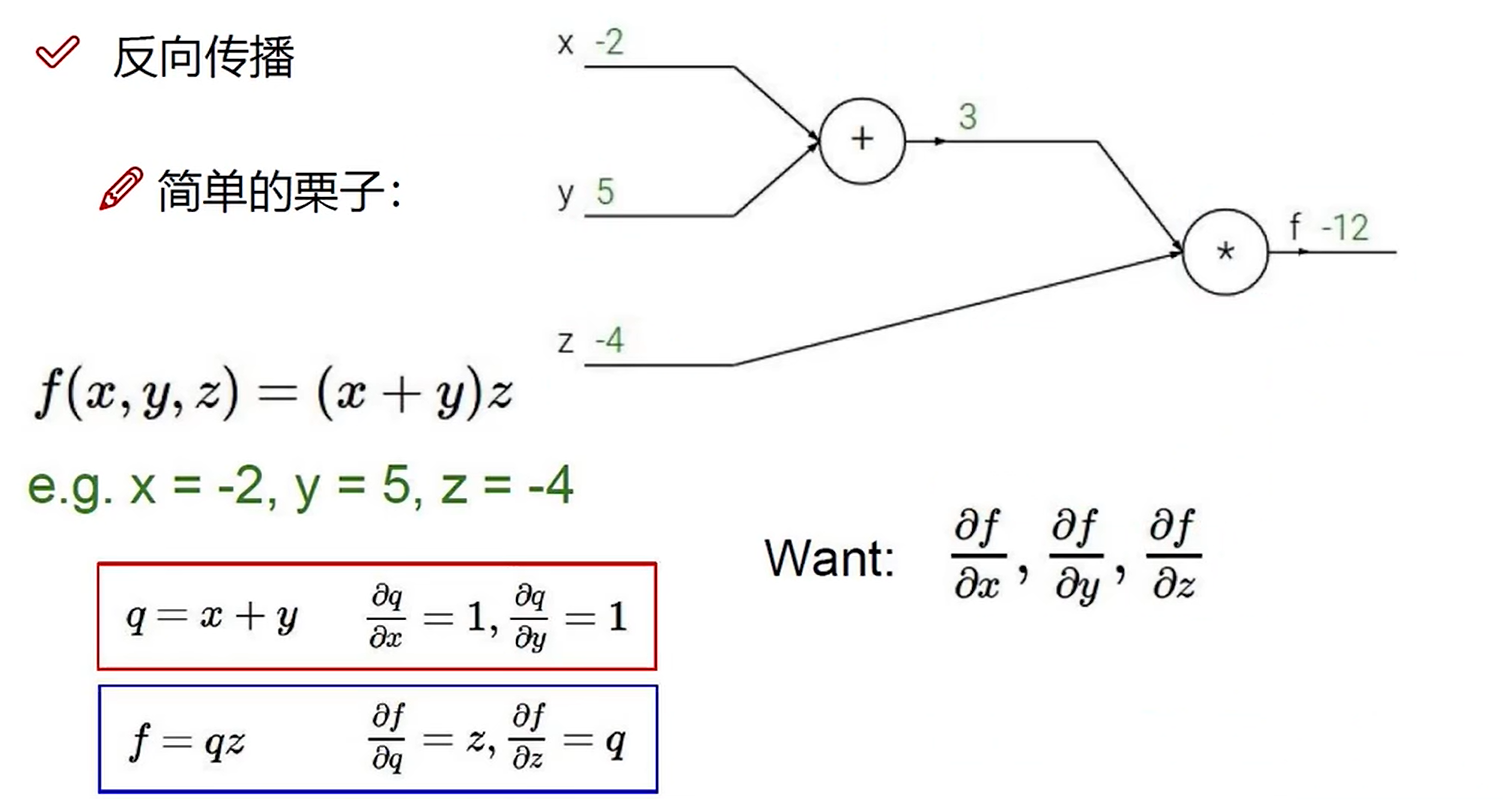
我们需要知道x,y,z分别对该模型有什么影响，故分别对他们求偏导

其中q = x+y，需要先对q求偏导，在对x和y进行求偏导**（链式求导法则）** ​

$$\frac{\partial f}{\partial x}=\frac{\partial f}{\partial q}\cdot \frac{\partial q}{\partial x}$$

$$\frac{\partial f}{\partial y}=\frac{\partial f}{\partial q}\cdot \frac{\partial q}{\partial y}$$

所以梯度是一步一步传播的

如图是一个简单的神经网络用来举例：

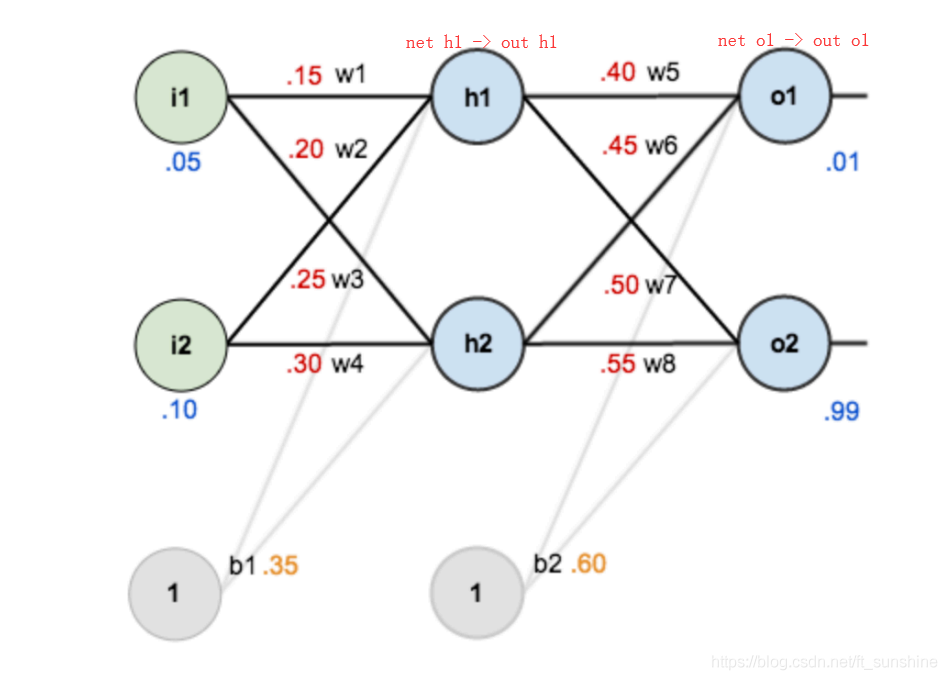
下面是前向（前馈）运算（激活函数为sigmoid）：

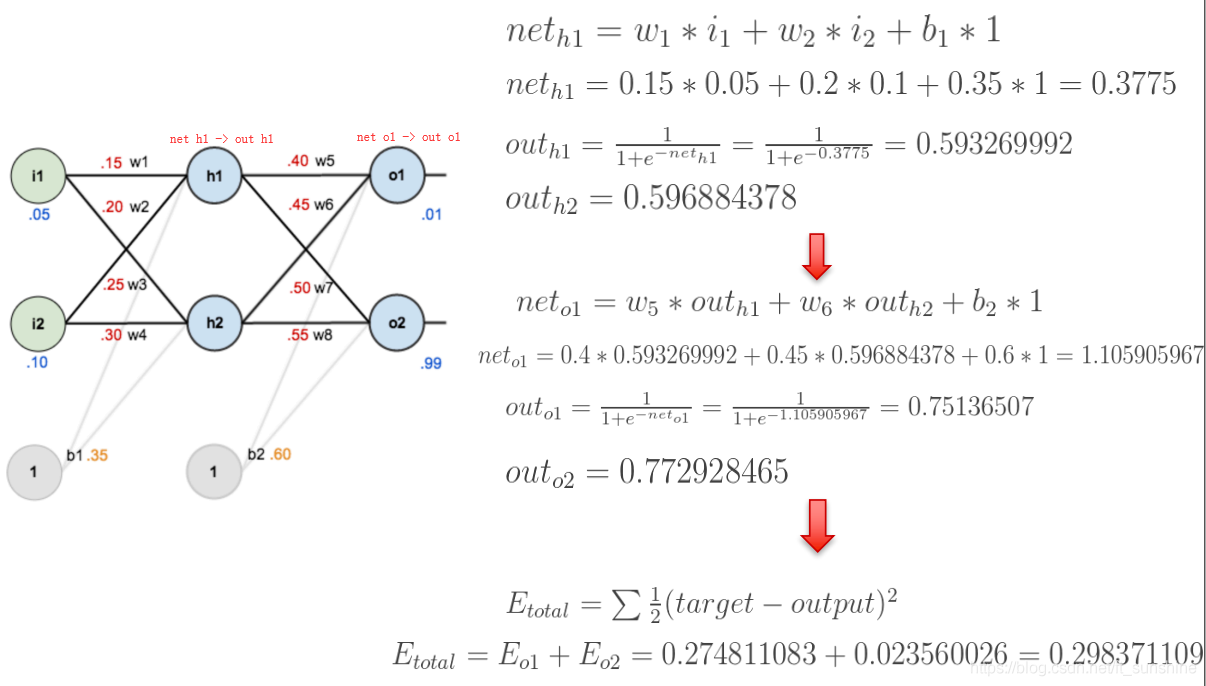
下面是反向传播（求网络误差对各个权重参数的梯度）：

我们先来求最简单的，求误差E对w5的导数。首先明确这是一个“链式求导”过程，要求误差E对w5的导数，需要先求误差E对out o1的导数，再求out o1对net o1的导数，最后再求net o1对w5的导数，经过这个链式法则，我们就可以求出误差E对w5的导数（偏导），如下图所示：

导数（梯度）已经计算出来了，下面就是反向传播与参数更新过程：

如果要想求误差E对w1的导数，误差E对w1的求导路径不止一条，这会稍微复杂一点，但换汤不换药，计算过程如下所示：

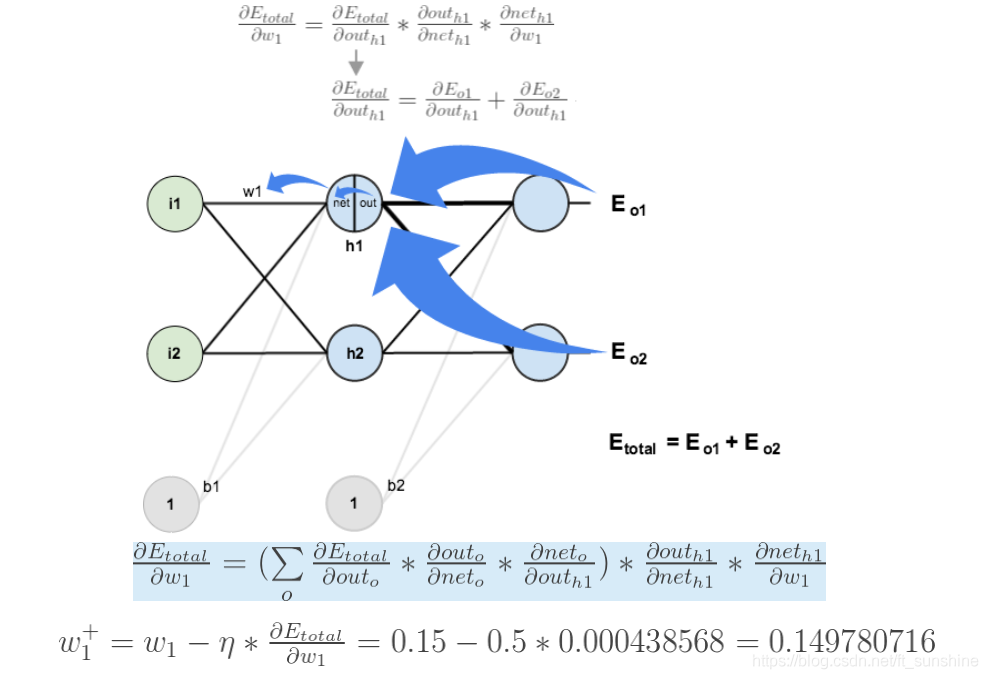
下面我们来看一下代码

# * 表示element-wise乘积，· 表示矩阵乘积

class Layer:
    '''中间层类'''
    self.W  # (input_dim, output_dim)
    self.b  # (1, output_dim)
    self.activate(a) = sigmoid(a)/tanh(a)/ReLU(a)/Softmax(a)

    def forward(self, input_data):       # input_data: (1, input_dim)
       '''单个样本的前向传播'''
       input_data · self.W + self.b = a  # a: (1, output_dim)
       h = self.activate(a)              # h: (1, output_dim)
       return h

    def backward(input_grad):
       '''单个样本的反向传播'''
       a_grad = input_grad * activate’(a)  # (1, output_dim)
       b_grad = a_grad                     # (1, output_dim)
       W_grad = (input_data.T) · a_grad    # (input_dim, output_dim)

       self.b -= learning_rate * b_grad 
       self.W -= learning_rate * W_grad

       return a_grad · (self.W).T          # (1, input_dim)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24