LeetCode-剑指68-II.二叉树的最近公共祖先

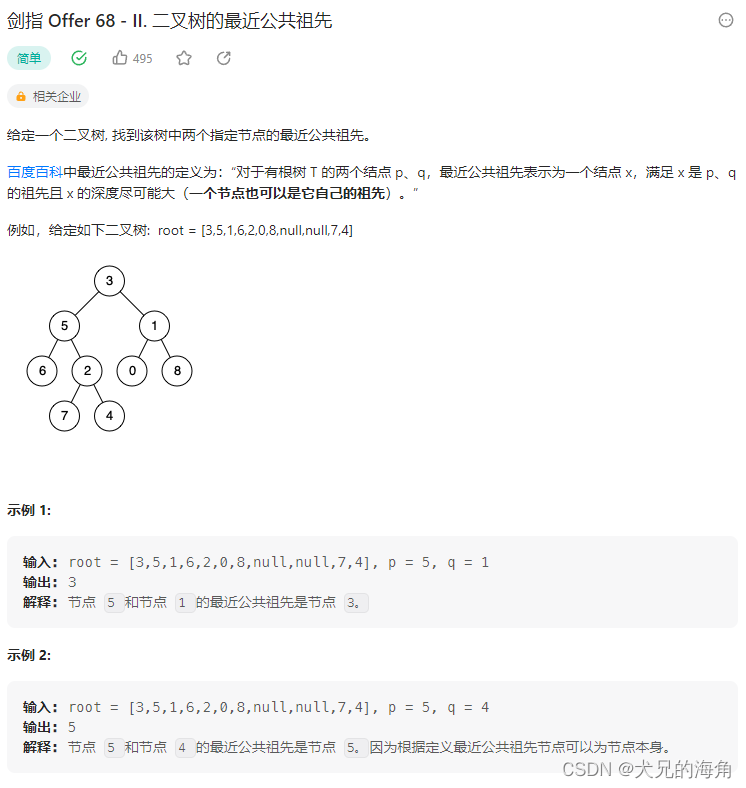
1、深度遍历

我们可以深度遍历每一个节点，若p或q落在当前节点的左右子树上或当前节点就是p或q节点返回true，否则返回false。我们深度遍历整棵二叉树，最终返回公共祖先。

class Solution {
public:
    TreeNode* ans;
    bool dfs(TreeNode* root, TreeNode* p, TreeNode* q) {
        if (root == nullptr) return false;
        bool lson = dfs(root->left, p, q);
        bool rson = dfs(root->right, p, q);
        if ((lson && rson) || ((root->val == p->val || root->val == q->val) && (lson || rson))) {
            ans = root;
        } 
        return lson || rson || (root->val == p->val || root->val == q->val);
    }
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        dfs(root, p, q);
        return ans;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

2、哈希表

我们可以遍历整棵二叉树，利用哈希表激励每个节点与其父节点之间的对应关系。而后我们首先从p节点开始向上遍历至节点为空，而后我们再向上遍历q节点，当新的q节点已经被访问过时，说明此时的节点就是p和q的公共祖先。

class Solution {
public:
    unordered_map<int, TreeNode*> fa;
    unordered_map<int, bool> vis;
    void dfs(TreeNode* root){
        if (root->left != nullptr) {
            fa[root->left->val] = root;
            dfs(root->left);
        }
        if (root->right != nullptr) {
            fa[root->right->val] = root;
            dfs(root->right);
        }
    }
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        fa[root->val] = nullptr;
        dfs(root);
        while (p != nullptr) {
            vis[p->val] = true;
            p = fa[p->val];
        }
        while (q != nullptr) {
            if (vis[q->val]) return q;
            q = fa[q->val];
        }
        return nullptr;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28