-
线性回归的梯度下降法——机器学习
一、实验内容
- 理解单变量线性回归问题;
- 理解最小二乘法;
- 理解并掌握梯度下降法的数学原理;
- 利用python对梯度下降法进行代码实现;
二、实验过程
1、算法思想
梯度下降法是一阶最优化算法。 要使用梯度下降法找到一个函数的局部极小值,必须向函数上当前点对应梯度(或者是近似梯度)的反方向的规定步长距离点进行迭代搜索。
最小二乘法,也叫做最小平方法,它通过最小化误差的平方和寻找数据的最佳函数匹配。利用最小二乘法可以简便地求得未知的数据,并使得这些求得的数据与实际数据之间误差的平方和为最小。最小二乘法还可用于曲线拟合。其他一些优化问题也可通过最小化能量或最小二乘法来表达。
2、算法原理
梯度下降法是迭代法的一种,可以用于求解最小二乘问题。在求解机器学习算法的模型参数,即无约束优化问题时,梯度下降法和最小二乘法是最常采用的方法。
在求解损失函数的最小值时,可以通过梯度下降法来迭代求解,得到最小化的损失函数和模型参数值。
3、算法分析
(1)确定当前位置的损失函数的梯度,对于,其梯度表达式为:
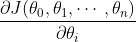
(2)用步长乘以损失函数的梯度,得到当前位置下降的距离,即。
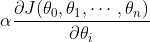
(3)确定是否所有的梯度下降的距离都小于,如果小于则算法终止,当前所有的
即为最终结果。否则进入第(4)步。
(4)更新所有的,更新表达式如下,更新完成后转入步骤(1):
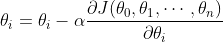
三、源程序代码
- import matplotlib.pyplot as plt
- import numpy as np
- from mpl_toolkits.mplot3d import Axes3D
- # 求fx的函数值
- def fx(x, y):
- return (x - 10) ** 2 + (y - 10) ** 2
- def gradient_descent():
- times = 100 # 迭代次数
- alpha = 0.05 # 学习率
- x = 20 # x的初始值
- y = 20 # y的初始值
- fig = Axes3D(plt.figure()) # 将画布设置为3D
- axis_x = np.linspace(0, 20, 100) # 设置X轴取值范围
- axis_y = np.linspace(0, 20, 100) # 设置Y轴取值范围
- axis_x, axis_y = np.meshgrid(axis_x, axis_y) # 将数据转化为网格数据
- z = fx(axis_x, axis_y) # 计算Z轴数值
- fig.set_xlabel('X', fontsize=14)
- fig.set_ylabel('Y', fontsize=14)
- fig.set_zlabel('Z', fontsize=14)
- fig.view_init(elev=60, azim=300) # 设置3D图的俯视角度,方便查看梯度下降曲线
- fig.plot_surface(axis_x, axis_y, z, rstride=1, cstride=1, cmap=plt.get_cmap('rainbow')) # 作出底图
- for i in range(times):
- x1 = x
- y1 = y
- f1 = fx(x, y)
- print("第%d次迭代:x=%f,y=%f,fxy=%f" % (i + 1, x, y, f1))
- x = x - alpha * 2 * (x - 10)
- y = y - alpha * 2 * (y - 10)
- f = fx(x, y)
- fig.plot([x1, x], [y1, y], [f1, f], 'ko', lw=2, ls='-')
- plt.show()
- if __name__ == "__main__":
- gradient_descent()
四、运行结果分析
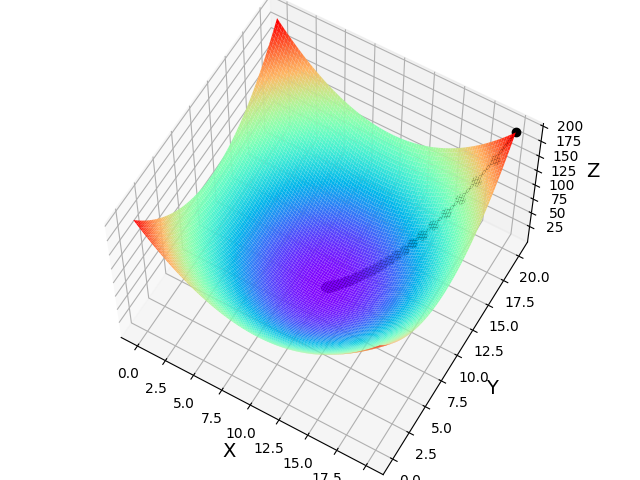
五、实验总结
线性回归求解可以使用最小二乘法和梯度下降法,下面我们针对两种方法进行对比:
相同点:本质和目标相同,两种都是经典的学习算法,在给定已知数据的情况下,利用求导算出一个模型(函数),使得损失函数最小,然后对给定的新数据进行估算预测。
不同点:
损失函数的选择:最小二乘法必须使用平方损失函数,而梯度下降可以选取其它函数;
实现方法不同,最小二乘法是实现全局最小,而梯度下降是一种迭代法;
一般最小二乘法一定可以得到全局最小,但对于多元计算繁琐,且复杂情况下未必有解。
而梯度下降的迭代比较简单,但找到的一般是局部最小,即极小值,仅在目标函数是下凸函数是才是全局最小,到最小点的收敛速度会变慢,且对初始点的选择极为敏感,而且步长的选择对损失函数也有影响。

-
相关阅读:
SpringCloud源码分析 (Eureka-Server-入口分析和处理Client状态请求) (五)
微服务和分布式的概念和区别
java多线程实现同步锁卖票窗口案例
AK 9.12 百度Java后端研发B卷 笔试
臻图信息ZTMapGIS系统助力智慧城市建设
cocos2d-x Android原生平台与Lua交互
01 【入门篇-介绍和安装】
3.16 - 传值与传址
机器学习的打分方程汇总
Configuring HSRP(Hot Standby Routing Protocol)
- 原文地址:https://blog.csdn.net/qq_50942093/article/details/128007034