-
48种数据分析可视化图表
可视化对于数据分析师来说可能不是最重要的,重要的是你分析或挖掘出来的结果是否有效。在这基础之上就需要通过可视化恰当完整的表达见解。这里又有区别了:实用性和美观性哪个更重要?要我说实用性是第一位的,能用一个元素表达最好不要用两个,能用一张图最好别用两张,尽可能用最简单的元素传达才能让你的观点最清晰。这就是数据科学领域经常会用到的“奥卡姆剃刀原理”。
有很多初学者可能搞不清数据分析可视化图表该怎么选择,这里介绍市面上使用占90%的图表以供大家作为参考,使用的时候可以来看看。同样,秉着MECE原则,不漏不重,尽可能全的囊括进来,然后再推荐常用的十种。
对于图表的分类,一直没有什么标准,每个可视化工具都不同,有的罗列,有的组合,有的分类。如果你百度如何选择图表,会看到一张作者为Andrew Abela的图表绘制指南图,里面根据比较、分布、联系、构成四类列举了21张图。它为很多人提供了指导,但是也存在一些问题:一是有些图表使用场景不合理,有些图工具画不出来;二是只有上面四种功能,还有趋势、聚类、异常的需求怎么用图表表达?
因此下面会通过这样一种介绍方式:
首先根据图表表达功能分为八大类48种列举,以窥全貌,知道图表能表达什么,哪些图表分别能表达什么;
其次从变量数量(也就是你有多少列数据)的角度,看你手中的数据能表达什么;
最后通过图形元素的角度,从点、线、 柱、大小、颜色、角度来看怎么搭配更准确、更美观表达数据。
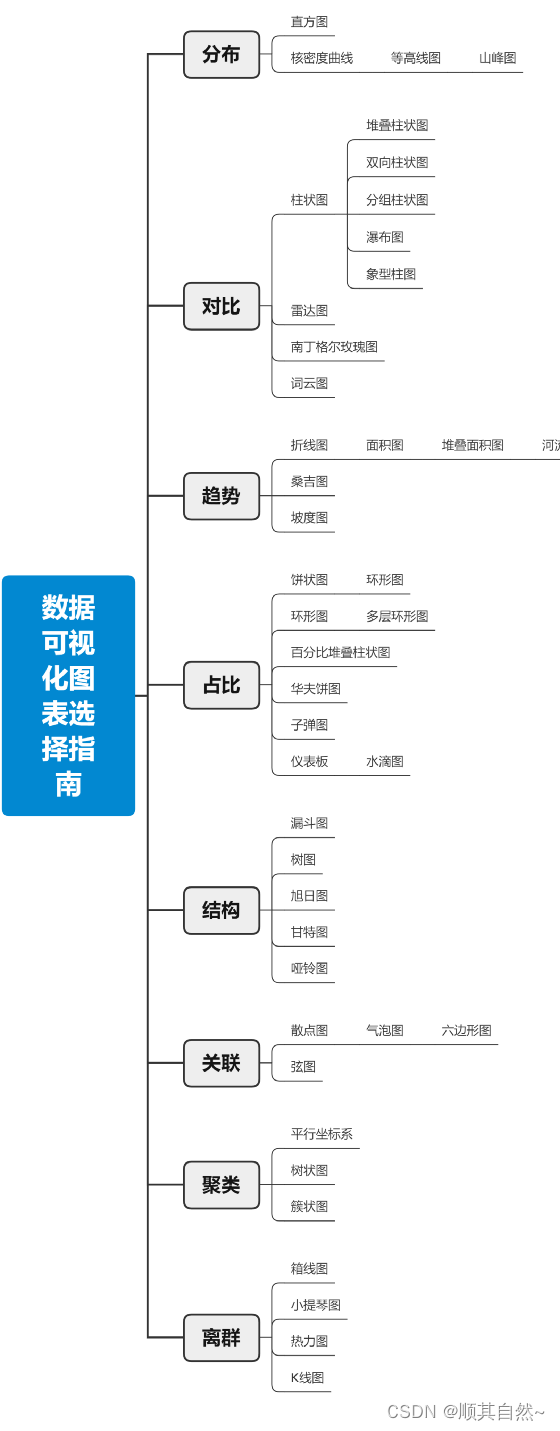
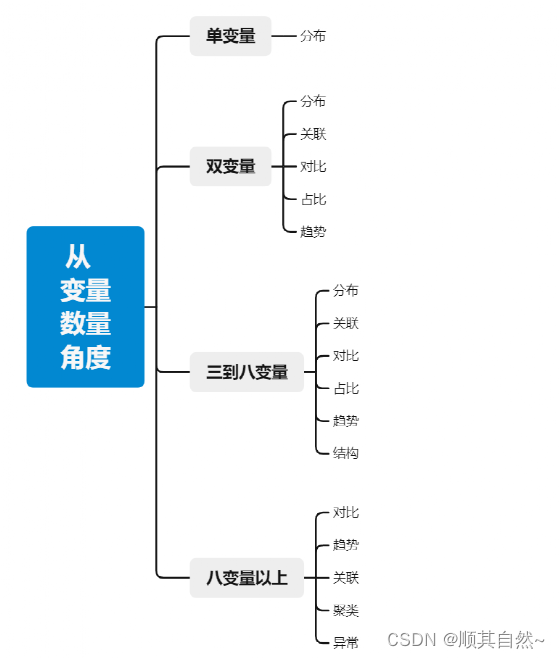
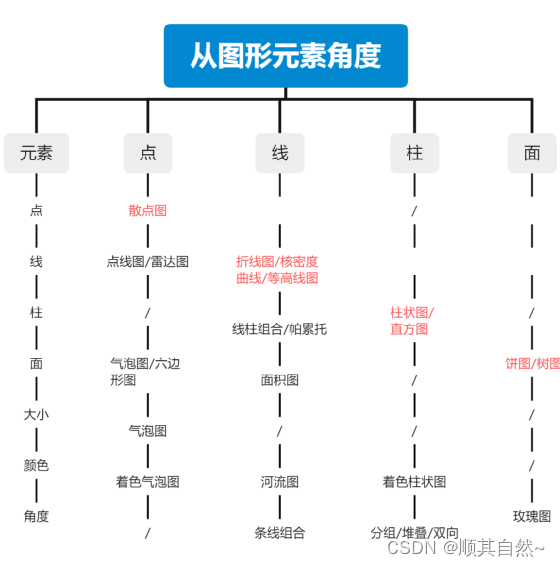
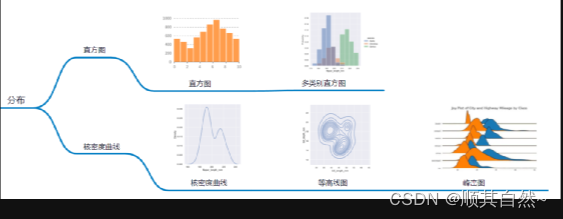
第一类、分布
1、直方图
统计图表,用于表示数据的分布情况。直方图与柱状图看似相像,实则完全不同。前者反映数据分布情况,后者则不具备此功能,只能对数值进行比较。从数据结构来说,柱状图需要1个分类变量,是离散的,柱子间有空隙。但直方图的数据均为连续的数值变量,因此柱子间是没有空隙的。直方图一般用于单个变量,如果是多个变量可以使用多变量直方图。
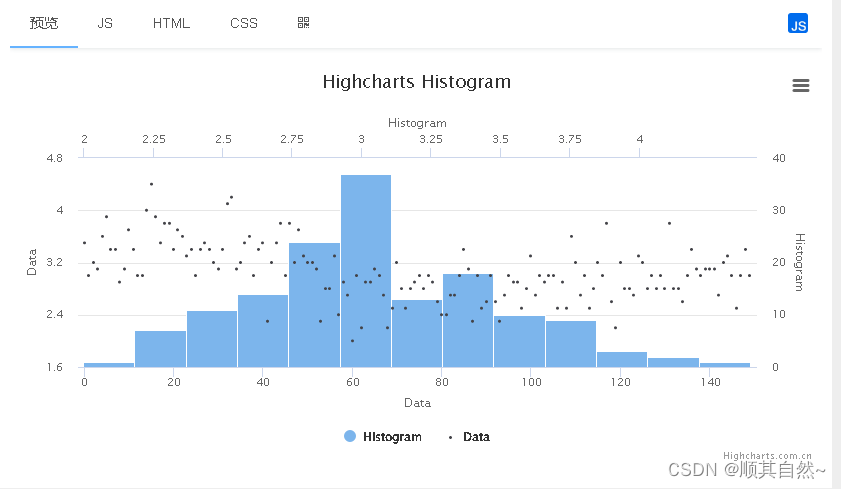
2、核密度曲线
统计图表,也是用于表示数据的分布情况。KDE图不是使用离散分箱,而是使用高斯核平滑产生连续密度估计。它也很像普通的曲线图,但是要记住它一条线是一个变量,曲线图是两个变量。如果要表达多个变量可以使用等高线图或者峰峦图(joyplot)。等高线图是二元变量,峰峦图是多元变量,但是变量数最好不要超过八个,图会很难看。
第二类、对比
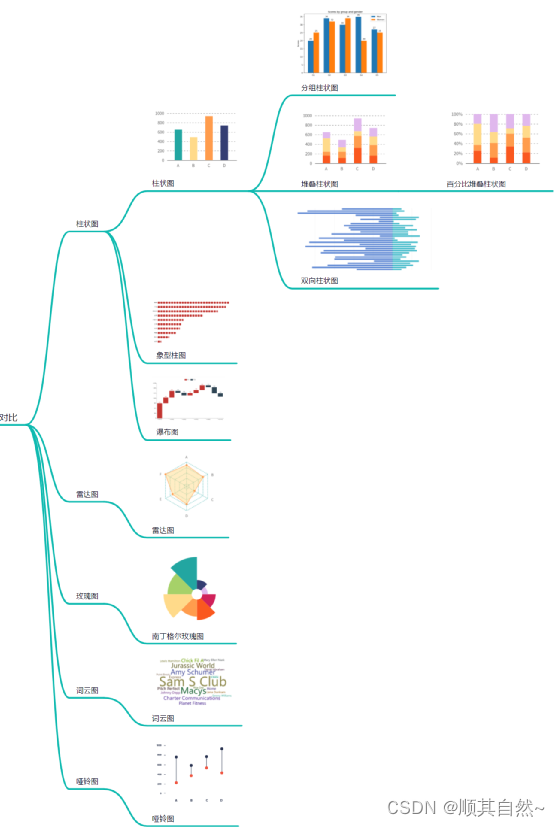
1、柱状图
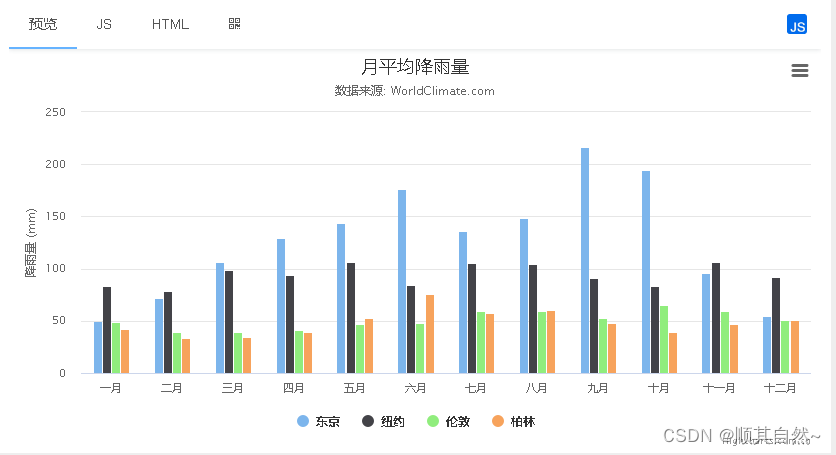
1.1、柱状图
普通图表,使用矩形条对不同类别进行数值比较的统计图表。这里把柱状图和条形图当一个类,只不过两者的柱子方向不同。它的核心功能是对比(当然如果分类变量是时间也可以具备发现趋势的功能)。最基础的柱形图,需要一个分类变量和一个数值变量。在柱状图上,分类变量的每个实体都被表示为一个矩形(通俗讲即为“柱子”),而数值则决定了柱子的高度。如果有分组,可以使用分组柱状图。
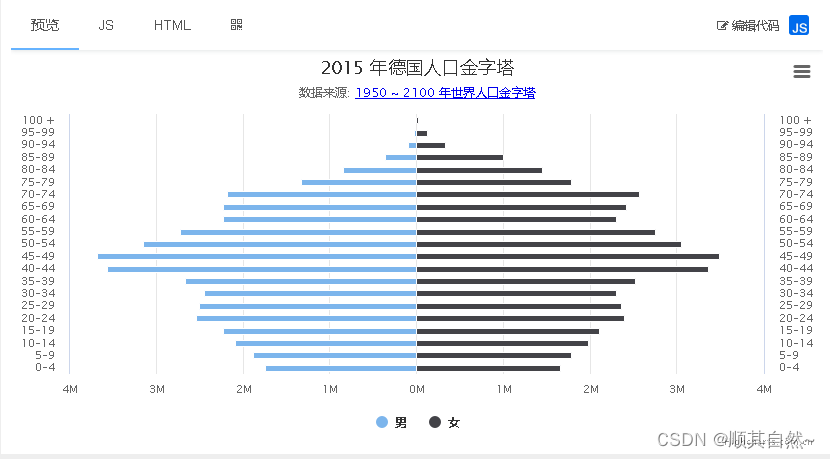
1.2、双向柱状图
又名正负条形图,使用正向和反向的柱子显示类别之间的数值比较。其中分类轴表示需要对比的分类维度,连续轴代表相应的数值,分为两种情况,一种是正向刻度值与反向刻度值完全对称,另一种是正向刻度值与反向刻度值反向对称,即互为相反数。
1.3、堆叠柱状图
常被用于比较不同类别的数值。而且,它的每一类数值内部,又被划分为多个子类别,这些子类别一般用不同的颜色来指代。如果说柱状图可以帮助我们观察“总量”,那么堆叠柱状图则可以同时反映“总量”与“结构”,即,总量是多少?它又是由哪些部分构成的?进而,我们还可以探究哪一部分比例最大,以及每一部分的变动情况,等等。

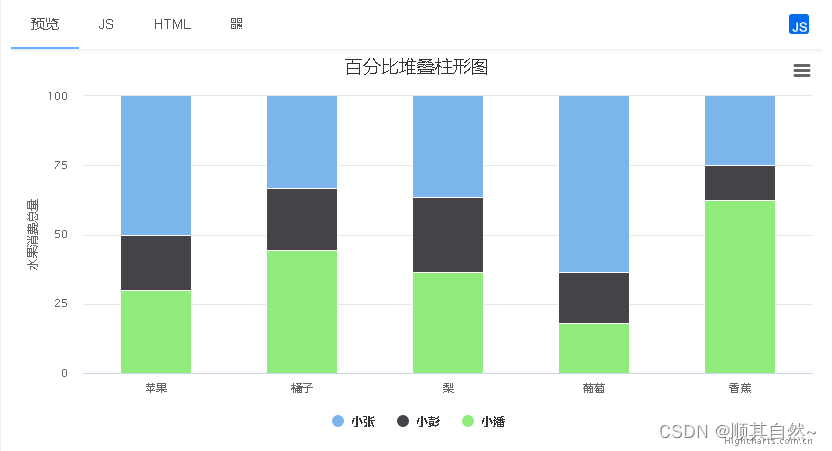
1.4、百分比堆叠柱状图
每根柱子是等长的,总额为100%。柱子内部被分割为多个部分,高度由该部分占总体的百分比决定。因此,与普通的柱状图或堆叠柱状图不同,100%堆叠柱状图不显示数据的“绝对数值”,而是显示“相对比例”。但同时,它也仍然具有柱状图的固有功能,即“比较”,我们可以通过比较多个柱子的构成,分析数值之间的相对差异,或者得出数值变化的趋势。
1.5、瀑布图
瀑布图( Waterfall Plot)采用绝对值与相对值结合的方式,适用于表达数个特定数值之间的数量变化关系。当想表达两个数据点之间数量的演变过程时,即可使用瀑布图。

2、雷达图
雷达图是一种显示多变量数据的图形方法。通常从同一中心点开始等角度间隔地射出三个以上的轴,每个轴代表一个定量变量,各轴上的点依次连接成线或几何图形。雷达图可以用来在变量间进行对比,或者查看变量中有没有异常值。另外,多幅雷达图之间或者雷达图的多层数据线之间,还可以进行总体数值情况的对比。轴的相对位置和角度通常是无信息的。每个变量都具有自己的轴,彼此间的距离相等,所有轴都有相同的刻度。在将数据映射到这些轴上时,需要注意预先对数值进行标准化处理,保证各个轴之间的数值比例能够做同级别的比较。
3、南丁格尔玫瑰图
又名鸡冠花图、极坐标区域图。尽管外形很像饼图,但本质上来说,南丁格尔玫瑰图更像在极坐标下绘制的柱状图。只不过,它用半径来反映数值(而饼图是以扇形的弧度来表示数据的)。但是,由于半径和面积之间是平方的关系,视觉上,南丁格尔玫瑰图会将数据的比例夸大。
4、词云图
通过形成“关键词云层”或“关键词渲染”,对网络文本中出现频率较高的“关键词”的视觉上的突出。
5、哑铃图
指用一条横线连接两个点、看起来有点像哑铃的图,适用于强调从一个点到另一个点的变化。
第三类、趋势

1、折线图
统计图表,常用来表示数值随连续时间间隔或有序类别的变化。在折线图中,x轴通常用作连续时间间隔或有序类别,y轴用于量化的数据,如果为负值则绘制于y轴下方。连线用于连接两个相邻的数据点。折线图用于分析事物随时间或有序类别而变化的趋势。如果有多组数据,则用于分析多组数据随时间变化或有序类别的相互作用和影响。折线的方向表示正/负变化。折线的斜率表示变化的程度。从数据上来说,折线图需要一个连续时间字段或一个分类字段和至少一个连续数据字段。
2、面积图
普通图表,或称区域图,是一种随有序变量的变化,反映数值变化的统计图表,原理与折线图相似,它的特点在于,折线与自变量坐标轴之间的区域,会由颜色或者纹理填充。也可用于多个系列数据的比较。这时,面积图的外观看上去类似层叠的山脉,在错落有致的外形下表达数据的总量和趋势。不仅可以清晰地反映出数据的趋势变化,也能够强调不同类别的数据间的差距对比。
3、桑基图 (Sankey Diagram)
是一种表现流程的示意图,用于描述一组值到另一组值的流向。分支的宽度对应了数据流量的大小。有时也被称为“冲积图”(Alluvial diagram)。这种图包含流入、流出的节点,以及曲线型的边,往往呈现出彩带一般的效果。其一大特点在于“能量守恒”,即起始流量和结束流量相同。不能在中间过程中创造出流量,流失的流量也不应莫名消失(可以流向表示损耗的节点)。也因为流出等于流入,桑基图的每条边,宽度应是保持不变的。使用桑基图时,应注意变量的归类和颜色的选择,避免太过花哨、影响阅读。必要时建议加入交互功能。
4、坡度图
跟折线图很像,但是只有两个点,而折线图适用于多个,适合比较给定项目的“前”和“后”位置和趋势。
第四类、占比
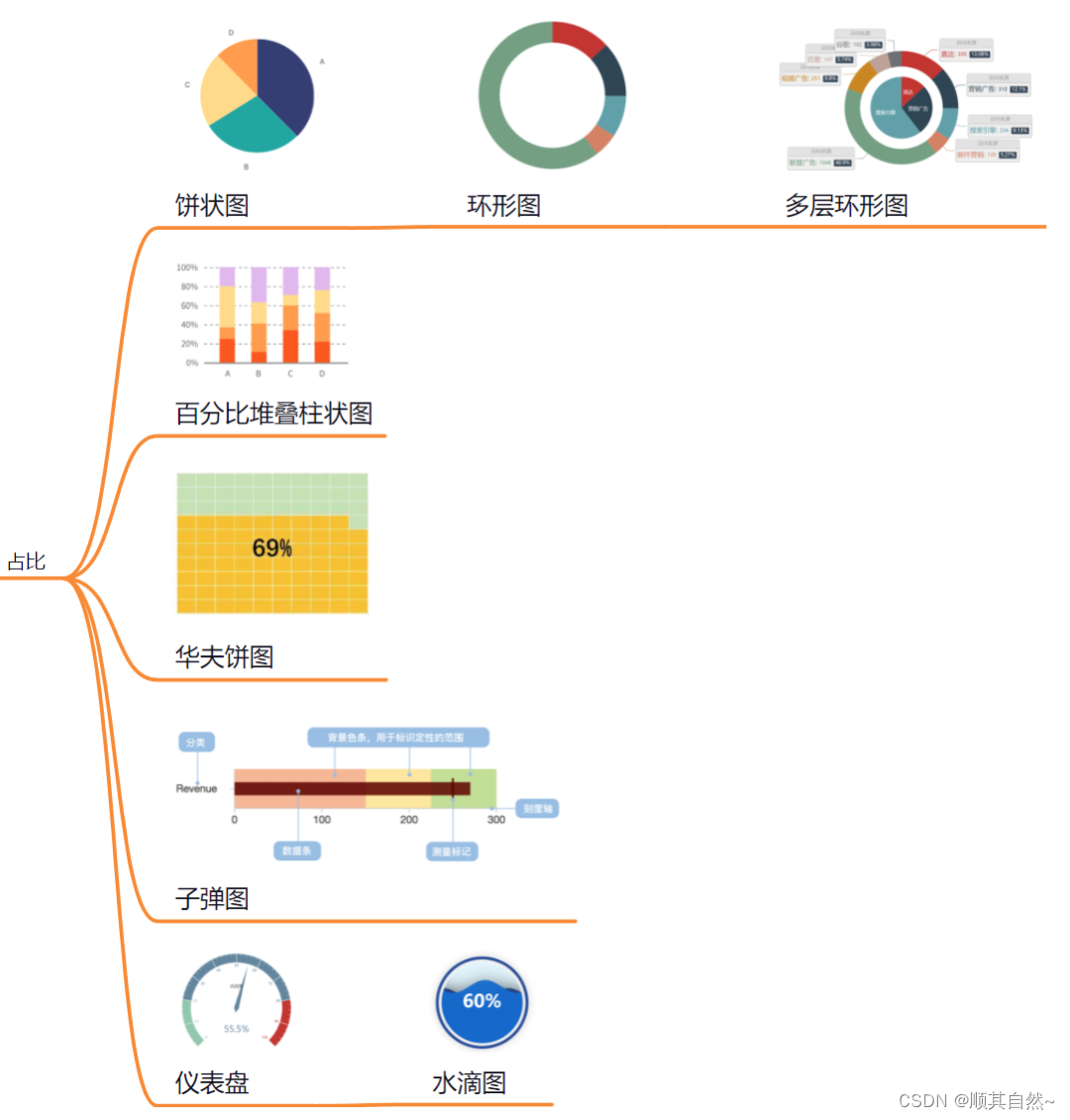
1、饼状图
统计图表,划分为几个扇形的圆形统计图表。饼图最显著的功能在于表现“占比”。从数据来看,饼图一般需要一个分类数据字段、一个连续数据字段。值得注意的是,分类字段的数据,在图表使用的语境下,应当构成一个整体而不能是独立、无关的。使用时,须确认各个扇形的数据加起来等于100%;避免扇区超过5个,尽量让图表简洁明了;注意扇形的排布顺序,一般情况下,将最大的扇形放在12点钟方向,接下来按面积依次排列;最后,正确使用颜色,既区分出需要强调的扇形,又不致于让人眼花缭乱。
2、华夫饼图(Waffle Chart)
又称为直角饼图,可以直观的描绘百分比完成比例情况。与传统的饼图相比较,华夫饼图表达的百分比更清晰和准确,它的每一个格子代表 1%。华夫饼图的典型应用是比较同类型指标完成比例。
3、子弹图
子弹图的发明是为了取代仪表盘上常见的那种里程表,时速表等基于圆形的信息表达方式。每一个单元的子弹图只能显示单一的数据信息源;通过添加合理的度量标尺可以显示更精确的阶段性数据信息;通过优化设计还能够用于表达多项同类数据的对比;可以表达一项数据与不同目标的校对结果。
4、仪表盘
直观的表现出某个指标的进度或占比情况。
第五类、结构
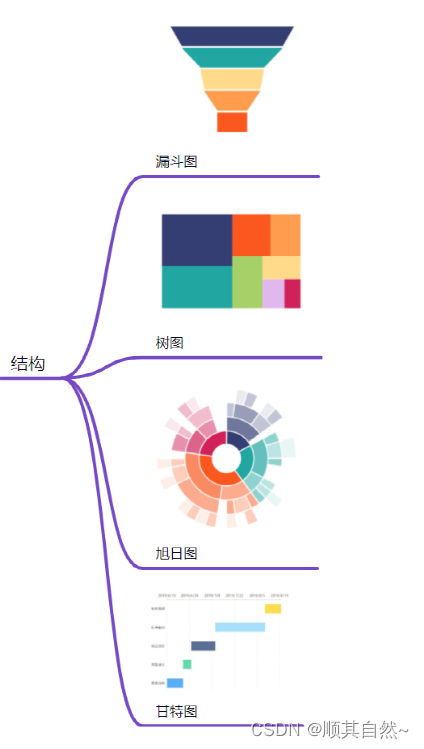
1、漏斗图
普通图表,形如“漏斗”,用于单流程分析,在开始和结束之间由N个流程环节组成。漏斗图的起始总是100%,并在各个环节依次减少,每个环节用一个梯形来表示,整体形如漏斗。漏斗图的各个环节,有逻辑上的顺序关系。同时,漏斗图的所有环节的流量都应该使用同一个度量。漏斗图最适宜用来呈现业务流程的推进情况,如用户的转化情况。通过漏斗图,可以较直观的看出流程中各部分的占比、发现流程中的问题,进而做出决策。
2、树图
统计图表,又叫矩形树图,是一个由不同大小的嵌套式矩形来显示树状结构数据。在矩形树图中,父子层级由矩形的嵌套表示。在同一层级中,所有矩形依次无间隙排布,他们的面积之和代表了整体的大小。单个矩形面积由其在同一层级的占比决定。
3、旭日图
普通图表,是一种表现层级数据的图表。它以父子层次结构来显示数据,并构成一个同心圆,因此又被成为称为多层饼图。离原点越近,数据的层级越高。换句话说,相邻的两层,内层是外层的“父”。同时,一个“父”可以有多个“子”,即某一个环形又可以被分割成多个环形。旭日图的本质是树状关系,与树图等价的,因此也被称为极坐标下的矩形树图。它可以在承载大量数据的同时,清晰的显示数据间的结构关系。
4、甘特图
普通图表,又称为横道图、条状图(Bar chart)。其通过条状图来显示项目、进度和其他时间相关的系统进展的内在关系随着时间进展的情况。
第六类、关联
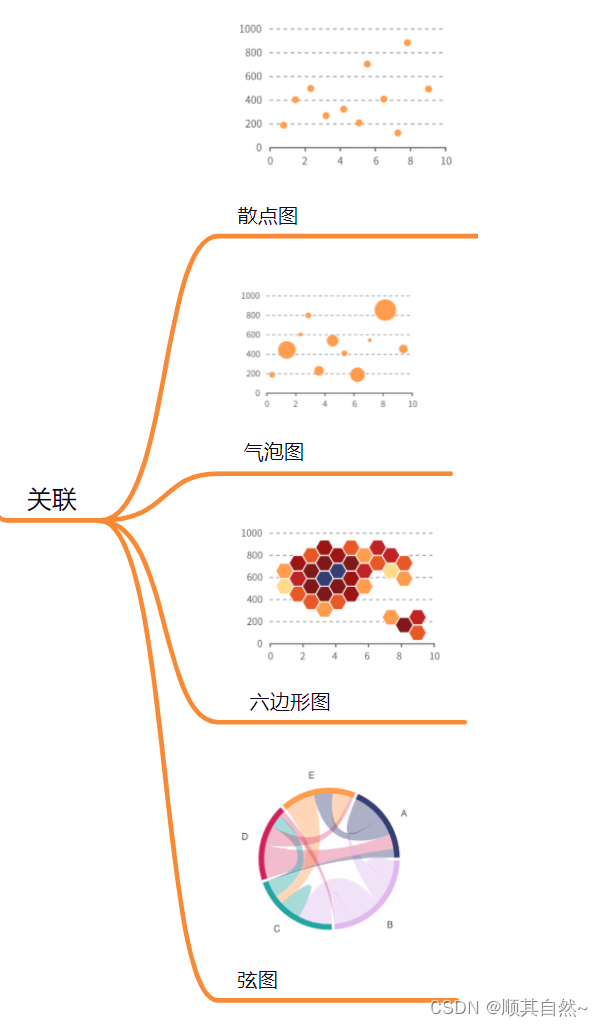
1、散点图
统计图表,将所有的数据以点的形式展现在平面直角坐标系上。它至少需要两个不同变量,一个沿x轴绘制,另一个沿y轴绘制。每个点在X、Y轴上都有一个确定的位置。众多的散点叠加后,有助于展示数据集的“整体景观”,从而帮助我们分析两个变量之间的相关性,或找出趋势和规律。
1)如果两个变量的散点看上去都在一条直线附近波动,则称变量之间是线性相关的;
2)如果散点图呈现出一个集中的大致趋势,这种趋势通常可以用一条光滑的曲线来近似,这样近似的过程被称为曲线拟合,而这条曲线则被称为最佳拟合线或趋势线。
3)如果图中存在个别远离集中区域的数据点,这样的点被称为离群点或异常值。
2、气泡图
普通图表,可以看作是散点图的变形。在气泡图中,一般情况下,每一个气泡都代表着一组三个维度的数据。其中两个决定了气泡在笛卡尔坐标系中的位置(即x,y轴上的值),另外一个则通过气泡的大小来表示。气泡图通常用于展示和比较数据之间的关系和分布,通过比较气泡位置和大小来分析数据维度之间的相关性。也可以用作研究两个变量与时间变量的关系。如果再多一维变量,还可以使用颜色区分。
3、六边形分箱图(Hexagonal Binning)
普通图表,也称六边形图,既是散点图的延伸,又兼直方图和热力图的特征。散点图常来分析变量之间的关系,以及寻找趋势。但是随着数据集越来越庞大,画面上的散点也越来越多。这时,数据点很可能会重叠在一起、互相覆盖,以至于很难分辨出趋势、发现集群。借鉴热力图,用颜色代表频数的高低。
4、弦图
普通图表,是一种表示实体之间相互关系的图形方法。由节点分段和弧形的边构成。节点分段沿圆周排列,节点之间的关系通过使用弧线相互连接,这些弧线是有宽度的,且起止宽度可以不一样,弧线的宽度反映了一种矩阵关系。它可以在“多类别+复杂关系”的情况下,有效降低视觉复杂度。就场景而言,弦图最常被用来表现复杂的关系、以及数据的流动情况等。
第七类、聚类
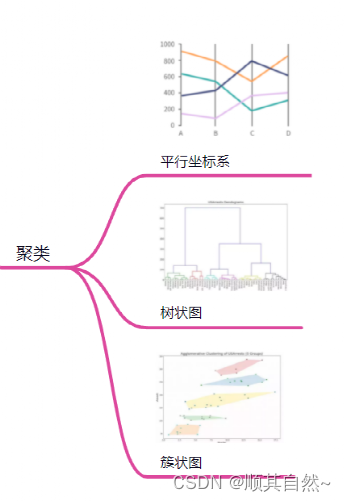
1、平行坐标图
统计图表,含有多个垂直平行坐标轴图表。每个垂直坐标轴表示一个字段,每个字段又用刻度来标明范围。这样,一个多维的数据可以很容易的在每一条轴上找到“落点”,从而连接起来,形成一条折线。随着数据增多,折线堆叠,分析者则有可能从中发现特性和规律,比如发现数据之间的聚类关系。
2、树状图
跟树图表示占比的含义完全不同,这里是聚类图形。相同的子树在一个分支下,直观的显示聚类关系和层次关系。
3、簇状图
可用于划分属于同一群集的点,用SPSS画。
第八类、离群
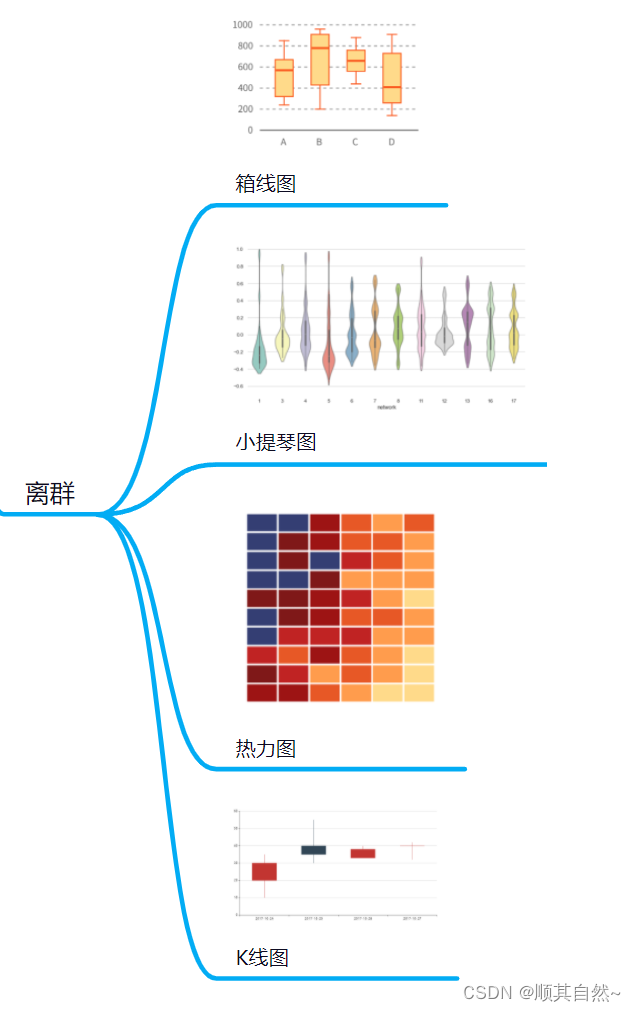
1、箱形图
统计图表,一种用作显示一组数据分布情况,它能显示出一组数据的最大值、最小值、中位数及上下四分位数。从箱子延伸出去的线条展现出了上下四分位数以外的数据,这代表离群值,也可称之为异常值。框的不同部分之间的间距表示数据中的分散程度(扩散)和偏斜,并显示离群值。
2、小提琴图
和箱线图有点儿类似,用来显示数据分布和概率密度。这种图结合了箱线图和密度图的特征,用来显示数据的分布形状。它可以很直观的显示离群值的位置。
3、热力图
统计图表,通过对色块着色来显示数据。绘图时,需指定颜色映射的规则。例如,较大的值由较深的颜色表示,较小的值由较浅的颜色表示;较大的值由偏暖的颜色表示,较小的值由较冷的颜色表示。热力图适合用于查看总体的情况、发现异常值、显示多个变量之间的差异,以及检测它们之间是否存在任何相关性。
4、K线图
普通图表,适合的数据,一个时间数据字段,五个连续字段。多个放在一起可以观察数据的变化、对比和趋势分类数值大小。单个可以用做箱型图,来观察离群值。
以上就是数据分析师90%都会用到的图表啦,所用示例图表都来自于pyecharts/seaborn/AntV,以及图之典这个网站,强烈推荐大家收藏图之典,对图表使用有详细的用法介绍。
这里要说的是有四类图没有列举:一是维恩图、同心圆图,这类是信息图,不是数据分析图;二是地图,以地图为底可以叠加散点图、折线图、柱状图什么的,但是主要以地理分析为主,专业性比较强;三是网状图、星形图;四是用极坐标来画的图(除了玫瑰图,直角坐标画的图很多都可以用极坐标画)。
图表选择的原则见仁见智,我在上面就提供了一种,比较实用好上手。看起来多,实际上最最常用的不超过20种,如果还不会选,那就老老实实直方图、散点图、折线图、饼图、柱状图、树图、面积图、、雷达图、气泡图、仪表盘这十种吧,可以说基本把八种图表表达功能给囊括了。每一个图表核心可能是表达一个功能,但如果与其他元素结合也可以具备多个功能。比如柱状图最核心是对比/比较,但是如果与时间相结合呢?就有趋势的功能;如果堆叠起来呢?就有了占比的功能。环形图单个表示占比,两个表示对比,与时间结合就可能表示趋势了。所以在选择图表时,尽可能理解每个图表的元素和可表达可视化作用,这样就能做出兼具实用性和美观性的图表啦。
-
相关阅读:
【Django】执行查询—创建和修改对象
武汉新时标文化传媒有限公司“土味”正在崛起,短视频的春天来了
2. Go中的常用命令
数据结构——栈&队列
Linux上x86_64架构的动态链接器 ld-linux-x86-64.so.2
用飞书写博客,并自动部署
《Python魔法大冒险》005 魔法挑战:自我介绍机器人
三道动态规划题-最长的有效括号、组合总和I、组合总和II
java-php-python-springboot校园实习管理系统计算机毕业设计
三、考研C语言笔记——C语言的组成,数据,数据类型的区别,常量与变量区别,表达式中考点
- 原文地址:https://blog.csdn.net/fuhanghang/article/details/128016831