【math】利用Cardano方法对一元三次方程求解及python实现

【参考】

• 用Cardano方法求解三次方程介绍
• cardano方法求解
• 下载cardano方法包
• x^3+1=0求解问题、三次方程反函数问题
• Micorsoft-Math-solver 微软数学工具
• WolframAlpha: inverse of a function/反函数
• 百度百科-一元三次方程求根公式

【问题描述】

求解一元三次方程

求解一元三次方程：
$$a{x}^3+b{x}^2+cx+d=0$$

求解有多种方法，其中Cardano方法得到的解为：

一元三次多项式：$y=f(x)=a{x}^3+b{x}^2+cx+d$ => $a{x}^3+b{x}^2+cx+d-y=0$

【代码实现】

现成的包 cardano_method

• 可以使用python包：安装cardano_method 【参考这里】

  pip install cardano_method
  1

  该包的使用：CubicEquation函数对应第一个参数列表是：[a, b, c, d]，即求解方程的各系数。

  from cardano_method.cubic import CubicEquation
  a = CubicEquation([1, 3, 4, 4])
  print(a.answers)  # j表示虚部后缀
  # [(-2+0j), (-0.5+1.322875j), (-0.5-1.322875j)]
  print(a.answers[0].real)  # 获取第一个解的实部
  print(a.answers[0].imag)  # 获取第一个解的虚部
  1
  2
  3
  4
  5
  6

  但是发现一个问题：解方程$x^3+1=0$时，居然报错分母是0：ZeroDivisionError。

  a = CubicEquation([1, 0, 0, 1])
  1

  
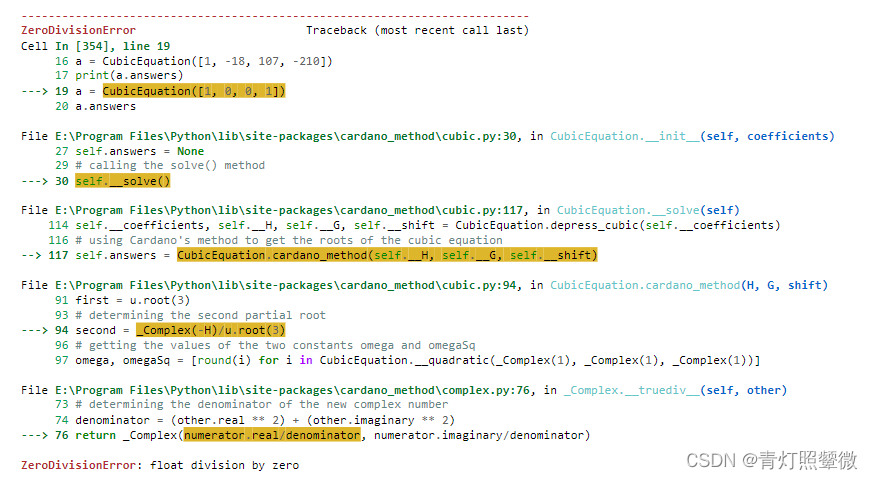
  但实际上，$x^3+1=0$的解是对应：$x_1=-1$, $x_2=\frac{1}{2}+\frac{\sqrt{3}}{2}i$, $x_3=\frac{1}{2}-\frac{\sqrt{3}}{2}i$（这里$i$表示虚数）。需要详细看下包中bug如何解决？

根据公式编写求解代码

1. 可以根据对应解的公式写出求解函数：【注意：关于浮点型计算有问题？】

   def cardano_solution_v0(a, b, c, d):
       ab = -b/float(3*a)
       q = (3*a*c-(b**2)) / (9*(a**2))
       r = (9*a*b*c-27*(a**2)*d-2*(b**3)) / (54*(a**3))
       delta_sqrt = (q**3+r**2)**(1.0/2)
       
       s = (r+delta_sqrt)**(1.0/3)
       t = (r-delta_sqrt)**(1.0/3)
       imag = complex(0, (s-t)*(3**(1.0/3))/2)
       x1 = s+t+ab
       x2 = -(s+t)/2+ab+imag
       x3 = -(s+t)/2+ab-imag
       return x1, x2, x3
   1
   2
   3
   4
   5
   6
   7
   8
   9
   10
   11
   12
   13

   测试修改保留浮点，还是有问题，跟cardano_method包的结果对不上？？？【注：cardano_solution_v0和cardano_solution_v1都有问题，正确的解见下方函数：cardano_solution】

   def round_ri(xo, n=4):
       xr, xi = round(xo.real, n), round(xo.imag, n)
       if xi == 0:
           return xr
       else:
           return complex(xr, xi)
   
   def cardano_solution_v1(a, b, c, d):
       ab = -b/float(3*a)
       q = (3*a*c-(b**2)) / (9*(a**2))
       r = (9*a*b*c-27*(a**2)*d-2*(b**3)) / (54*(a**3))
       delta_sqrt = round((q**3+r**2)**(1.0/2), 4)
       
       # print("r, delta_sqrt:", r, delta_sqrt, round(r-delta_sqrt, 4))
       s = round((r+delta_sqrt)**(1.0/3), 8)
       t = round(r-delta_sqrt, 4)**(1.0/3)
       print("st,ab:", s, t, ab)
       imag = complex(0, (s-t)*(3**(1.0/3))/2)
       x1 = s+t+ab
       x2 = -(s+t)/2+ab+imag
       x3 = -(s+t)/2+ab-imag
       return round_ri(x1), round_ri(x2), round_ri(x3)
   1
   2
   3
   4
   5
   6
   7
   8
   9
   10
   11
   12
   13
   14
   15
   16
   17
   18
   19
   20
   21
   22

   是公式本身写的有误？还是浮点/开根号问题？需要再检查。。。

2. 测试其他公式： 百度百科-一元三次方程求根公式

   这里是说，一元三次方程的系数是复数时，用Cardano公式有问题（什么问题？），旧使用如下通用的求根公式：
   

   def cardano_solution(a, b, c, d):
       #u = round((9*a*b*c-27*(a**2)*d-2*(b**3)) / (54*(a**3)), 4)
       #v = round(3*(4*a*c**3 - b**2*c**2-18*a*b*c*d+27*a**2*d**2+4*b**3*d) / (18**2*a**4), 4) ** (1.0/2)
       u = (9*a*b*c-27*(a**2)*d-2*(b**3)) / (54*(a**3))
       v = (3*(4*a*c**3 - b**2*c**2-18*a*b*c*d+27*a**2*d**2+4*b**3*d) / (18**2*a**4)) ** (1.0/2)
       if abs(u+v) >= abs(u-v):
           m = (u+v) ** (1.0/3)
       else:
           m = (u-v) ** (1.0/3)
       if m == 0: 
           n == 0
       else:
           n = (b**2-3*a*c) / (9*a**2*m)
       # w = complex(0, -0.5+(3/4)**(1.0/2))
       # w2 = complex(0, -0.5-(3/4)**(1.0/2))
       w = -0.5+(-3/4)**(1.0/2)
       w2 = -0.5-(-3/4)**(1.0/2)
       ab = -b/float(3*a)
       x1 = m+n+ab
       x2 = w*m+w2*n+ab
       x3 = w2*m+w*n+ab
       # return x1, x2, x3
       return round_ri(x1), round_ri(x2), round_ri(x3)
   1
   2
   3
   4
   5
   6
   7
   8
   9
   10
   11
   12
   13
   14
   15
   16
   17
   18
   19
   20
   21
   22
   23

   测试结果cardano_solution和cardano_method包可以对上，且求解 $x^3+1=0$ 没有问题：

   print(cardano_solution(1,3,4,4))
   print(cardano_solution(1,0,0,-1))
   print(cardano_solution(1,0,0,1))
   # ((-0.5+1.3229j), -2.0, (-0.5-1.3229j))
   # (1.0, (-0.5+0.866j), (-0.5-0.866j))
   # ((0.5+0.866j), -1.0, (0.5-0.866j))
   
   print(CubicEquation([1,3,4,4]).answers)
   print(CubicEquation([1,0,0,-1]).answers)
   print(CubicEquation([1,0,0,1]).answers)  # 报错
   # [(-2+0j), (-0.5+1.322875j), (-0.5-1.322875j)]
   # [(1+0j), (-0.5+0.866025j), (-0.5-0.866025j)]
   # ZeroDivisionError ...
   1
   2
   3
   4
   5
   6
   7
   8
   9
   10
   11
   12
   13

【总结】

• 根据公式自己编写的函数cardano_solution可求解一元三次方程。
• 下载的包cardano_method和直接使用Cardano公式写的函数有问题。原因是？

---

附： python 获取复数的实部和虚部。使用j后缀表示虚数，比如a+bj中，a是实部，b是虚部，python中用complex(a,b)生成一个复数。

x = 2+1.5j
print(x.real)  # 打印实部：2
print(x.imag)  # 打印虚部：2
x1 = complex(2,1.5)  # 使用`complex`生成复数 2+1.5j
1
2
3
4