区间信息维护与查询【最近公共祖先LCA 】 - 原理

区间信息维护与查询【最近公共祖先LCA 】 - 原理

最近公共祖先（Lowest Common Ancestors，LCA）指有根树中距离两个节点最近的公共祖先。

祖先指从当前节点到树根路径上的所有节点。

u 和v 的公共祖先指一个节点既是u 的祖先，又是v 的祖先。u 和v 的最近公共祖先指距离u 和v 最近的公共祖先。若v 是u 的祖先，则u 和v 的最近公共祖先是v 。

可以使用LCA求解树上任意两点之间的距离。求u 和v 之间的距离时，若u 和v 的最近公共祖先为lca，则u 和v 之间的距离为u 到树根的距离加上v 到树根的距离减去2倍的lca到树根的距离：dist[u]+dist[v ]-2×dist[lca]。

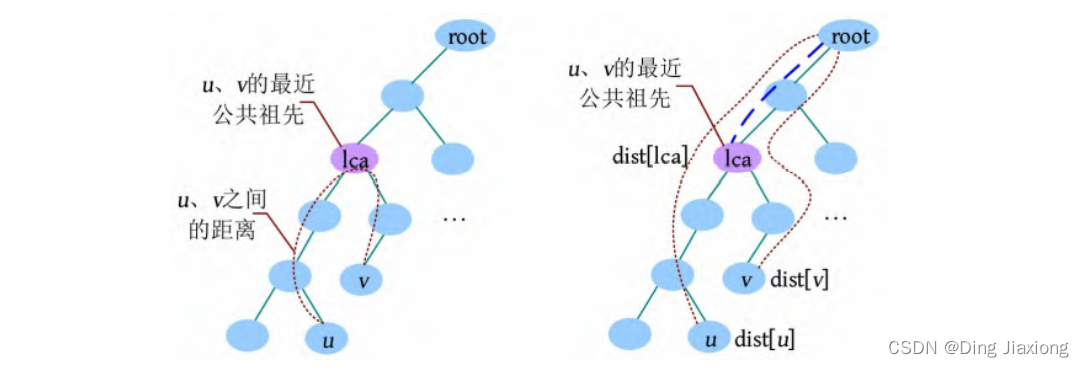
求解LCA的方法有很多，包括暴力搜索法、树上倍增法、在线RMQ算法、离线Tarjan算法和树链剖分。

• 在线算法： 以序列化方式一个一个地处理输入，也就是说，在开始时并不需要知道所有输入，在解决一个问题后立即输出结果。
• 离线算法： 在开始时已知问题的所有输入数据，可以一次性回答所有问题。

【原理1】 暴力搜索法

暴力搜索法有两种：向上标记法和同步前进法。

① 向上标记法

从u 向上一直到根节点，标记所有经过的节点；若v 已被标记，则v 节点为LCA(u , v )；否则v 也向上走，第1次遇到已标记的节点时，该节点为LCA(u , v )。

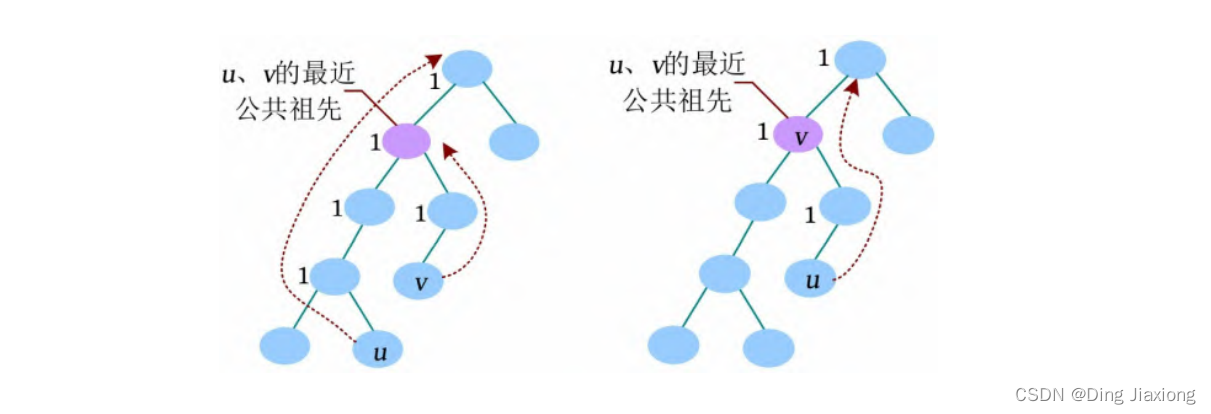
② 同步前进法

将u、v 中较深的节点向上走到和深度较浅的节点同一深度，然后两个点一起向上走，直到走到同一个节点，该节点就是u、v 的最近公共祖先，记作LCA(u , v )。若较深的节点u 到达v 的同一深度时，那个节点正好是v ，则v 节点为LCA(u , v )。

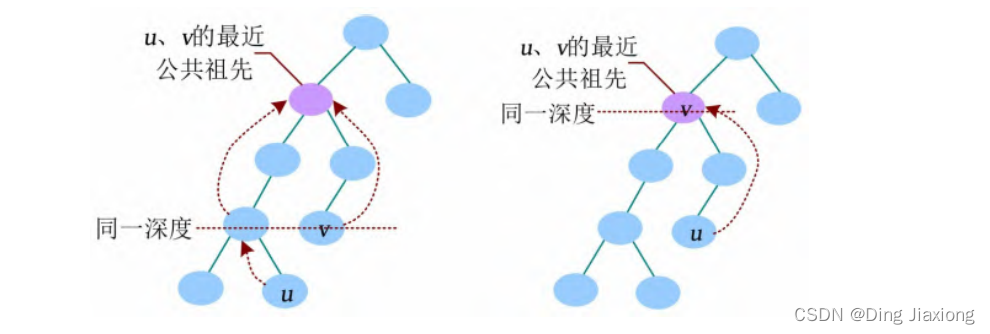
③ 算法分析

以暴力搜索法求解LCA，两种方法的时间复杂度在最坏情况下均为O(n )。

【原理2】 树上倍增法

树上倍增法不仅可以解决LCA问题，还可以解决很多其他问题，掌握树上倍增法是很有必要的。

F[i , j ]表示i 的2j 辈祖先，即i 节点向根节点走2 j 步到达的节点。

u 节点向上走20 步，则为u 的父节点x ，F[u , 0]=x ；向上走2^1步，到达y ，F[u , 1]=y ；向上走2^2 步，到达z ，F[u , 2]=z ；向上走2^3 步，节点不存在，令F[u , 3]=0。

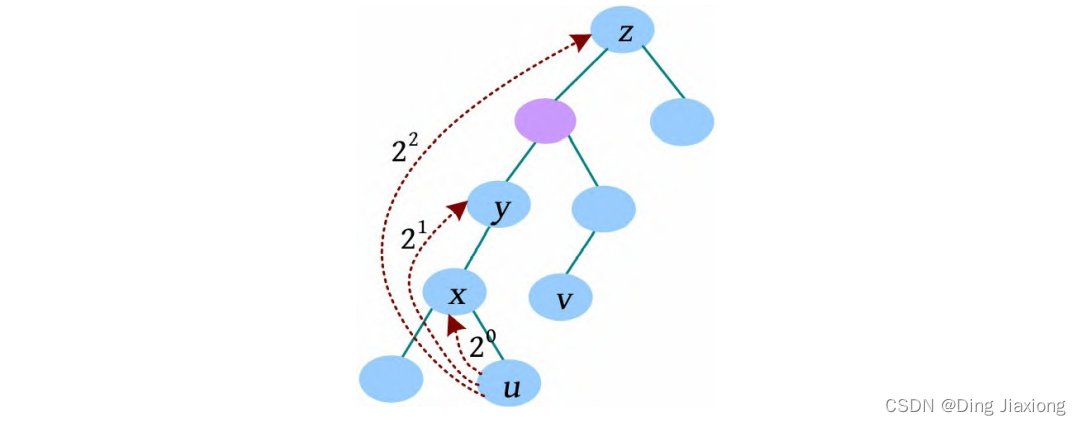
F[i , j ]表示i 的2^j 辈祖先，即i 节点向根节点走2^j 步到达的节点。可以分两个步骤：i 节点先向根节点走2^(j -1) 步得到F[i , j-1]；再从F[i , j -1]节点出发向根节点走2^(j -1) 步，得到F[F[i , j-1], j -1]，该节点为F[i , j ]。

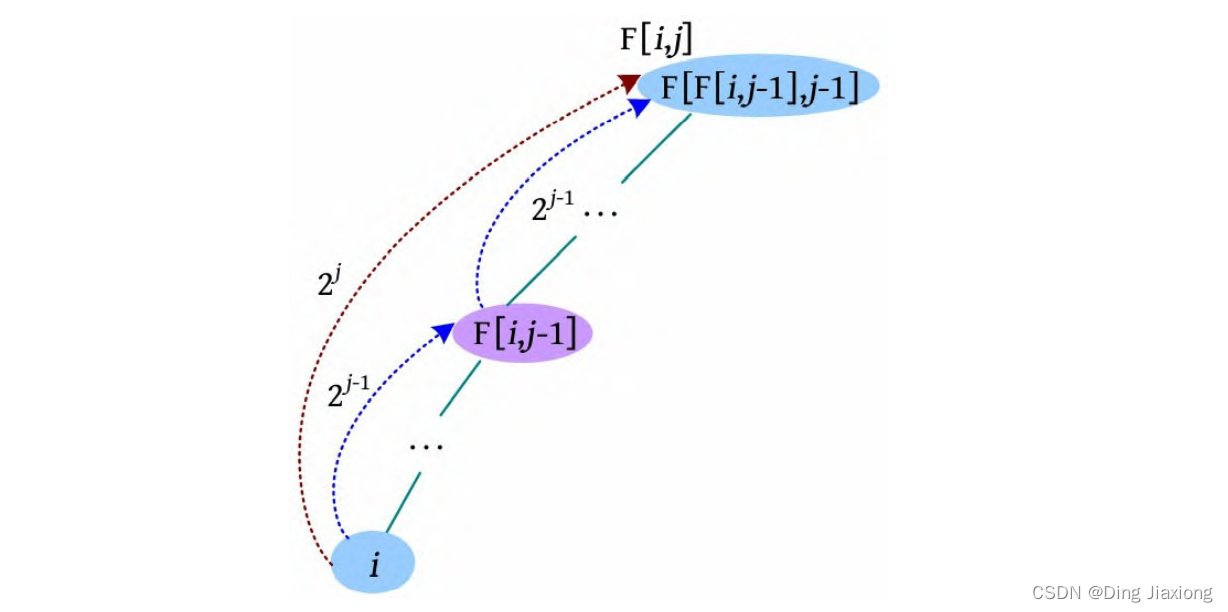
递推公式：F[i , j ]=F[F[i , j -1], j -1]，i =1, 2, …n ，j=0, 1, 2, …k ，2 k ≤n ，k =log2 n 。

① 算法设计

[1] 创建ST。

[2] 利用ST求解LCA。

② 举个栗子

和前面暴力搜索中的同步前进法一样，先让深度大的节点y 向上走到与x 同一深度，然后x、y 一起向上走。和暴力搜索不同的是，向上走是按照倍增思想走的，不是一步一步向上走的，因此速度较快。

问题一： 怎么让深度大的节点y 向上走到与x 同一深度呢？

假设y 的深度比x 的深度大，需要y 向上走到与x 同一深度，k=3，则求解过程如下。

[1] y 向上走2^3 步，到达的节点深度比x 的深度小，什么也不做。

[2] 减少增量，y 向上走2^2 步，此时到达的节点深度比x 的深度大，y 上移，y =F[y ][2]。

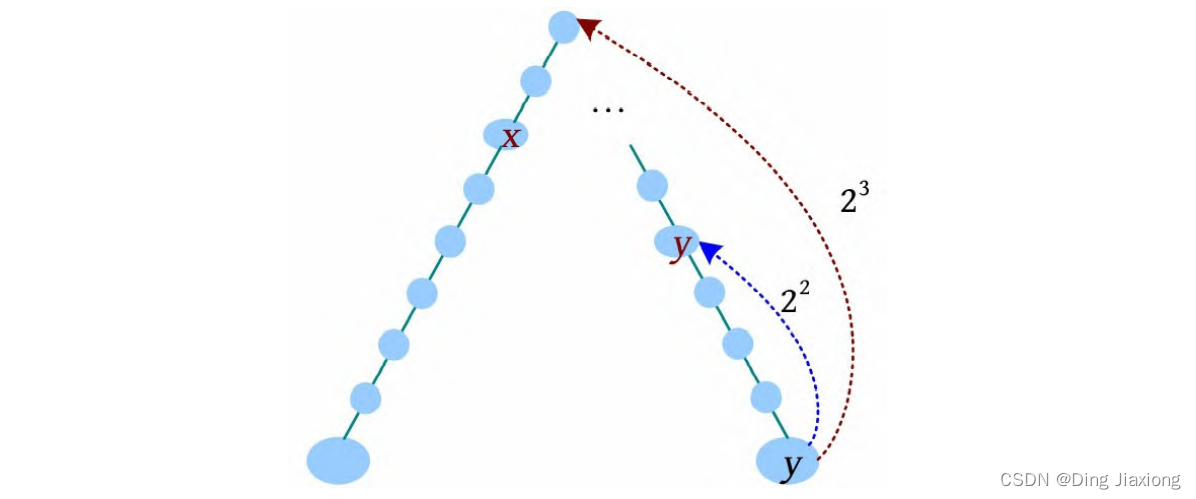
[3] 减少增量，y 向上走2^1 步，此时到达的节点深度与x 的深度相等，y 上移，y =F[y ][1]。

[4] 减少增量，y 向上走2^0 步，到达的节点深度比x 的深度小，什么也不做。此时x、y 在同一深度。

总结：按照增量递减的方式，到达的节点深度比x 的深度小时，什么也不做；到达的节点深度大于或等于x 的深度时，y 上移，直到增量为0，此时x、y 在同一深度。

问题二： x、y 一起向上走，怎么找最近的公共祖先呢？

假设x 、y 已到达同一深度，现在一起向上走，k =3，则其求解过程如下。

[1] x 、y 同时向上走2^3 步，到达的节点相同，什么也不做。

[2] 减少增量，x 、y 同时向上走2^2 步，此时到达的节点不同，x 、y 上移，x =F[x ][2]，y =F[y ][2]。

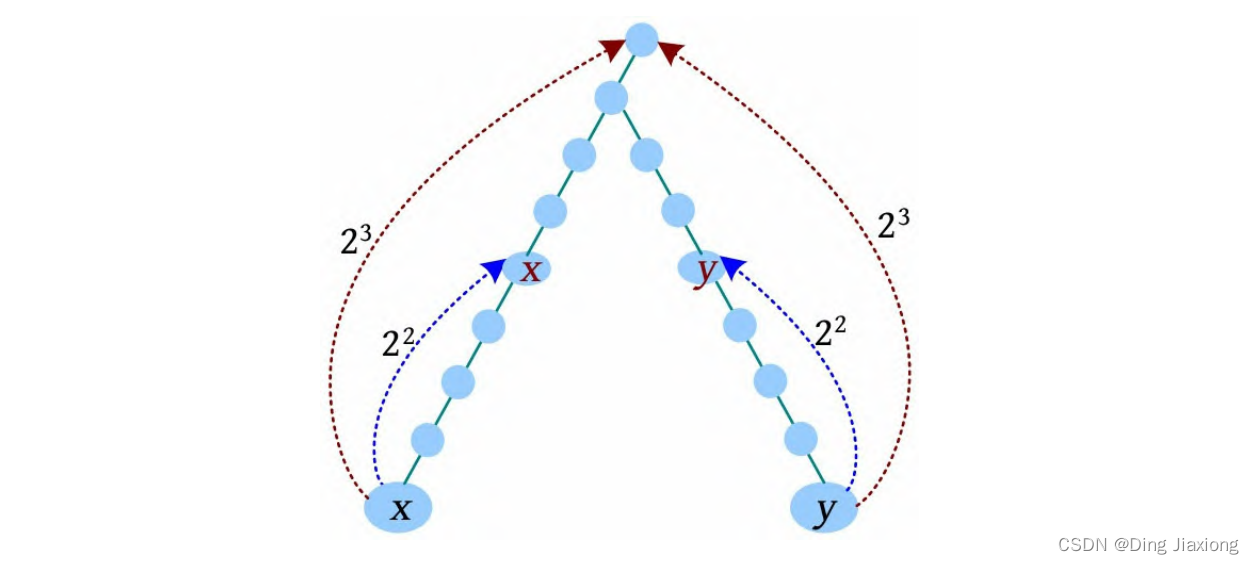
[3] 减少增量，x 、y 同时向上走2^1 步，此时到达的节点不同，x 、y 上移，x =F[x ][1]，y =F[y ][1]。

[4] 减少增量，x 、y 同时向上走2^0 步，此时到达的节点相同，什么也不做。

此时x 、y 的父节点为最近公共祖先节点，即LCA(x , y )=F[x ][0]。

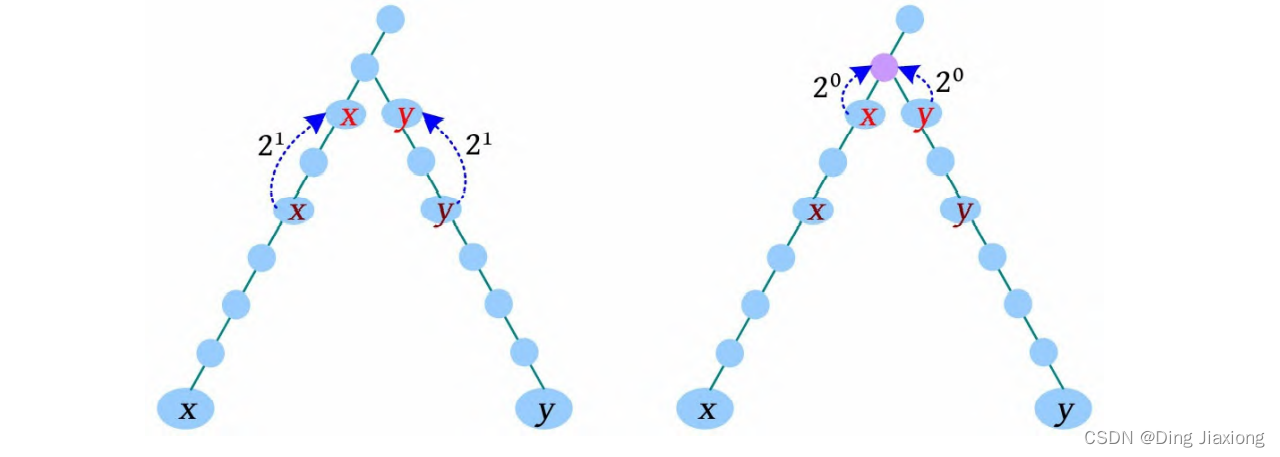
完整的求解过程如下图所示。

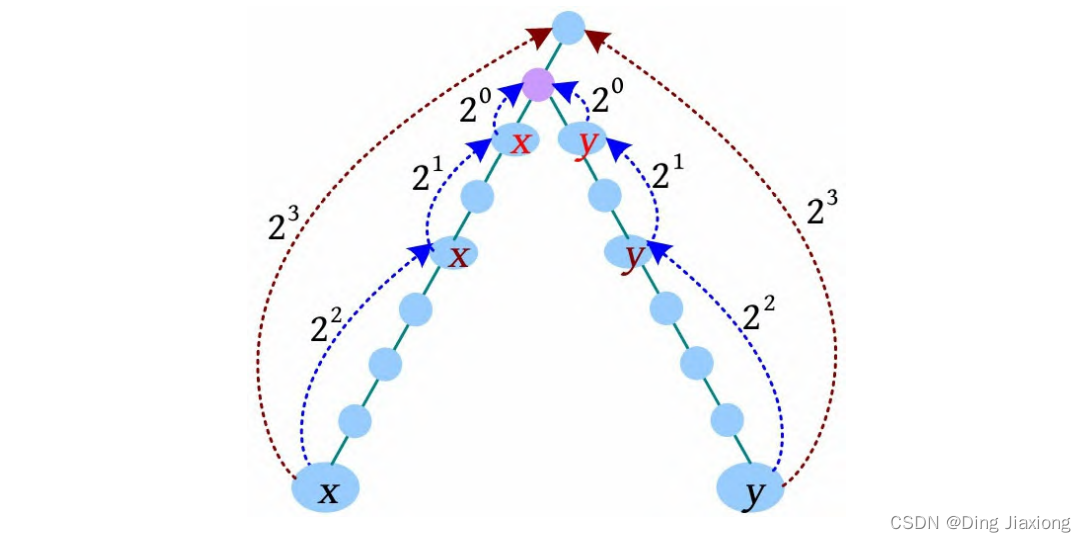
总结：按照增量递减的方式，到达的节点相同时，什么也不做；到达的节点不同时，同时上移，直到增量为0。此时x 、y 的父节点为公共祖先节点。

③ 算法实现

void ST_create(){ //构造ST
	for(int j = 1;  j <= k ; j++){
		for(int i = 1; i <= n ; i++){ //i 先走2^(j - 1) 步到达F[i][j - 1] ，再走 2^(j - 1) 步
			F[i][j] = F[F[i][j- 1]][j -1];
		}
	}
}

int LCA_st_query(int x, int y){ // 求x 、 y 的最近公共祖先
	
	if(d[x] > d[y]){ // 保证x 的深度小于或 等于y
		swap(x , y);
	}
	for(int i = k ; i >= 0 ; i --){ //y 向上走到 与 x 同一深度
		if(d[F[y][i]] >= d[x]){
			y = F[y][i];
		}
	}
	if(x == y){
		return x;
	}
	for(int i = k ; i >= 0 ; i --){ // x、y 一起向上走
		if(F[x][i] != F[y][i]){
			x = F[x][i] , y = F[y][i];
		}
	}
	return F[x][0]; //返回x 的父节点
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

④ 算法分析

采用树上倍增法求解LCA，创建ST需要O (n logn )时间，每次查询都需要O (logn )时间。一次建表、多次使用，该算法是基于倍增思想的动态规划，适用于多次查询的情况。若只有几次查询，则预处理需要O (n logn )时间，还不如暴力搜索快。

【原理3】 在线RMQ 算法

两个节点的LCA一定是两个节点之间欧拉序列中深度最小的节点，寻找深度最小值时可以使用RMQ算法。

① 完美图解

欧拉序列指在深度遍历过程中把依次经过的节点记录下来，把回溯时经过的节点也记录下来，一个节点可能被记录多次，相当于从树根开始，一笔画出一个经过所有节点的回路。

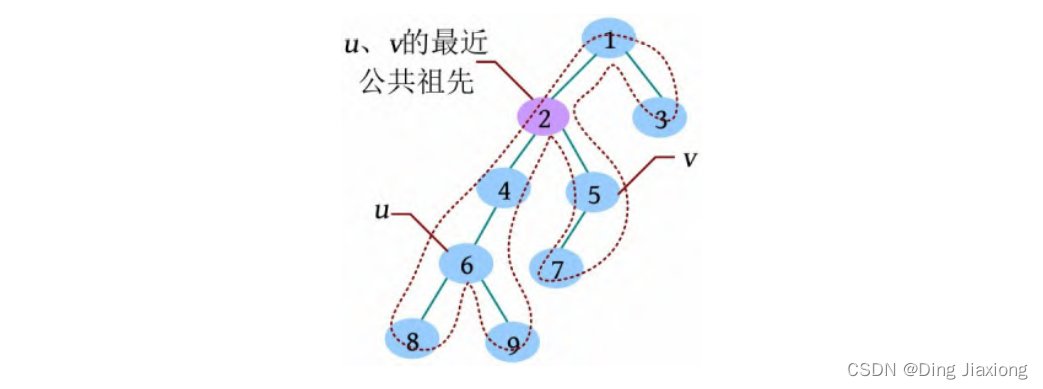
该树的欧拉序列为1 2 4 6 8 6 9 6 4 2 5 7 5 2 1 3 1，搜索时得到6和5首次出现的下标i 、j ，然后查询该区间深度最小的节点，为6和5号节点的最近公共祖先。

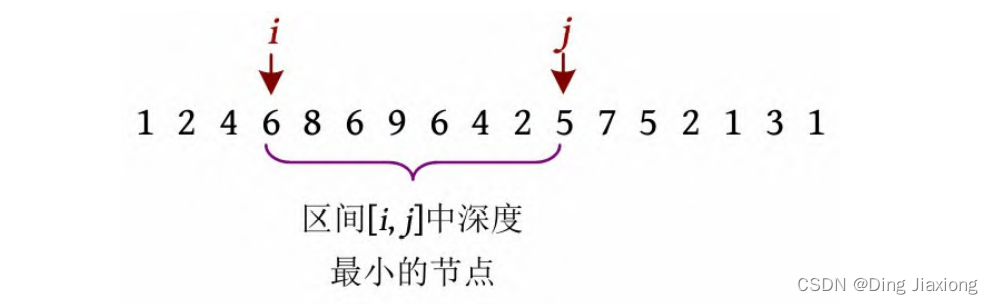
② 算法实现

[1] 深度遍历，得到3个数组：首次出现的下标是pos[]，深度遍历得到的欧拉序列是seq[]，深度是dep[]。

pos[u] = ++tot; //u 首次出现的下标
seq[tot] = u; //dfs 遍历得到的 欧拉序列
dep[tot] = d; //深度

void dfs(int u , int d){ // dfs 序
	
	vis[u] = true;
	pos[u] = ++tot; //u 首次出现的下标
	
	seq[tot] = u; //dfs 遍历得到的欧拉序列
	dep[tot] = d; //深度
	
	for(int i = head[u] ; i ; i = e[i].next){
		
		int v = e[i].to , w= e[i].c;
		if(vis[v]){
			continue;
		}
		dist[v] = dist[u] + w;
		dfs(v , d + 1);
		seq[++ tot] = u; //dfs 遍历序列
		dep[tot] = d; //深度
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

[2] 根据欧拉序列的深度，创建区间最值查询的ST。F(i , j )表示[i , i +2 j -1]区间深度最小的节点下标。

void ST_create(){ //创建 ST
	for(int i = 1;  i <= tot; i ++){ // 初始化
		F[i][0] = i; //记录下标，不是最小深度
	}
	
	int k = log2(tot);
	for(int j = 1; j <= k ; j ++){
		for(int i = 1; i <= tot - (1 << j) + 1 ; i ++){ // tot - 2 ^ j + 1
			if(dep[F[i][j - 1]] < dep[F[i + (1 << (j - 1))][j - 1]]){
				F[i][j] = F[i][j - 1];					
			}		
			else{
				F[i][j] = F[i + (1 << (j - 1))][j - 1];	
			}
		}
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

[3] 查询[l , r ]区间深度最小的节点下标，与RMQ区间查询类似。

int RMQ_query(int l , int r){ // 查询[ l ,r]  的区间最值
	
	int k  =log2(r -  l + 1);
	if(dep[F[l][k]] < dep[F[r - (1 << k ) + 1][k]]){
		return F[l][k];
	}
	else{
		return F[r - (1 << k) + 1][k]; //返回深度最小的 节点下标
	}
}
1
2
3
4
5
6
7
8
9
10

[4] 求x、y 的最近公共祖先，先得到x、y 首次出现在欧拉序列中的下标，然后查询该区间深度最小的节点的下标，根据下标读取欧拉序列的节点即可。

int LCA(int x, int y){ // 求x 、 y 的最近公共祖先
	
	int l = pos[x] , r = pos[y]; //读取第 1 次出现的下标
	if(l > r){
		swap(l , r);
	}
	return seq[RMQ_query(l , r)]; //返回节点
}
1
2
3
4
5
6
7
8

⑤ 算法分析

在线RMQ算法是基于倍增和RMQ的动态规划算法，其预处理包括深度遍历和创建ST，

需要O (n logn )时间，每次查询都需要O (1)时间。

注意：虽然都用到了ST，但是在线RMQ算法中的ST和树上倍增算法中的ST，其表达的含义是不同的，前者表示区间最值，后者表示向上走的步数。

【原理4】 Tarjan 算法

这里的Tarjan算法是用于解决LCA问题的离线算法

在线算法指每读入一个查询（求一次LCA就叫作一次查询），都需要运行一次程序得到本次查询答案。若一次查询需要 O (logn )时间，则m 次查询需要O (m logn )时间。离线算法指首先读入所有查询，然后运行一次程序得到所有查询答案。Tarjan算法利用并查集优越的时空复杂性，可以在O (n +m )时间内解决LCA问题。

① Tarjan 算法

[1] 初始化集合号数组和访问数组，fa[i ]=i ，vis[i ]=0。

[2] 从u 出发深度优先遍历，标记vis[u ]=1，深度优先遍历u 所有未被访问的邻接点，在遍历过程中更新距离，回退时更新集合号。

[3] 当u 的邻接点全部遍历完毕时，检查关于u 的所有查询，若存在一个查询u 、v ，而vis[v ]=1，则利用并查集查找v 的祖宗，找到的节点就是u 、v 的最近公共祖先。

② 举个栗子

在树中求5、6的最近公共祖先，求解过程如下。

[1] 初始化所有节点的集合号都等于自己，fa[i ]=i ，vis[i]=0。

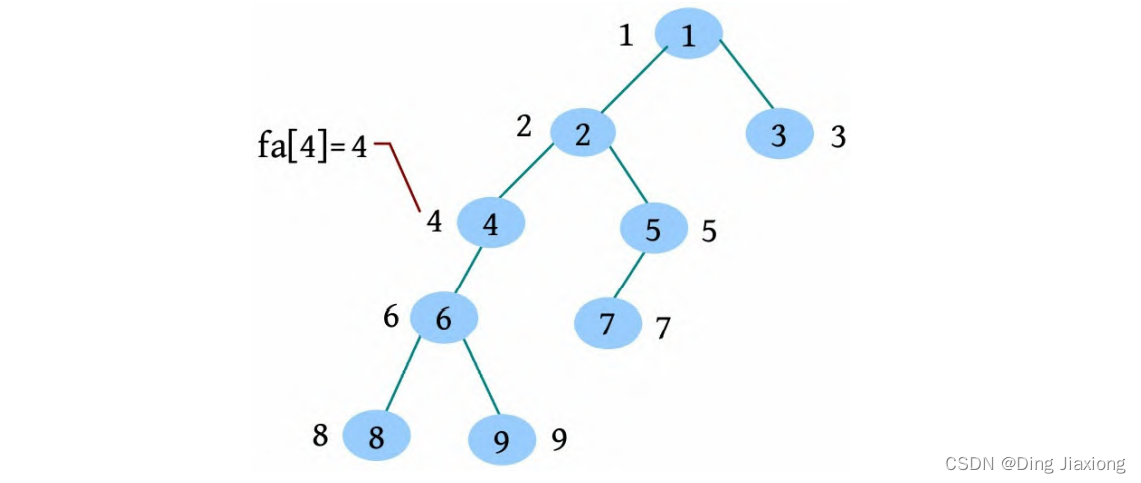
[2] 从根节点开始深度优先遍历，在遍历过程中标记vis[]=1。

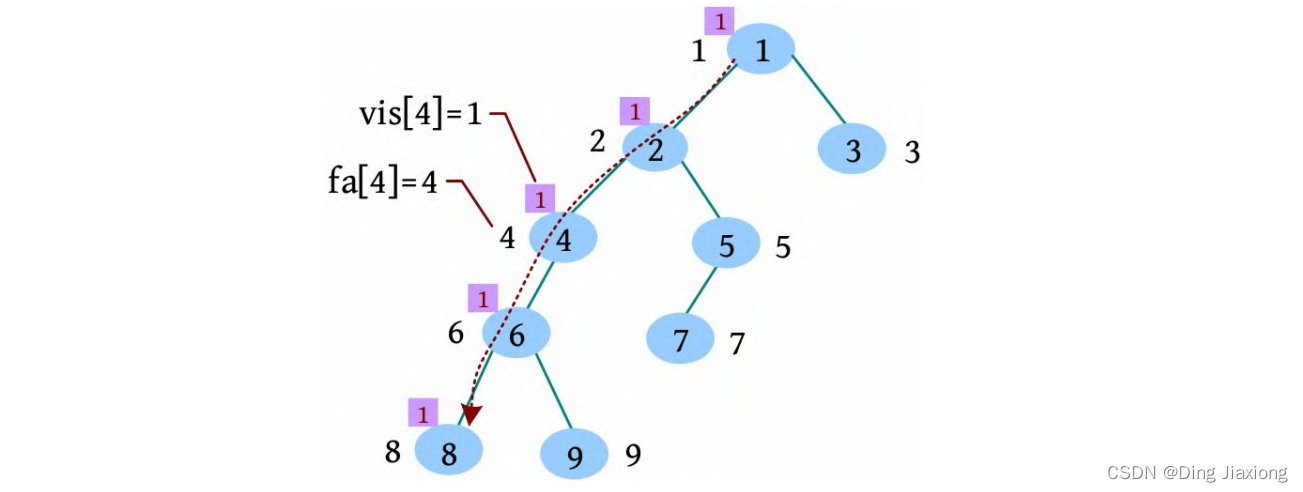
[3] 8号节点的邻接点已访问完毕，更新fa[8]=6，没有8相关的查询，回退到6。

[4] 遍历6号节点的下一个邻接点9，标记vis[9]=1，9号节点的邻接点已访问完毕，更新fa[9]=6，没有9相关的查询，回退到6。

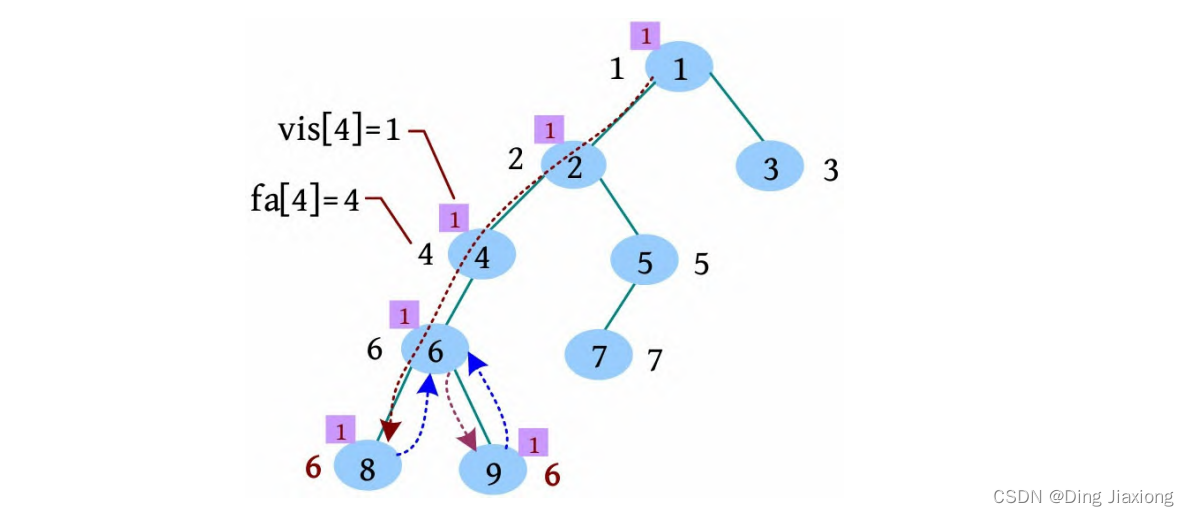
[5] 6号节点的邻接点已访问完毕，更新fa[6]=4，有6相关的查询5（查询5 6），但是vis[5]≠1，什么也不做，返回到4。

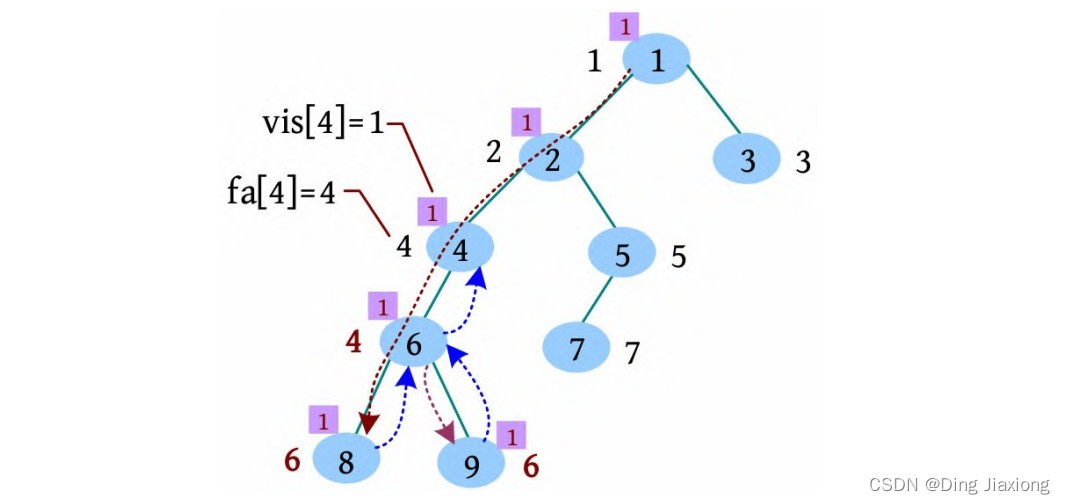
[6] 4号节点的邻接点已访问完毕，更新fa[4]=2，没有4相关的查询，返回到2。

[7] 遍历2号节点的下一个邻接点5，标记vis[5]=1，继续深度遍历到7，标记vis[7]=1，7号节点的邻接点已访问完毕，更新fa[7]=5，没有7相关的查询，回退到5。

[8] 5号节点的邻接点已访问完毕，更新fa[5]=2，有5相关的查询6（查询5 6），且vis[6]=1，此时需要从6号节点开始使用并查集查找祖宗。

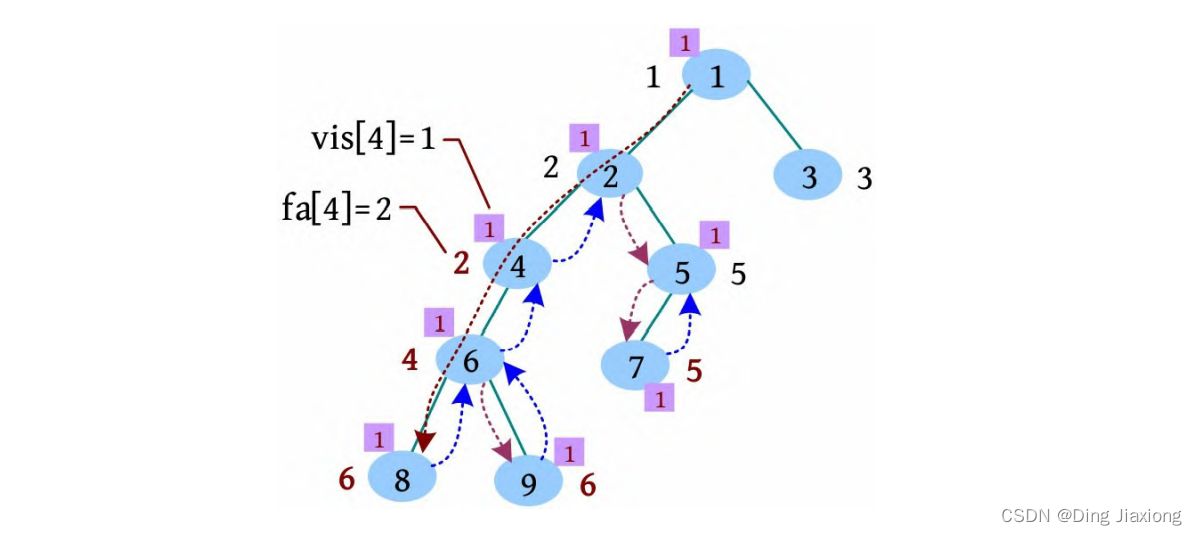
[9] 从6号节点开始利用并查集查找祖宗的的过程如下。首先判断6的集合号fa[6]=4，找4的集合号fa[4]=2，找2的集合号fa[2]=2，找到祖宗（集合号为其自身）后返回，并更新祖宗到当前节点路径上所有节点的集合号，即更新6、4的父节点fa[4]=2，fa[6]=2，此时fa[6]就是5和6的最近公共祖先。

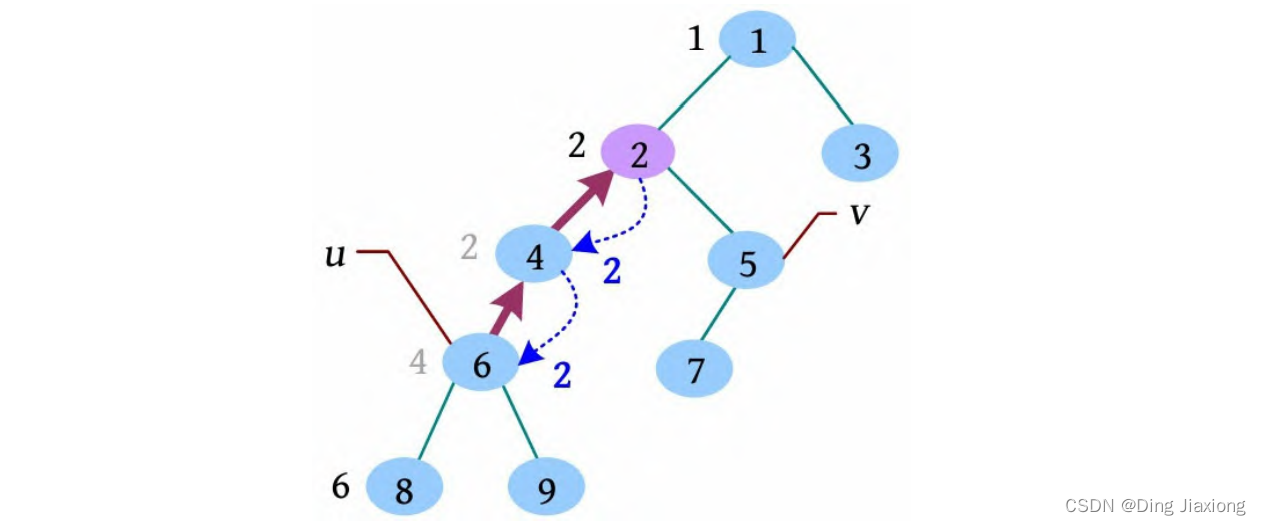
[总结]

在当前节点u 的邻接点已访问完毕时，检查u 相关的所有查询v ，若vis[v ]≠1，则什么也不做；若vis[v ]=1，则利用并查集查找v 的祖宗，lca(u , v )=fa[v ]。实际上，u 的祖宗就是u 向上查找第1个邻接点未访问完的节点，它的fa[]还没有更新，仍满足fa[i]=i ，它就是v 的祖宗。

③ 算法实现

int find(int x){ //并查集 找祖宗
	if(x != fa[x]){
		fa[x] = find(fa[x]); 
	}
	return fa[x];
}

void tarjan(int u){ // Tarjan算法
	
	vis[u] = 1;
	for(int i = head[u] ; i ; i = e[i].next){
		int v = e[i].to , w = e[i].c;
		if(vis[v]){
			continue;
		}
		dis[v] = dis[u] + w;
		tarjan(v);
		fa[v] = u;
	}
	for(int i = 0; i < query[u].size() ; i ++){ // u相关的所有查询
		int v = query[u][i];
		int id = query_id[u][i];
		
		if(vis[y]){
			int lca = find(v);
			ans[id] = dis[u] + dis[v] - 2 * dis[lca];
		}
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

④ 算法分析

离线Tarjan算法用到了并查集的优越性，m 次查询的时间为O (n+m )。