代码随想录训练营第29天|LeetCode 491.递增子序列、46.全排列、47.全排列 II

参考

代码随想录

题目一：LeetCode 491.递增子序列

这个题同样涉及到去重，但是不能再使用子集II那题中的去重方法，在那个题中用下面的代码去重：

if (i > 0 && nums[i] == nums[i - 1] && !used[i - 1]){
        continue;
1
2

这样去重的前提是已经对原来的数组进行排序，但是这个题不能对原来的数组排序。去重原理是一样的，即在同一层上已经使用过的元素就不能再使用了。这里使用unordered_set来保存每一层上使用过的元素，以此来实现去重操作。

1. 确定递归函数的参数和返回值
   参数：数组nums，指向下一个元素的startIndex
   返回值：无

vector<int> path;
vector<vector<int>> result;
void backtracking(vector<int>& nums,int startIndex);
1
2
3

2. 确定终止条件：这里可以有终止条件，也可以没有，如果有，当startIndex == nums.size()的时候就可以返回了，也可以没有是因为此时不会满足for循环了，也会退出，因此可以不写终止条件。另外，需要收集遍历路径上的满足条件的结果，因为要至少有两个元素，所以当path中的元素大于等于2时就保存当result中。

if(path.size() >= 2)	
	result.push_back(path);
1
2

3. 确定单层递归逻辑：如果当前元素在这一层上还没有用过，且满足递增关系，则将该元素加入到path中，否则不做处理，然后递归调用，遍历剩余元素。

unordered_set<int> set;
for(int i = startIndex; i < nums.size(); i++){
    if((!path.empty() && path.back() > nums[i]) || 
    set.find(nums[i]) != set.end())
        continue;
    set.insert(nums[i]);
    path.push_back(nums[i]);
    backtracking(nums,i+1);
    path.pop_back();
}
1
2
3
4
5
6
7
8
9
10

注意，上面的unordered_set set;要定义在函数内部，因为每一层对应一个集合，不能只使用一个。完整的代码实现如下：

class Solution {
public:
    void backtracking(vector<int>& nums,int startIndex){
        if(path.size() >= 2)	
	        result.push_back(path);
        unordered_set<int> set;
        for(int i = startIndex; i < nums.size(); i++){
            if((!path.empty() && path.back() > nums[i]) || 
            set.find(nums[i]) != set.end())
                continue;
            set.insert(nums[i]);
            path.push_back(nums[i]);
            backtracking(nums,i+1);
            path.pop_back();
        }
    }
    vector<vector<int>> findSubsequences(vector<int>& nums) {
        backtracking(nums,0);
        return result;
    }
private:
    vector<int> path;
    vector<vector<int>> result;
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

优化

上面用unordered_set来实现哈希，但这个题可以用数组来实现。题目中说数值范围为[-100,100]，因此定义一个大小为201，类型为bool类型的数组就可以了。将unordered_set替换为数组后的代码如下：

class Solution {
public:
    void backtracking(vector<int>& nums,int startIndex){
        if(path.size() >= 2)	
	        result.push_back(path);
        bool used[201] = {false};
        for(int i = startIndex; i < nums.size(); i++){
            if((!path.empty() && path.back() > nums[i]) || 
            used[nums[i] + 100] == true)
                continue;
            used[nums[i] + 100] = true;
            path.push_back(nums[i]);
            backtracking(nums,i+1);
            path.pop_back();
        }
    }
    vector<vector<int>> findSubsequences(vector<int>& nums) {
        backtracking(nums,0);
        return result;
    }
private:
    vector<int> path;
    vector<vector<int>> result;
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

题目二：LeetCode 46.全排列

全排列的过程抽象为如下图所示的树形结构：

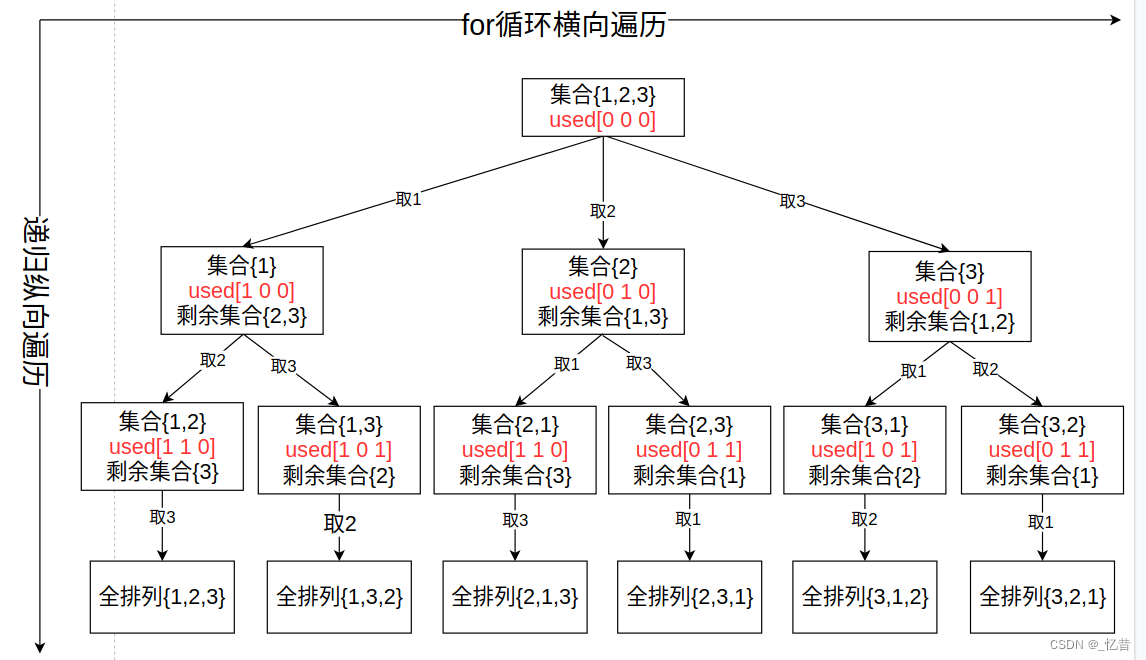
1. 确定递归函数的参数
   排列问题需要使用一个used数组来标记某个元素是否使用过，如上图中的红色部分。

vector<vector<int>> result;
vector<int> path;
void backtracking (vector<int>& nums, vector<bool>& used)
1
2
3

2. 确定递归终止条件：可以从上图看出，最终要收集的是叶子节点，当path.size() == nums.size()的时候就说明到了叶子节点了，即可以保存结果了。

if (path.size() == nums.size()) {
    result.push_back(path);
    return;
}
1
2
3
4

3. 确定单层搜索逻辑：在排列的for循环中，每次都要从头开始搜索，如果某个元素已经使用过了就跳过该元素。

for (int i = 0; i < nums.size(); i++) {
    if (used[i] == true) continue; // path里已经收录的元素，直接跳过
    used[i] = true;
    path.push_back(nums[i]);
    backtracking(nums, used);
    path.pop_back();
    used[i] = false;
}
1
2
3
4
5
6
7
8

完整的代码实现如下：

class Solution {
public:
    void backtracking(vector<int>& nums,vector<bool>& used)
    {
        if(path.size() == nums.size()){
            result.push_back(path);
            return;
        }
        for(int i = 0; i < nums.size(); i++){
            if(used[i] == true) continue;
            used[i] = true;
            path.push_back(nums[i]);
            backtracking(nums,used);
            used[i] = false;
            path.pop_back();
        }
    }
    vector<vector<int>> permute(vector<int>& nums) {
        vector<bool> used(nums.size(),false);
        backtracking(nums,used);
        return result;
    }
private:
    vector<int> path;
    vector<vector<int>> result;
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

题目三：LeetCode 47.全排列II

这个题在上一个题的基础上加入去重操作，去重过程如下图所示：

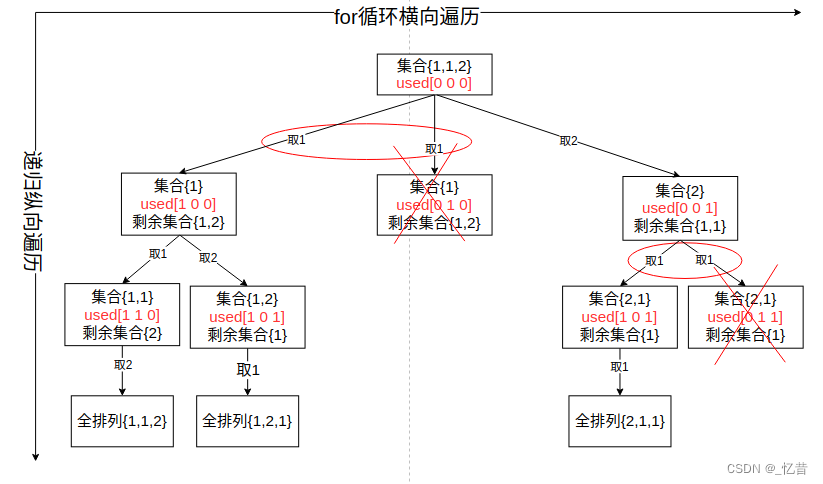
可以看出，同样是在同一层上使用过的元素不能再使用。其实，在纵向遍历过程中去重也是可以的，但是为了和组合一致，还是使用在树层上去重，且这种方式效率更高。代码实现如下：

class Solution {
public:
void backtracking(vector<int>& nums,vector<bool>& used)
    {
        if(path.size() == nums.size()){
            result.push_back(path);
            return;
        }
        for(int i = 0; i < nums.size(); i++){
            if(i > 0 && nums[i] == nums[i-1] && used[i-1] == false) continue;
            if(used[i] == true) continue;
            used[i] = true;
            path.push_back(nums[i]);
            backtracking(nums,used);
            used[i] = false;
            path.pop_back();
        }
    }
    vector<vector<int>> permuteUnique(vector<int>& nums) {
        vector<bool> used(nums.size(),false);
        sort(nums.begin(),nums.end());
        backtracking(nums,used);
        return result;
    }
private:
    vector<int> path;
    vector<vector<int>> result;
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

其中的去重语句为：

if(i > 0 && nums[i] == nums[i-1] && used[i-1] == false) continue;
1

如果将上面的used[i-1] == false改为used[i-1] == true则就是在纵向遍历中去重。