LeetCode 623. 在二叉树中增加一行

题目：

链接：LeetCode 623. 在二叉树中增加一行
难度：中等

给定一个二叉树的根 root 和两个整数 val 和 depth ，在给定的深度 depth 处添加一个值为 val 的节点行。

注意，根节点 root 位于深度 1 。

加法规则如下:

• 给定整数 depth，对于深度为 depth - 1 的每个非空树节点 cur ，创建两个值为 val 的树节点作为 cur 的左子树根和右子树根。
• cur 原来的左子树应该是新的左子树根的左子树。
• cur 原来的右子树应该是新的右子树根的右子树。
• 如果 depth == 1 意味着 depth - 1 根本没有深度，那么创建一个树节点，值 val 作为整个原始树的新根，而原始树就是新根的左子树。

示例 1:

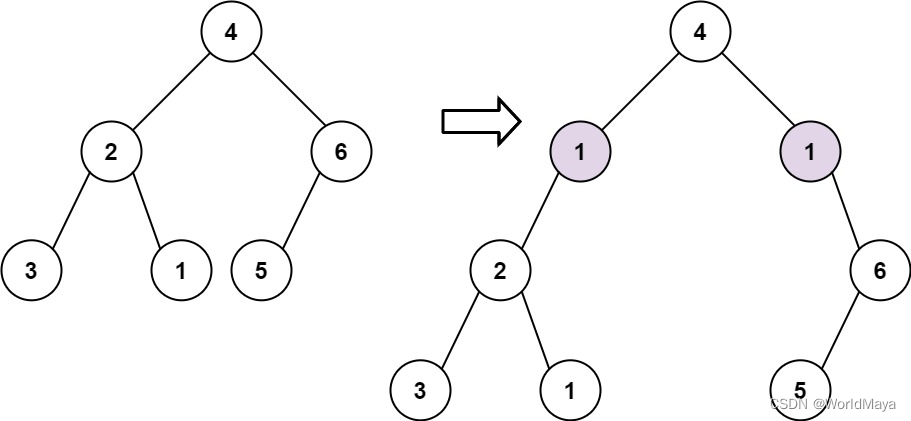
输入: root = [4,2,6,3,1,5], val = 1, depth = 2
输出: [4,1,1,2,null,null,6,3,1,5]

示例 2:

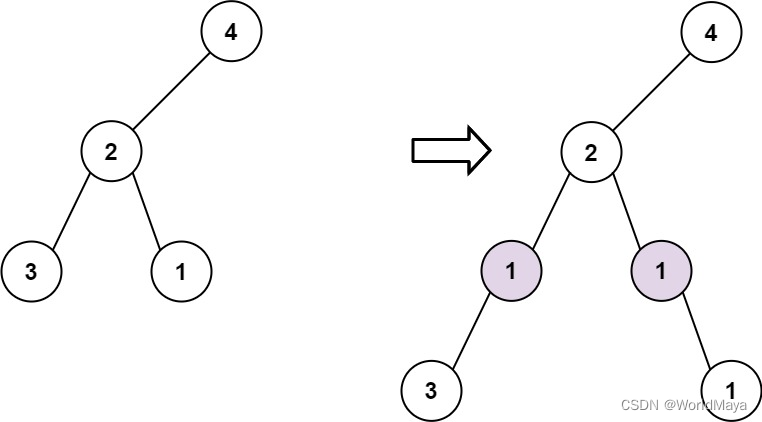
输入: root = [4,2,null,3,1], val = 1, depth = 3
输出: [4,2,null,1,1,3,null,null,1]

提示:

• 节点数在 [1, 104] 范围内
• 树的深度在 [1, 104]范围内
• -100 <= Node.val <= 100
• -105 <= val <= 105
• 1 <= depth <= the depth of tree + 1

方法一：

解题思路：

二叉树层序遍历（广度优先搜索）。以层序（深度）遍历该二叉树，用一个队列存储当前层上一层的节点，若遍历到给定层则添加节点行给上一层作新子树根，若未遍历到给定层则让下一层节点进入队列、上一层节点弹出队列，继续遍历。

代码一：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* addOneRow(TreeNode* root, int val, int depth) {
        if(depth == 1) {  //给定深度是1时，替换树根
            TreeNode* temp = new TreeNode(val);
            temp->left = root;
            root = temp;
        }
        else {  //二叉树层序遍历
            int i = 2;  //当前遍历的深度
            queue<TreeNode*> q;  //队列q存储当前层的上一层的节点
            q.push(root);
            while(!q.empty()) {
                if(i == depth) {  //在给定的深度添加节点行
                    while(!q.empty()) {
                        TreeNode* temp = q.front();
                        TreeNode* temp1 = new TreeNode(val);  //新左子树根
                        TreeNode* temp2 = new TreeNode(val);  //新右子树根
                        temp1->left = temp->left;
                        temp->left = temp1;
                        temp2->right = temp->right;
                        temp->right = temp2;
                        q.pop();
                    }
                    break;
                }
                else {  //未到给定深度时继续遍历下一层
                    int size = q.size();
                    while(size--) {
                        TreeNode* temp = q.front();
                        if(temp->left != nullptr) q.push(temp->left);
                        if(temp->right != nullptr) q.push(temp->right);
                        q.pop();
                    }
                    i++;
                }
            }
        }
        return root;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52

时间复杂度O(n)，空间复杂度O(n)。

方法二：

解题思路：

深度优先搜索。将深度通过递归传递下去，每层递归深度-1，相当于把子树作为新的原始树处理。

代码二：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* addOneRow(TreeNode* root, int val, int depth) {
        if(depth == 1) {
            TreeNode* temp = new TreeNode(val);
            temp->left = root;
            root = temp;
            return root;
        }
        else if(depth == 2) {
            TreeNode* temp1 = new TreeNode(val);
            TreeNode* temp2 = new TreeNode(val);
            temp1->left = root->left;
            root->left = temp1;
            temp2->right = root->right;
            root->right = temp2;
            return root;
        }
        else {
            if(root->left != nullptr) addOneRow(root->left, val, depth-1);
            if(root->right != nullptr) addOneRow(root->right, val, depth-1);
            return root;
        }
    }
};


//也可以写成如下形式
class Solution {
public:
    TreeNode* add(TreeNode* root, int val, int depth, int i) {
        if(i == depth-1) {
            TreeNode* temp1 = new TreeNode(val);
            TreeNode* temp2 = new TreeNode(val);
            temp1->left = root->left;
            root->left = temp1;
            temp2->right = root->right;
            root->right = temp2;
            return root;
        }
        else {
            if(root->left != nullptr) add(root->left, val, depth, i+1);
            if(root->right != nullptr) add(root->right, val, depth, i+1);
            return root;
        }
    }
    TreeNode* addOneRow(TreeNode* root, int val, int depth) {
        if(depth == 1) {
            TreeNode* temp = new TreeNode(val);
            temp->left = root;
            root = temp;
            return root;
        }
        else return add(root, val, depth, 1);
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67

时间复杂度O(n)，空间复杂度O(n)。