-
数据结构--单链表
1.定义
由于顺序表的插入删除操作需要移动大量的元素,影响了运行效率,因此引入了线性表的链式存储——单链表。单链表通过一组任意的存储单元来存储线性表中的数据元素,不需要使用地址连续的存储单元,因此它不要求在逻辑上相邻的两个元素在物理位置上也相邻。
2.特点
- 单链表不要求逻辑上相邻的两个元素在物理位置上也相邻,因此不需要连续的存储空间。
- 单链表是非随机的存储结构,即不能直接找到表中某个特定的结点。查找某个特定的结点时,需要从表头开始遍历,依次查找。
- 对于每个链表结点,除了存放元素自身的信息外,还需要存放一个指向其后继的指针。
3.代码
1.lishh
//头文件 ".h",存放结构或者函数的声明
//带头结点单链表,逻辑相邻,物理不一定相邻,为了找到下一个节点,就必须增加下一个节点的地址
//尾节点:最后一个节点,在单链表中,尾节点的next为NULL,NULL是单链表的结尾标志
//头结点:其数据域不使用或者存放链表长度.其作用,相对于一个标杆,简化操作- #pragma once
- typedef int ElemType;
- typedef struct Node
- {
- ElemType data;//数据
- struct Node* next;//后继指针
- }Node,*List;//List == Node *
- //typedef Node* List;//List == Node *
- //List本质是Node*,但含义不同,List表示一条链表,Node*表示一个节点的地址
- //初始化plist
- void InitList(List plist);
- //书上的写法
- void InitList(List *pplist);
- //往plist中头部插入数字val
- bool Insert_head(List plist, ElemType val);
- //往plist中的尾部插入数字val
- bool Insert_tail(List plist , ElemType val);
- //在plist中查找val值,找到返回该节点地址,失败返回NULL
- Node* Search(List plist, ElemType val);
- //删除plist中的第一个val
- bool DeleteVal(List plist, ElemType val);
- //判断plist是否为空链表(没有数据节点)
- bool IsEmpty(List plist);
- //获取plist长度,数据节点的个数
- int GetLength(List plist);
- //获取plist链表的pos位置的值
- //int GetElem(List plist, int pos);//设计有问题:无法清晰的表示出错
- bool GetElem(List plist,int pos,int *rtval);//rtval:输出参数
- //获取val的前驱
- Node* Prior(List plist, ElemType val);
- //获取val的后继
- Node* Next(List plist, ElemType val);
- //输出plist的所有数据
- void Show(List plist);
- //清空数据
- void Clear(List plist);
- //销毁
- void Destroy(List plist);
- //逆置,考试非常多
- void Reverse(List plist);
2.list.cpp
1.初始化plist
通常会用头指针来标识一个单链表,头指针为NULL时表示一个空表。但是,为了操作方便,会在单链表的第一个结点之前附加一个结点,称为头结点。头结点的数据域可以不设任何信息,也可以记录表长等信息。头结点的指针域指向线性表的第一个元素结点。
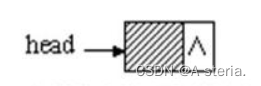
空的带头节点的单链表

含有三个结点的带头结点的点链表
头结点和头指针的区分:不管带不带头结点,头指针始终指向单链表的第一个结点,而头结点是带头结点的单链表中的第一个结点,结点内通常不存储信息。
那么单链表的初始化操作就是申请一个头结点,将指针域置空。- void InitList(List plist)
- {
- assert(plist != NULL);
- //头结点的数据不使用 plist->data可以不处理
- plist->next = NULL;
- }
2.书上的写法
- void InitList(List* pplist)
- {
- assert(pplist != NULL);
- *pplist = (Node*)malloc(sizeof(Node));//动态创建头结点
- assert(*pplist != NULL);
- if (*pplist == NULL)
- return;
- (*pplist)->next = NULL;
- }
3.往plist中头部插入数字val
所谓头插法建立单链表是说将新结点插入到当前链表的表头,即头结点之后。如图所示:
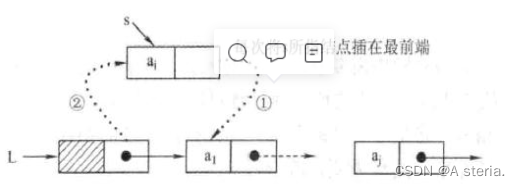
算法思想:首先初始化一个单链表,其头结点为空,然后循环插入新结点*s:将s的next指向头结点的下一个结点,然后将头结点的next指向s。
- bool Insert_head(List plist, ElemType val)//O(1)
- {
- //1.动态创建一个新节点
- Node* p = (Node*)malloc(sizeof(Node));
- assert(p != NULL);
- if (p == NULL)
- return false;
- //2.把数据val存放到新节点
- p->data = val;
- //3.把新节点插入在头结点的后面
- p->next = plist->next;
- plist->next = p;
- return true;
- }
4.往plist中的尾部插入数字val
需要指出的是,头插法建立的单链表中结点的次序和输入数据的顺序不一致,是相反的。若希望两者的顺序是一致的,则可采用尾插法建立单链表。
所谓尾插法建立单链表,就是将新结点插入到当前链表的表尾。如下图所示:
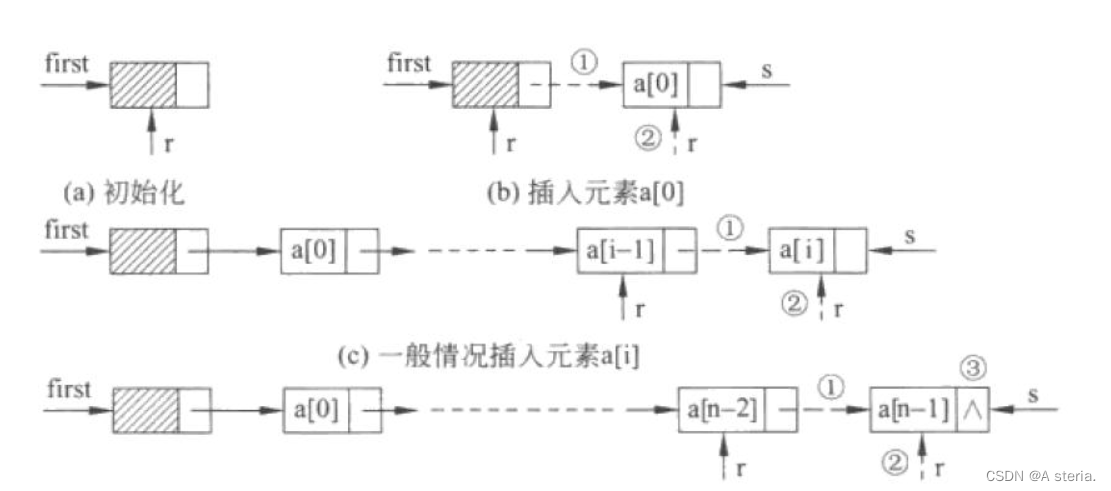
最后情况插入元素a[n-1],需将终结点的指针域置空
- bool Insert_tail(List plist, ElemType val)//O(n)
- {
- //1.动态创建新节点
- Node* p = (Node*)malloc(sizeof(Node));
- assert(p != NULL);
- if (p == NULL)
- return false;
- // 2.把值存放到新节点
- p->data = val;//p->next = NULL;
- // 3.找到链表尾巴
- Node* q;
- for (q = plist; q->next != NULL; q = q->next)
- ;
- // 4.把新节点插在尾节点的后面,把p插入在q的后面
- p->next = q->next;//p->next = NULL;
- q->next = p;
- return true;
- }
5.在plist中查找val值,找到返回该节点地址,失败返回NULL
查找值val在单链表L中的结点指针。
算法思想:从单链表的第一个结点开始,依次比较表中各个结点的数据域的值,若某结点数据域的值等于val,则返回该结点的指针;若整个单链表中没有这样的结点,则返回空。
- Node* Search(List plist, ElemType val)
- {
- for (Node* p = plist->next; p != NULL; p = p->next)
- {
- if (p->data == val)//找到了
- return p;
- }
- return NULL;//没有找到
- }
6.删除plist中的第一个val
算法思想:先检查删除位置的合法性,然后从头开始遍历,找到表中val结点,即被删除结点的前驱结点*p,被删除结点为*q,修改*p的指针域,将其指向*q的下一个结点,最后再释放结点*q的存储空间。
- bool DeleteVal(List plist, ElemType val)
- {
- //1.找val的前驱
- Node* p = Prior(plist,val);//指向前驱节点
- if (p == NULL)//没有val
- return false;
- //free(p->next);//错误
- //p->next = p->next->next;
- Node* q = p->next;//标记需要删除的节点
- p->next = q->next;//p->next = p->next->next;将q从链表中剔除
- free(q);//释放节点
- return true;
- }
7.判断plist是否为空链表(没有数据节点)
算法思想:要判断带头结点的单链表是否为空,只需要看头结点的指针域即可,如果头结点的指针域为空,即单链表中只有一个头结点,那么该单链表为空表。
- bool IsEmpty(List plist)
- {
- return plist->next == NULL;//等同下面的if else
- /*if (plist->next == NULL)
- return true;
- else
- return false;*/
- }
8.获取plist长度,数据节点的个数
算法思想:声明一个指针p,p指向头结点指向的第一个结点,如果p指向的结点不为空,那么长度加一,将p指向下一个结点,直到遍历到最后一个结点为止。
- int GetLength(List plist)
- {
- int count = 0;//计数器
- for (Node* p = plist->next; p != NULL; p = p->next)
- count++;
- return count;
- }
9.获取plist链表的pos位置的值
- //int GetElem(List plist, int pos)//设计有问题
- //{
- // if (pos < 0 || pos >= GetLength(plist))//下标不存在
- // return -1;//不可以,可能和正常的值冲突
- //}
- bool GetElem(List plist, int pos, int* rtval)//rtval:输出参数
- {
- if (pos < 0 || pos >= GetLength(plist))//出错
- return false;
- Node* p=plist->next;
- for (int i=0; i < pos; p = p->next, i++)
- {
- ;
- }
- *rtval = p->data;
- return true;
- }
10.获取val的前驱
- Node* Prior(List plist, ElemType val)
- {
- for (Node* p = plist; p != NULL; p = p->next)//bug
- {
- if (p->next->data == val)//找到了
- return p;
- }
- return NULL;//失败了
- }
11.获取val的后继
- Node* Next(List plist, ElemType val)
- {
- for (Node* p = plist->next; p != NULL; p = p->next)
- {
- if (p->data == val)
- return p->next;
- }
- return NULL;
- }
12.输出plist的所有数据
算法思想:声明一个指针p,从头结点指向的第一个结点开始,如果p不为空,那么就输出当前结点的值,并将p指向下一个结点,直到遍历到最后一个结点为止。
- void Show(List plist)
- {
- for (Node* p = plist->next; p != NULL; p = p->next)//遍历所有的数据节点
- {
- printf("%d ",p->data);
- }
- printf("\n");
- }
13.清空数据
- void Clear(List plist)
- {
- Destroy(plist);
- }
14.销毁
- void Destroy1(List plist)
- {
- if (plist == NULL || plist->next == NULL)
- return;
- Node* p = plist->next;
- Node* q;
- plist->next = NULL;
- while (p != NULL)
- {
- q = p->next;
- free(p);
- p = q;
- }
- }
- void Destroy(List plist)
- {
- Node* p;//指向第一个数据节点
- while (plist->next != NULL)//还有数据结构
- {
- p = plist->next;
- plist->next = p->next;//剔除p
- free(p);
- }
- }
3.test.cpp
- //测试文件,测试用例
- #include
- #include "list.h"
- //#include
//必须安装vld,如果没有安装不能使用 - //实现两个集合的并集,A=AUB(相同的部分取一次,不同部分全取)
- //例如A={1,2,3,4};B={5,3,1,6};结果={1,2,3,4,5,6};
- void Merge(List plistA, List plistB)
- {
- //算法:遍历plistB,查看当前值在plistA中是否存在,如果存在则什么都不做,
- //不存在则将值插入到plistA中
- int val;
- for (int i = 0; i < GetLength(plistB); i++)
- {
- GetElem(plistB,i,&val);//获取plistB,i下标的值
- if (Search(plistA, val) == NULL)//不存在
- {
- Insert_tail(plistA,val);
- }
- }
- }
- int main()
- {
- Node headA;
- Node headB;
- InitList(&headA);
- InitList(&headB);
- Insert_tail(&headA, 1);
- Insert_tail(&headA, 2);
- Insert_tail(&headA, 3);
- Insert_tail(&headA, 4);
- Show(&headA);
- Insert_tail(&headB, 5);
- Insert_tail(&headB, 3);
- Insert_tail(&headB, 1);
- Insert_tail(&headB, 6);
- Show(&headB);
- Merge(&headA,&headB);
- printf("合并后的值\n");
- Show(&headA);
- Show(&headB);
- Destroy(&headA);
- Destroy(&headB);
- return 0;
- }
结果:
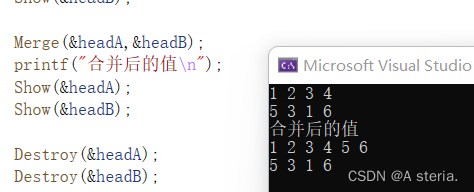
-
相关阅读:
JAVA安装教程 (windows)
AC自动机
点对点协议PPP
RADIUS协议基础原理
你应该在 Kubernetes 中运行有状态的应用程序吗?
vue学习31~39(列表过滤+列表排序+vue检测data中的数据+收集表单数据+过滤器)
【Spring Boot】专栏合集,快速入门大全
类的生命周期
instanceOf原理及手动实现
Redis入门讲解(介绍、安装、常用命令)
- 原文地址:https://blog.csdn.net/m0_59052131/article/details/127990576
