堆排序(算法实现)

堆排序-算法实现

前面介绍了堆的基本功能实现(https://blog.csdn.net/m0_46343224/article/details/127986662)，了解了堆，这里用堆实现排序

1. 向上调整和向下调整比较

思考：向上调整和向下调整哪个更优？

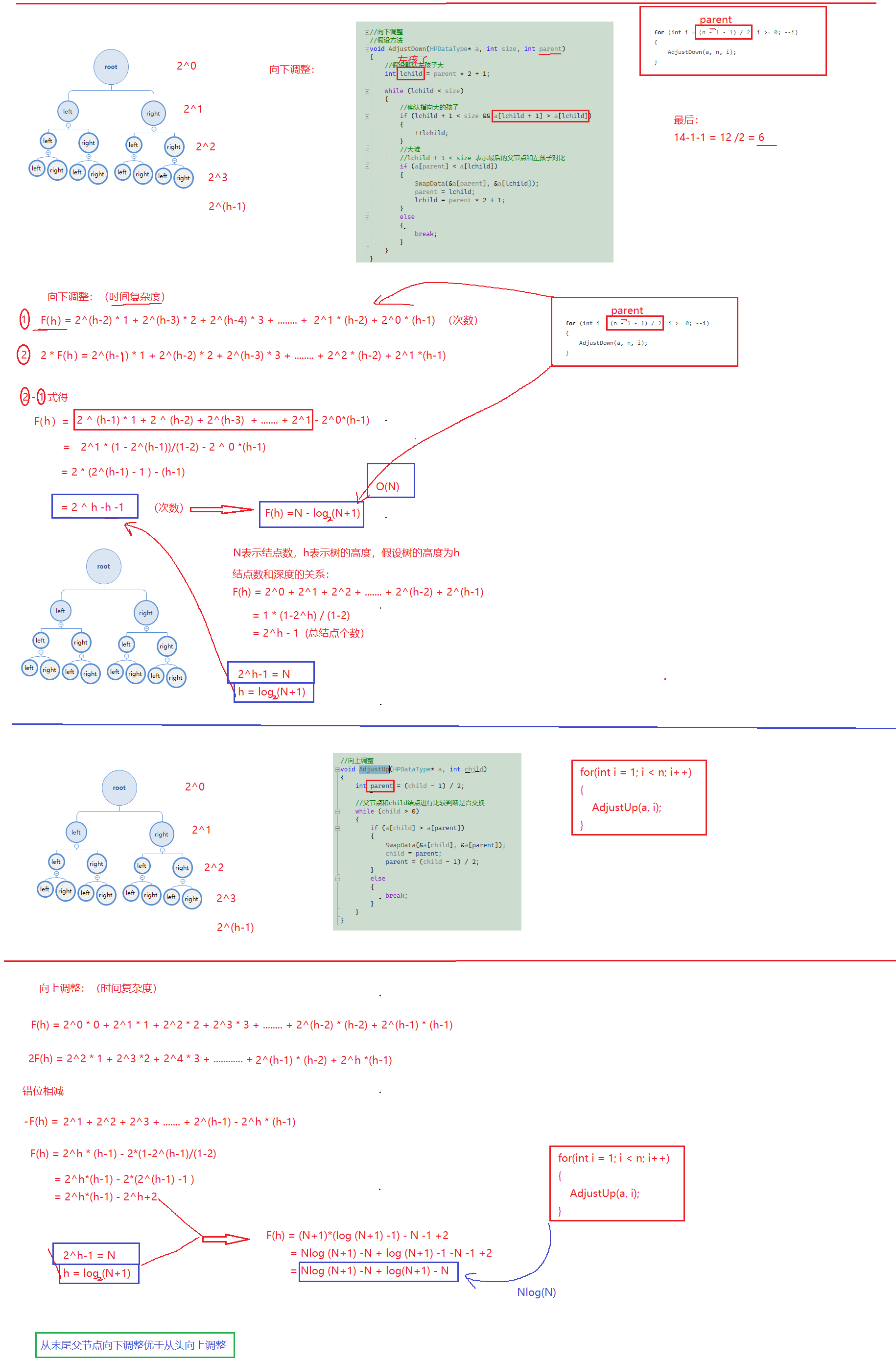
此图解析：向上调整的时间复杂度：O(N*log₂(N));向下调整的时间复杂度：O(N)；则从尾向下调整优于向上调整

2. 堆排序

堆排序思路：

升序：首先建大堆，然后交换首尾数据（也就是把最大的数据放在尾部，再从头向下调整size-1个数据（也就是不对其交换后的最大的数据调整）

降序：首先建小堆，然后交换首尾数据（也就是把最大的数据放在尾部，再从头向下调整size-1个数据（也就是不对其交换后的最大的数据调整）

1. 升序

void SwapData(int* a, int* b)
{
	int tmp = *a;
	*a = *b;
	*b = tmp;
}

void AdjustDownSortAscending(int* a, int size, int parent)
{
	//假设默认左孩子大
	int lchild = parent * 2 + 1;

	while (lchild < size)
	{
		//确认指向大的孩子
		if (lchild + 1 < size && a[lchild + 1] > a[lchild])
		{
			++lchild;
		}
		//大堆
		//lchild + 1 < size 表示最后的父节点和左孩子对比
		if (a[parent] < a[lchild])
		{
			SwapData(&a[parent], &a[lchild]);
			parent = lchild;
			lchild = parent * 2 + 1;
		}
		else
		{
			break;
		}
	}
}

void HeapSortAscending(int* a, int size)
{
	//建大堆(从尾元素父节点开始)
	for (int i = (size - 1 - 1) / 2; i >= 0; --i)
	{
		AdjustDownSortAscending(a, size, i);
	}

	int heapend = size - 1;
	while (heapend > 0)
	{
		SwapData(&a[0], &a[heapend]);
        //从首开始向下调整
		AdjustDownSortAscending(a, heapend, 0);
		heapend--;
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51

2. 降序

void SwapData(int* a, int* b)
{
	int tmp = *a;
	*a = *b;
	*b = tmp;
}

void AdjustDownSortDescending(int* a, int size, int parent)
{
	//假设默认左孩子大
	int lchild = parent * 2 + 1;

	while (lchild < size)
	{
		//确认指向大的孩子
		if (lchild + 1 < size && a[lchild + 1] < a[lchild])
		{
			++lchild;
		}
		//大堆
		//lchild + 1 < size 表示最后的父节点和左孩子对比
		if (a[parent] > a[lchild])
		{
			SwapData(&a[parent], &a[lchild]);
			parent = lchild;
			lchild = parent * 2 + 1;
		}
		else
		{
			break;
		}
	}
}

void HeapSortDescending(int* a, int size)
{
	//建小堆(从尾元素父节点开始)
	for (int i = (size - 1 - 1) / 2; i >= 0; --i)
	{
		AdjustDownSortDescending(a, size,i);
	}

	int heapend = size - 1;
	while (heapend > 0)
	{
		SwapData(&a[0], &a[heapend]);
        //从首开始向下调整
		AdjustDownSortDescending(a, heapend, 0);
		heapend--;
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51

为什么升序建立大堆，降序建立小堆?

我们知道大堆小堆都不是连续递减或递增的，拿升序来说：如果建立小堆，那么我们不一定数据连续递增的情况时，这样就增加的时间复杂度，本来可以在O(N*log₂(N))时间解决，但是这里不连续递增，就要对没有连续递增的位置上再次调整。降序建立大堆也是一样提高了不必的时间成本