【OpenCV 例程 300篇】248. 特征描述之HOG描述符

『youcans 的 OpenCV 例程300篇 - 总目录』

【youcans 的 OpenCV 例程 300篇】248. 特征描述之HOG描述符

1. 方向梯度直方图

方向梯度直方图（Histogram of Oriented Gradient, HOG）使用梯度方向的分布作为特征来构造描述符，应用非常广泛。
梯度的幅值是边缘和角点检测的基础，梯度的方向也包含着丰富的图像特征。HOG的基本思想，就是图像的局部特征可以用梯度幅值和方向的分布描述。HOG的基本方法是，将图像划分成多个单元格，计算单元格的方向梯度直方图，把每个单元格的直方图连接起来构造为HOG特征向量。
HOG描述符的向量维数不是固定不变的，取决于检测图像大小和单元格的大小。HOG描述符不具有尺度和旋转不变性，但具有有良好的几何和光学不变性，特别适合人体检测。

2. OpenCV 的 HOGDescriptor 类

OpenCV提供了cv::HOGDescriptor类实现HOG描述符。在Python语言中，OpenCV提供了HOG类的接口函数cv.HOGDescriptor。

函数原型

cv.HOGDescriptor(_winSize, _blockSize, _blockStride, _cellSize, _nbins) → retval
hog.compute(img[, _winStride=Size(), _padding=Size()]) → descriptors

参数说明
 winSize：检测窗口大小，形如(w,h)的元组，默认值(64,128)。
 blockSize：子块的大小，形如(w,h)的元组，默认值(16,16)。
 blockStride：子块的滑动步长，形如(w,h)的元组，默认值(8,8)。
 cellSize：单元格大小，形如(w,h)的元组，默认值(8,8)。
 nbins：直方图的条数，整数，默认值9。
 img：输入图像，单通道，数据类型CV_8U。
 winStride：窗口大小，可选项，必须是blockStride的整数倍。
 descriptors：HOG描述符，形为(lenHOG,)的Numpy 数组，数据类型CV_32F。

函数说明
⑴ 计算每个单元格cell的HOG：方向梯度的取值范围0～180度，等分为nbins个区间，单元格像素的梯度方向分配到nbins个扇形区间，累加每个区间内的像素数，得到nbins位的HOG向量。
⑵ 构造子块block的HOG：多个单元格cell组合为子块，子块的HOG描述符就是多个单元格HOG向量的串联，长度为nbins*blockSize/cellSize。
⑶ 整个检测窗口的HOG：子块block以步长blockStride在检测窗口内滑动，遍历检测窗口，检测窗口的HOG就是每个子块block的HOG的串联。
因此，检测窗口的HOG的向量维数是：

lenHOG = nbins * (blockSize[0]/cellSize[0]) * (blockSize[1]/cellSize[1])
* ((winSize[0]-blockSize[0])/blockStride[0] + 1)
* ((winSize[1]-blockSize[1])/blockStride[1] + 1)

注意问题

• ⑴ 函数cv.HOGDescriptor实例化HOGDescriptor类，定义一个HOGDescriptor类对象。成员函数hog.compute计算给定图像的HOG描述符。

# 构造 HOG 检测器
winSize = (40, 40)
blockSize = (20, 20)
blockStride = (10, 10)
cellSize = (10, 10)
nbins = 8
hog = cv.HOGDescriptor(winSize, blockSize, blockStride, cellSize, nbins)
# hog = cv.HOGDescriptor(_winSize=(40,40), _blockSize=(20,20), 
#      _blockStride=(10,10), _cellSize=(10,10), _nbins=8)
1
2
3
4
5
6
7
8
9

• ⑵ 检测窗口大小winSize是子块大小blockSize的整数倍，子块大小blockSize是单元格大小cellSize的整数倍，子块大小blockSize是滑动步长blockStride的整数倍。
• ⑶ 函数中方向梯度的取值范围是0～180度，而不是0～360度。
• ⑷ cv::HOGDescriptor类的功能丰富，参数和成员函数很多，例如可以实现尺度不变性检测。更多使用方法可以参见OpenCV官方文档 【链接1 】。

3. 例程：特征描述之HOG描述符

本例程示例HOG描述符的使用。为了便于解释HOG原理和绘图，例程中将检测窗口、子块和单元格设为相同的尺寸，实际应用时可以参考函数默认值来设置。

# 【1609】特征描述之 HOG 描述符
import cv2 as cv
import numpy as np
from matplotlib import pyplot as plt

def drawHOG(image, descriptors, cx, cy, rad):
    angles = np.arange(0, 180, 22.5).astype(np.float32)  # start, stop, step
    normGrad = descriptors/np.max(descriptors).astype(np.float32)
    gx, gy = cv.polarToCart(normGrad*rad, angles, angleInDegrees=True)
    for i in range(angles.shape[0]):
        px, py = int(cx+gx[i]), int(cy+gy[i])
        cv.arrowedLine(image, (cx,cy), (px, py), 0, tipLength=0.1)  # 黑色
    return image

if __name__ == '__main__':
    # (1) 读取样本图像，构造样本图像集合
    img = cv.imread("../images/Fig1101.png", flags=0)  # 灰度图像
    height, width, wCell, d = 200, 200, 20, 10
    img = cv.resize(img, (width, height))  # 调整为统一尺寸

    # (2) 构造 HOG 检测器
    winSize = (20, 20)
    blockSize = (20, 20)
    blockStride = (20, 20)
    cellSize = (20, 20)
    nbins = 8
    hog = cv.HOGDescriptor(winSize, blockSize, blockStride, cellSize, nbins)
    lenHOG = nbins * (blockSize[0]/cellSize[0]) * (blockSize[1]/cellSize[1]) \
            * ((winSize[0]-blockSize[0])/blockStride[0] + 1) \
            * ((winSize[1]-blockSize[1])/blockStride[1] + 1)
    print("length of descriptors:", lenHOG)

    # (3) 计算检测区域的 HOG 描述符
    xt, yt = 80, 80  # 检测区域位置
    cell = img[xt:xt+wCell, yt:yt+wCell]
    cellDes = hog.compute(cell)  # HOG 描述符，(8,)
    normGrad = cellDes/np.max(cellDes).astype(np.float32)
    print("shape of descriptors:{}".format(cellDes.shape))
    print(cellDes)

    # (4) 绘制方向梯度示意图
    imgGrad = cv.resize(cell, (wCell*10, wCell*10), interpolation=cv.INTER_AREA)
    Gx = cv.Sobel(img, cv.CV_32F, 1, 0, ksize=5)  # X 轴梯度 Gx
    Gy = cv.Sobel(img, cv.CV_32F, 0, 1, ksize=5)  # Y 轴梯度 Gy
    magG, angG = cv.cartToPolar(Gx, Gy, angleInDegrees=True)  # 极坐标求幅值与方向 (0~360)
    print(magG.min(), magG.max(), angG.min(), angG.max())
    angCell = angG[xt:xt+wCell, yt:yt+wCell]
    box = np.zeros((4, 2), np.int32)  # 计算旋转矩形的顶点, (4, 2)
    for i in range(wCell):
        for j in range(wCell):
            cx, cy = i*10+d, j*10+d
            rect = ((cx,cy), (8,1), angCell[i,j])  # 旋转矩形类
            box = np.int32(cv.boxPoints(rect))  # 计算旋转矩形的顶点, (4, 2)
            cv.drawContours(imgGrad, [box], 0, (0,0,0), -1)

    # (5) 绘制检测区域的方向梯度直方图
    cellHOG = np.ones((201,201), np.uint8)  # 白色
    cellHOG = drawHOG(cellHOG, cellDes, xt+d, yt+d, 40)

    # (6) 绘制图像的方向梯度直方图
    imgHOG = np.ones(img.shape, np.uint8)*255  # 白色
    for i in range(10):
        for j in range(10):
            xc, yc = 20*i, 20*j
            cell = img[xc:xc+wCell, yc:yc+wCell]
            descriptors = hog.compute(cell)  # HOG 描述符，(8,)
            imgHOG = drawHOG(imgHOG, descriptors, xc+d, yc+d, 8)
    imgWeight = cv.addWeighted(img, 0.5, imgHOG, 0.5, 0)

    plt.figure(figsize=(9, 6.2))
    plt.subplot(231), plt.title("1. Original")
    cv.rectangle(img, (xt,yt), (xt+wCell,yt+wCell), (0,0,0), 2)  # 绘制 block
    plt.axis('off'), plt.imshow(img, cmap='gray')
    plt.subplot(232), plt.title("2. Oriented gradient")
    angNorm = np.uint8(cv.normalize(angG, None, 0, 255, cv.NORM_MINMAX))
    plt.axis('off'), plt.imshow(angNorm, cmap='gray')
    plt.subplot(233), plt.title("3. Image with HOG")
    cv.rectangle(imgWeight, (xt,yt), (xt+wCell,yt+wCell), (0,0,0), 2)  # 绘制 block
    plt.axis('off'), plt.imshow(imgWeight, cmap='gray')
    plt.subplot(234), plt.title("4. Grad angle of cell")
    plt.axis('off'), plt.imshow(imgGrad, cmap='gray')
    plt.subplot(235), plt.title("5. HOG of cell")
    strAng = ("0", "22", "45", "67", "90", "112", "135", "157")
    plt.bar(strAng, cellDes*wCell*wCell)
    plt.subplot(236), plt.title("6. HOG diagram of cell")
    plt.axis('off'), plt.imshow(cellHOG, cmap='gray')
plt.tight_layout()
plt.show()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88

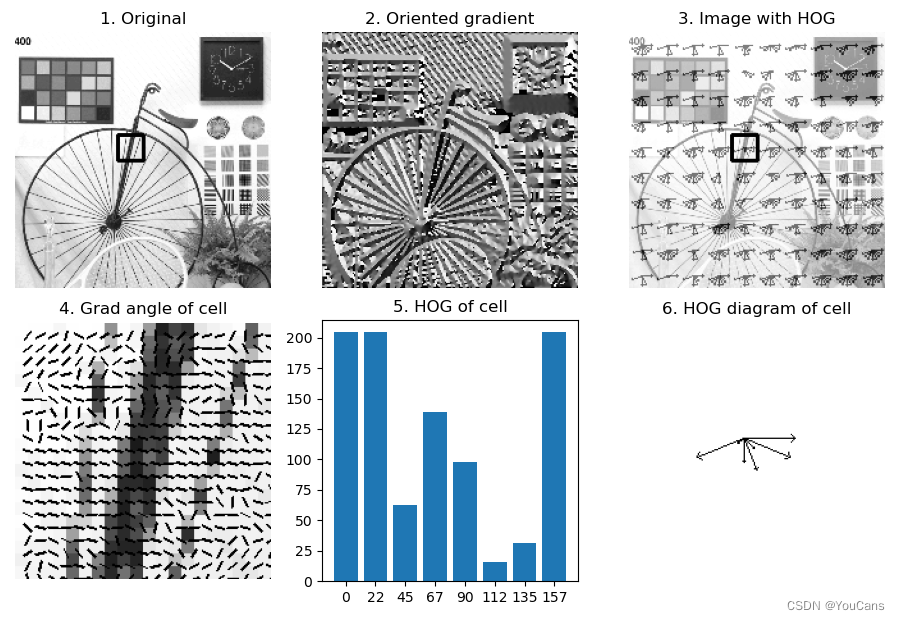
程序说明：

• ⑴ 子图1是原始图像，图中黑色方框是一个单元格cell。子图2是原始图像的梯度方向图，像素值的大小反映梯度方向的角度。
• ⑵ 子图4是子图1中方框位置单元格cell的梯度方向图，图中的线段表示像素点的梯度方向。注意例程中梯度方向的范围是0～180度。
• ⑶ 子图5是对子图4单元格中的所有像素点，按8个方向区间绘制的方向梯度直方图。子图6是子图5的单元格方向梯度直方图的空间矢量表示。
• ⑷ 子图3是整个图像的可视化方向梯度直方图.将图像划分为10*10个单元格，计算每个单元格的HOG，表示为如子图6的空间矢量形式。
• ⑸ 虽然例程给出了HOG处理过程和结果的各种图像，这是为了便于理解HOG的思路和计算步骤。在实际应用中，检测图像的HOG是维数为lenHOG的特征向量，而不是二维图像。

---

参考文献：Navneet Dalal, Bill Triggs. Histograms of oriented gradients for human detection. In Computer Vision and Pattern Recognition, 2005. CVPR 2005. IEEE Computer Society Conference on, volume 1, pages 886–893. IEEE, 2005.

【本节完】

版权声明：
youcans@xupt 原创作品，转载必须标注原文链接：(https://blog.csdn.net/youcans/article/details/127970587)
Copyright 2022 youcans, XUPT
Crated：2022-11-20