-
19182 石子合并(基础版)
题目
19182 石子合并(基础版)
时间限制:1000MS 代码长度限制:10KB
提交次数:0 通过次数:0题型: 编程题 语言: 不限定
Description
设有 N(N≤300) 堆石子排成一排,其编号为1,2,3,⋯,N。每堆石子有一定的质量 mi(mi≤1000)。
现在要将这N堆石子合并成为一堆。每次只能合并相邻的两堆,合并的代价为这两堆石子的质量之和,合并后与这两堆石子相邻的石子将和新堆相邻。
合并时由于选择的顺序不同,合并的总代价也不相同。试找出一种合理的方法,使总的代价最小,并输出最小代价。输入格式
第一行,一个整数 N。第二行,N 个整数 mi。
输出格式
输出仅一个整数,也就是最小代价。(题目确保答案在int范围)输入样例
4
2 5 3 1输出样例
22提示
区间动态规划。题解可参考 11078 不能移动的石子合并(优先做)代码
#include#include #include #include #define N 301 using namespace std; int s[N]; // (前缀和)s[i]表示前i个整数之和 int dp[N][N]; // dp[i][j]表示将第i个石头到第j个石头合并在一起的方案集合中的最小代价 int main() { memset(dp, 0x7f, sizeof(dp)); // 给dp每个位置设置最大值,因为后面要用min找最小代价 int n; cin >> n; s[0] = 0; for(int i = 1; i <= n; i++) { cin >> s[i]; s[i] += s[i - 1]; dp[i][i] = 0; // 自己和自己不用合并,代价是0 } for(int len = 2; len <= n; len++) // 合并长度范围 { for(int l = 1; l + len - 1 <= n; l++) // 合并集合的左边界 { int r = l + len - 1; // 合并集合的右边界 for(int mid = l; mid < r; mid++) // 将集合拆分成两部分 { dp[l][r] = min(dp[l][r], dp[l][mid] + dp[mid + 1][r] + s[r] - s[l - 1]); // 找到最小代价 } } } cout << dp[1][n]; return 0; } - 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
坑
- main函数外定义数组会自动初始化,而main函数内则不会
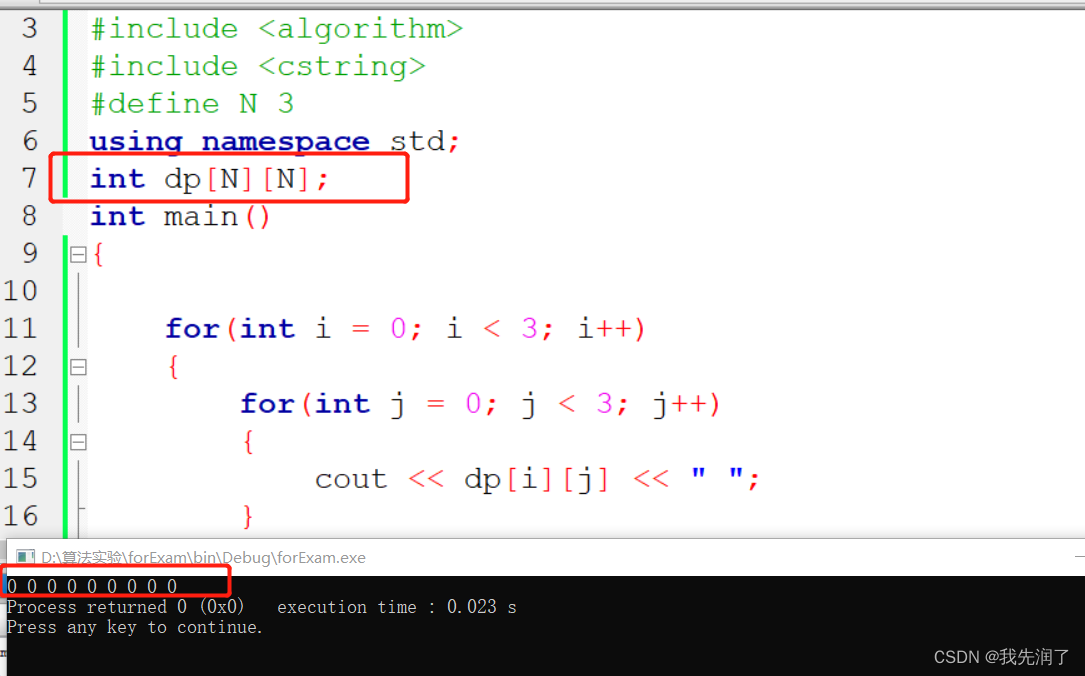
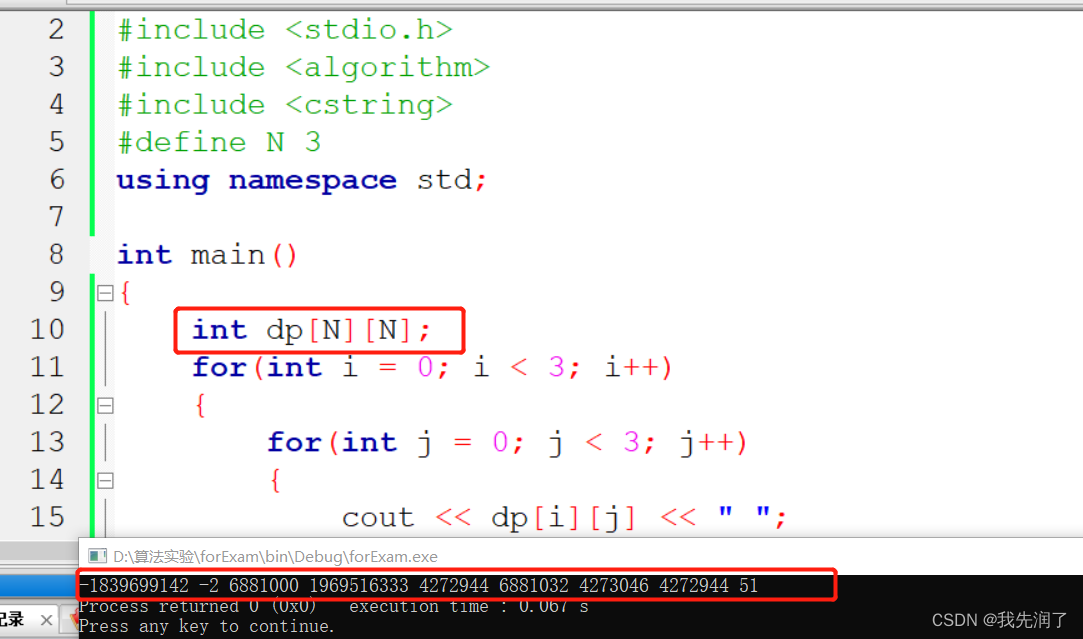
- memset填充的值以 int 形式传递,但是函数在填充内存块时是使用该值的无符号字符形式(char),只接受0x00-0xFF的赋值
C++中memset()函数的用法详解
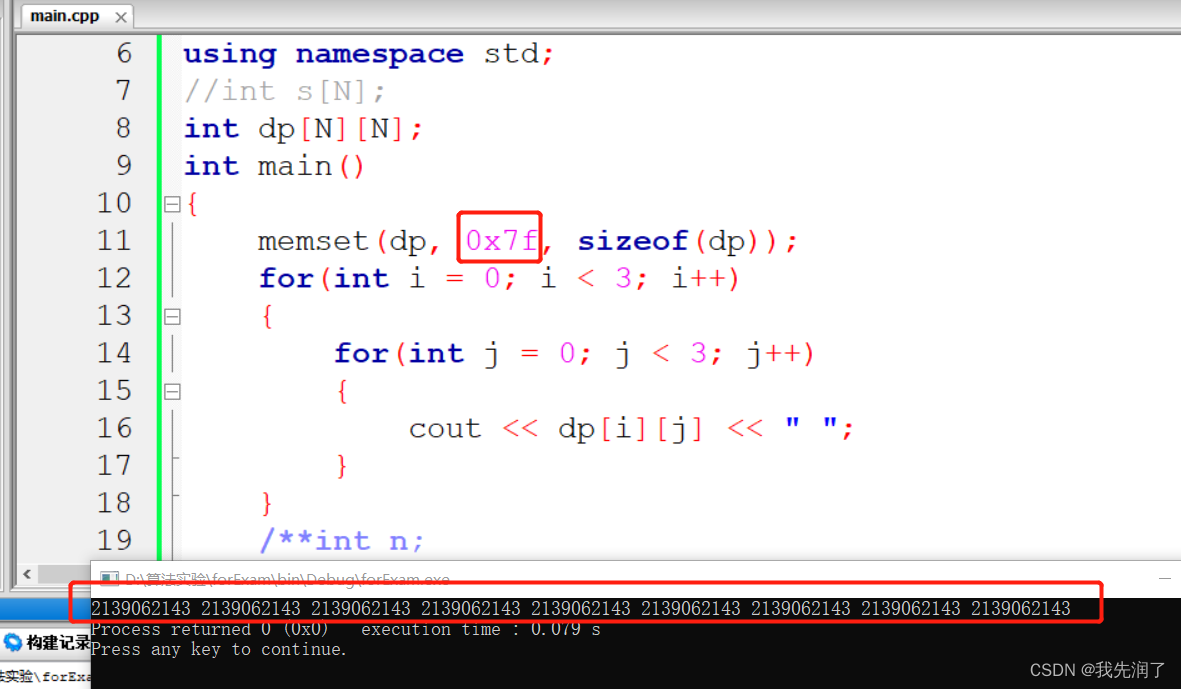
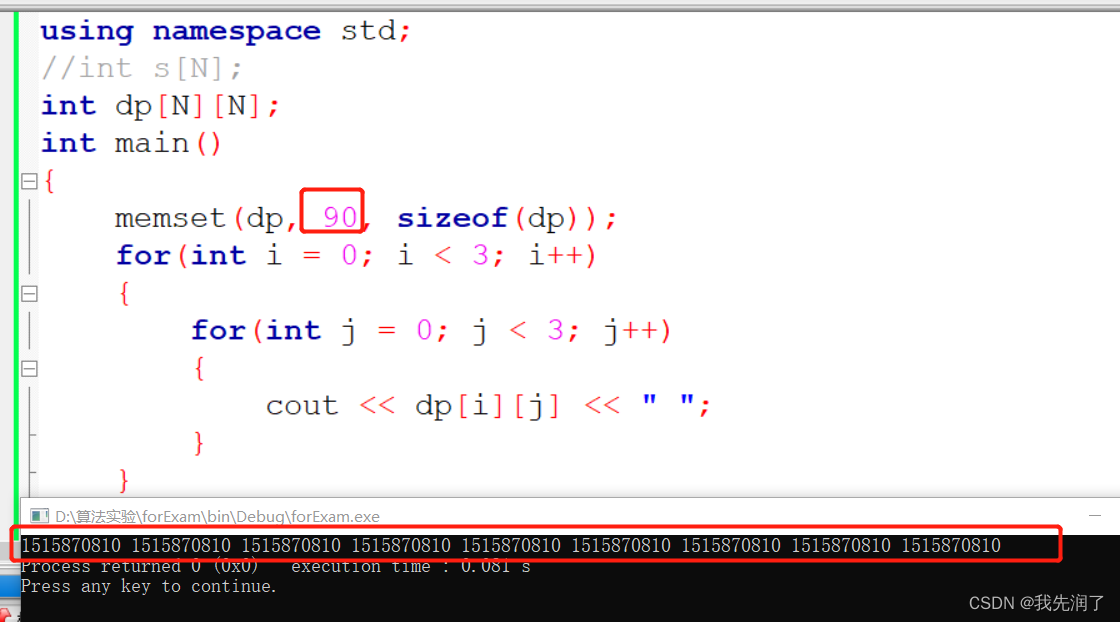
-
相关阅读:
C/C++ 数据结构 - 栈
Milvus 2.3.功能全面升级,核心组件再升级,超低延迟、高准确度、MMap一触开启数据处理量翻倍、支持GPU使用!
Linux下的第一个小程序——进度条
大模型会毁了初级程序员 —— 对话图灵奖得主 Joseph Sifakis | 新程序员
Mysql生产随笔
java 遍历文件夹目录树形结构并在控制台输出且保存到本地文件
Lodop 实现局域网打印
[MySQL] MySQL表的约束
Java实现单点登录(SSO)详解
数据结构·顺序表
- 原文地址:https://blog.csdn.net/weixin_54218079/article/details/127969565
