• PointNet 和 PointNet++ 作者讲座学习笔记

    文章目录

    前人的工作

    三维数据的表达形式

    • 点云：深度传感器扫描得到
    • Mesh：由三角面片或四边形面片组成，适合建模、渲染
    • 体素：把空间划分为三维网格，每个小的正方体组成
    • 多角度的图片：用于可视化
      在这里插入图片描述
      点云数据是一种非常适合三维场景理解算法的数据格式：
    1. 点云非常接近于原始的传感器数据。激光雷达扫描到的数据直接就是点云。可以做一种端到端的深度学习，能尽可能挖掘原始数据中的模式（信息）。
    2. 点云的表达形式非常简单

    在这里插入图片描述

    把点云转化为体素，再用3D CNN

    之前的工作
    在这里插入图片描述
    时空复杂度很高
    在这里插入图片描述
    在这里插入图片描述

    PointNet

    直接用点云
    端到端的学习
    在这里插入图片描述
    在这里插入图片描述

    两个挑战

    • 置换不变性
    • 旋转不变性
      在这里插入图片描述

    置换不变性

    输入是无序的，模型需要对 N ! N! N!个排列结果保持不变
    在这里插入图片描述
    解决置换不变性的方法：对称函数。
    因为对称函数跟排列是没有关系的
    在这里插入图片描述
    在神经网络中如何应用对称函数
    在这里插入图片描述
    对每一维取最大值，但是这样丢失了很多特征。
    可以先将数据升维，由于信息冗余，使得 m a x max max操作可以保留更多的点云数据。
    在这里插入图片描述
    一个原始的PointNet结构
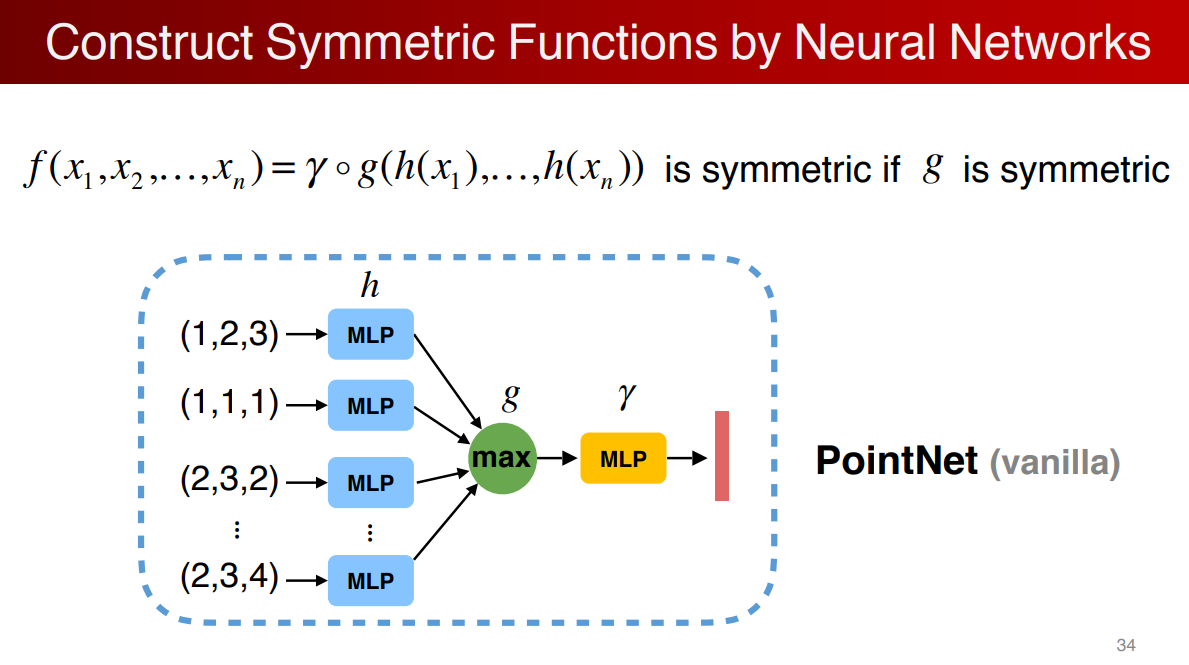
    在这里插入图片描述

    理论证明，PointNet可以逼近任意连续函数
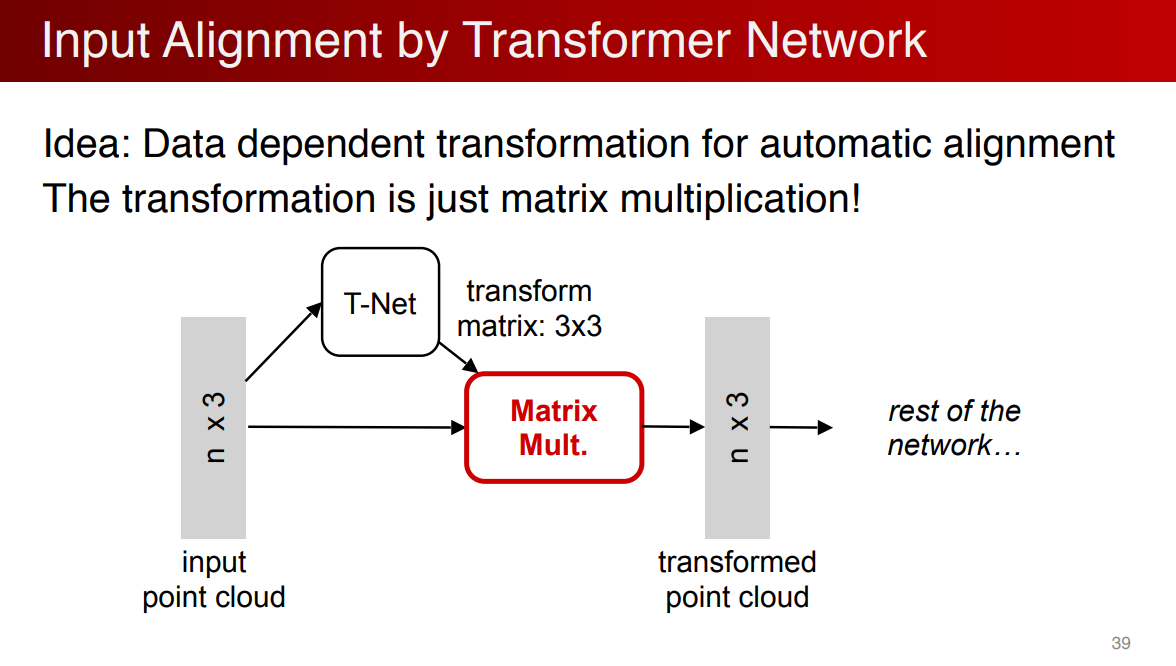
    在这里插入图片描述

    旋转不变性

    在这里插入图片描述
    使用Transformer Network对其输入
    在这里插入图片描述

    PointNet的分类网络

    在这里插入图片描述

    PointNet的分割网络

    在这里插入图片描述
    PointNet对数据丢失是鲁棒的
    在这里插入图片描述
    解释了为什么对点的丢失非常鲁棒，因为学习到了关键点
    在这里插入图片描述

    PointNet的限制

    要么是对一个点做操作，要么是对全局的点做操作，它没有局部的操作。

    在这里插入图片描述
    因为没有局部特征的学习，所以在分割精细的点上存在问题，在平移不变性上也有所缺陷。
    在这里插入图片描述

    PointNet++

    核心思想：在局部区域重复地迭代性地使用PointNet
    在这里插入图片描述

    • 实现了多级的特征学习
    • 因为在区域中，可以用局部坐标系，可以实现平移不变性
    • 由于在小区域内使用PointNet，保证了置换不变性

    多级点云特征学习

    用一个具体例子来理解多级点云特征学习
    在这里插入图片描述
    假设找到红点周围的小区域
    在这里插入图片描述
    因为不想受整体平移的影响，先把小区域的点转化到局部坐标系
    在这里插入图片描述
    对小区域使用PointNet提取局部特征
    在这里插入图片描述
    提取完特征得到一个新的点
    在这里插入图片描述
    这个点不仅有X，Y坐标，还有代表小区域几何形状的特征向量

    重复这个过程，得到一组新的点
    在这里插入图片描述
    这组点往往在数量上少于原先的点，但每个点代表了它周围几何区域的点。这组操作叫作点集提取。

    分类

    经过两层点集提取，再经过pooling，得到全局特征，然后做分类。
    在这里插入图片描述

    分割

    将全局特征再传递给原来的点上就可以实现分割。
    在这里插入图片描述

    小区域大小

    如何选择局部小区域的大小？
    类比卷积神经网络，在CNN中，小的kernel比较流行。
    在这里插入图片描述

    点云中常见的问题是采样不均匀，近的点非常密，远的点非常疏。一个极端的情况，小区域中只有一个点，那么学习到的特征会非常不稳定。

    在这里插入图片描述

    在这里插入图片描述
    通过对比实验，得到结论：在点云中，kernel太小的话会被采样率的不均匀所影响。

    针对这个问题，提出MSG和MRG。
    动机是，希望在密的地方相信这个特征；在疏的地方不相信这个特征，而是看更大的区域。
    在这里插入图片描述

    参考资料

    斯坦福大学在读博士生祁芮中台：点云上的深度学习及其在三维场景理解中的应用

  • 相关阅读:
    HTTP协议
    @postconstruct注解获取不到本身的bean
    STC8H开发(十五): GPIO驱动Ci24R1无线模块
    39+又是一篇惊鸿巨作，教你如何打造高分SCI文章
    当新手小白有了一块【香橙派OrangePi AIpro】.Demo
    Golang标准包time总结
    LLM在text2sql上的应用
    QT事件系统_lineEdit输入信息触发事件方法
    HPCPlus怎么使用
    零基础转行，入职军工类测试方向，月薪10K | 既然选择了，就要全力以赴
  • 原文地址：https://blog.csdn.net/m0_46283220/article/details/127938081