基于小波域的隐马尔可夫树模型的图像去噪方法的matlab实现代码

目录

1.算法概述

2.仿真效果预览

3.MATLAB部分代码预览

4.完整MATLAB程序

---

1.算法概述

        为适应图像的空域非平稳变化, 提出了一种基于小波域分类隐马尔可夫树(CHMT)模型的图像去噪方法.该模型中,图像在每一尺度每一子带的小波系数均被分成C组以突出其空域非平稳变化 的特征,这样原来的一棵小波四叉树被分成了C棵具有不同HMT参数的小波四叉树,再经过合理的初始化和期望最大化(EM)算法训练参数,反变换恢复.实验 结果表明,与已有方法相比,该方法在不增加计算量的前提下,明显改善了所恢复图像的质量(PSNR).

        采用基于小波域隐马尔可夫树模型(HMT)对纹理进行分析,并有机地结合遥感图像的要求和特点进行深入研究。由于小波系数不满足高斯分布,在同尺度内和尺度间都表现为一种潜在的依赖关系,所以小波域HMT模型较准确地揭示了小波系数间的这些依赖关系。

        在马尔可夫模型中，每个状态代表了一个可观察的事件，所以，马尔可夫模型有时又称作可视马尔可夫模型（visibleMarkovmodel，VMM），这在某种程度上限制了模型的适应性。

      对于盲人来说也许不能够直接获取到天气的观察情况，但是他可以通过触摸树叶通过树叶的干燥程度判断天气的状态。于是天气就是一个隐藏的状态，树叶的干燥程度是一个可观察的状态，于是我们就有了两组状态，一个是不可观察、隐藏的状态（天气），一个是可观察的状态（树叶），我们希望设计一种算法，在不能够直接观察天气的情况下，通过树叶和马尔可夫假设来预测天气。

以此为例，一个一阶的马尔可夫过程描述：

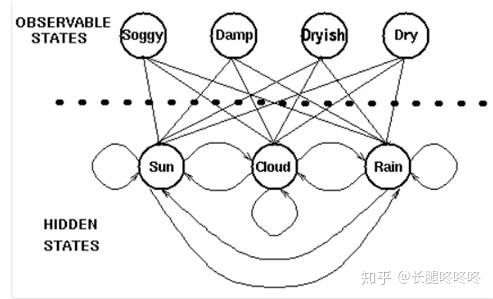
       在隐马尔可夫模型（HMM）中，我们不知道模型具体的状态序列，只知道状态转移的概率，即模型的状态转换过程是不可观察的。

        隐马尔可夫模型是马尔可夫链的一种，它的状态不能直接观察到，但能通过观测向量序列观察到，每个观测向量都是通过某些概率密度分布表现为各种状态，每一个观测向量是由一个具有相应概率密度分布的状态序列产生。所以，隐马尔可夫模型是一个双重随机过程----具有一定状态数的隐马尔可夫链和显示随机函数集。自20世纪80年代以来，HMM被应用于语音识别，取得重大成功。到了90年代，HMM还被引入计算机文字识别和移动通信核心技术“多用户的检测”。HMM在生物信息科学、故障诊断等领域也开始得到应用。

2.仿真效果预览

matlab2022a仿真

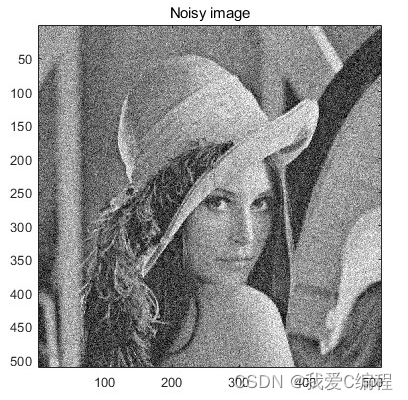
3.MATLAB部分代码预览

clc;
clear;
close all;
warning off;
addpath(genpath(pwd));
 
 
load lena;
 
sigma = 0.1; %noise standard deviation
hh = daubcqf(4); %wavelet filter
 
x = lena + sigma*randn(size(lena));
disp(['PSNR of noisy image is ' num2str(psnr(lena,x)) 'dB']);
y=hdenoise(x,hh);
disp(['PSNR of denoised image is ' num2str(psnr(lena,y)) 'dB']);
figure(1);
image(x*255+1);
colormap(gray(256));
axis square;
title('Noisy image');
figure(2);
image(y*255+1);
colormap(gray(256));
axis square;
title('Denoised image');
A_013

4.完整MATLAB程序

matlab源码说明_我爱C编程的博客-CSDN博客

V