-
AST 初探深浅,代码还能这样玩?
AST 听起来好像是个很新的东西,那么具体有什么用,好不好用就在这篇文章中找到答案吧~
我们简单将这个词拆分
抽象、语法、树,如果我们能够顺利将这个词拆分,那么我们也就掌握了其核心所在- 抽象:抽象的反义词是具象,也就说明抽象的事物关注点不在于细节,而在于整体
- 语法:语法一组词法的表达式,具备某种指定的规则,具有某种特定的意义,比如 1+1
- 树:树是一种一对多的结构,通过根节点往下递生,可以存在多个子树,当然这不是我们这篇讨论的主题,但却是重点
我们接下来通过几个例子更加清楚了解一下什么是树
一、什么是树?
1)算数表达式
5 * 4 / 2 + 3 * 6 这是一个简单的算法运算,但是如果我们要通过树形的方式表达它的话,结果可能是以下这样:

我们通过分析这张树形图,我们可以发现有哪几个结构 ?
- 一部分是数字:
5,4,2,3,6 - 一部分是操作符:
*, /, +, *
我们从中抽取出了
+符号,并将其作为该树的根节点,这个时候又可以分为左右两个子树,我们从中提取出一棵子树来看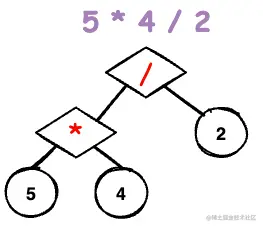
观察发现子树又变成了一棵树,那么可以得出一个结论:任何一棵子树都可以独立成为一棵完整的树,多个子树可以组合成一棵完整的树。至此,我们就完成了一棵树的定义,接下来我们再看一个其他例子
2)XML 文件
XML文件也是我们日常中比较常用到的文件结构
- <person>
- <name>
- 张三
- </name>
- <label>
- 法外狂徒
- </label>
- </person>
- 复制代码
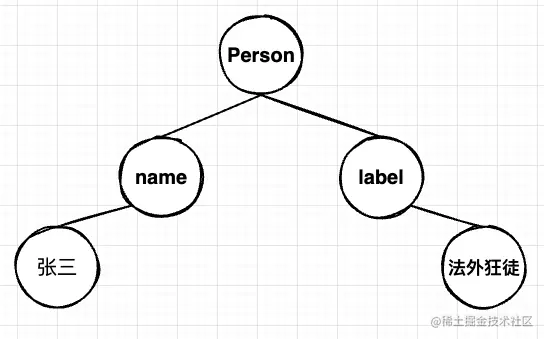
我们将文件结构转成属性结构后,就可以很直观的看出数据层级与内容
二、树的转换
树的有点是很直观,可以直接看出数据层级与内容,但是我们平时操作的时候只能是操作客观上的树形结构,而不是以上主观的树形结构。因此当我们得到上述树形结构后,我们就需要对该树进行扁平化操作,那问题来了,如何扁平化呢?
我们一样拿上述算数运算为例

红色的框框代表一棵树,而绿色和黄色框框则表示该树的两棵子树,当然
5 * 4当然也可以框起来作为绿色框的子树。这个时候,聪明的小伙伴们看到这些树有没有什么发现,比如每棵树表示什么?
我们可以发现每棵树似乎都表示着一个算数运算
1)规则定义
转换需要建立在一定的规则基础上
我们需要先定义下规则,如果遇到一个运算,我们就以
BinaryExpression来表示,而 运算 中的结构自然就包含着 字符 和 运算符 ,比如5 * 4这是一个运算,我们将整体标识为一个BinaryExpression。而这个运算中存在三个元素,分别是:
5, 4, *。那么其中5和4我们就可以称之为 字符,*可以称之为 运算符。由此我们可以再定一个规则,字符 的类型我们可以用Identifier来标识,运算符 的类型我们就以Operator来表示。到这步我们就已经简单地定义好了一个 规则,接下来我们要做的事情就是利用我们的规则将上述树形结构扁平化
2)小试牛刀

-
相关阅读:
数据库 与 数据仓库
SpringBoot+Vue项目疫苗预约管理系统
Win11怎么重装显卡驱动程序?Win11显卡驱动怎么卸载重装?
java虚拟机详解篇六(类的加载机制)
使用扩展运算符(...)合并数组
关于2023届互联网秋招,我想简单说两句
react-router-dom使用指南(最新V6)
命名实体识别
利用回溯解决子集II遇到的二维数组去重问题
C++语言GDAL批量裁剪多波段栅格图像:基于像元个数裁剪
- 原文地址:https://blog.csdn.net/m0_74931226/article/details/127961651