PID算法及其实现

PID算法

算法简介

PID即：Proportional（比例）、Integral（积分）、Differential（微分）的缩写。顾名思义，PID控制算法是结合比例、积分和微分三种环节于一体的控制算法。从20世纪30至40年代出现至今，PID算法不仅在工业流程控制中被广泛应用，小到元件温度控制，大到汽车定位巡航等。现在在互联网广告中也有不少应用PID算法的地方

算法应用

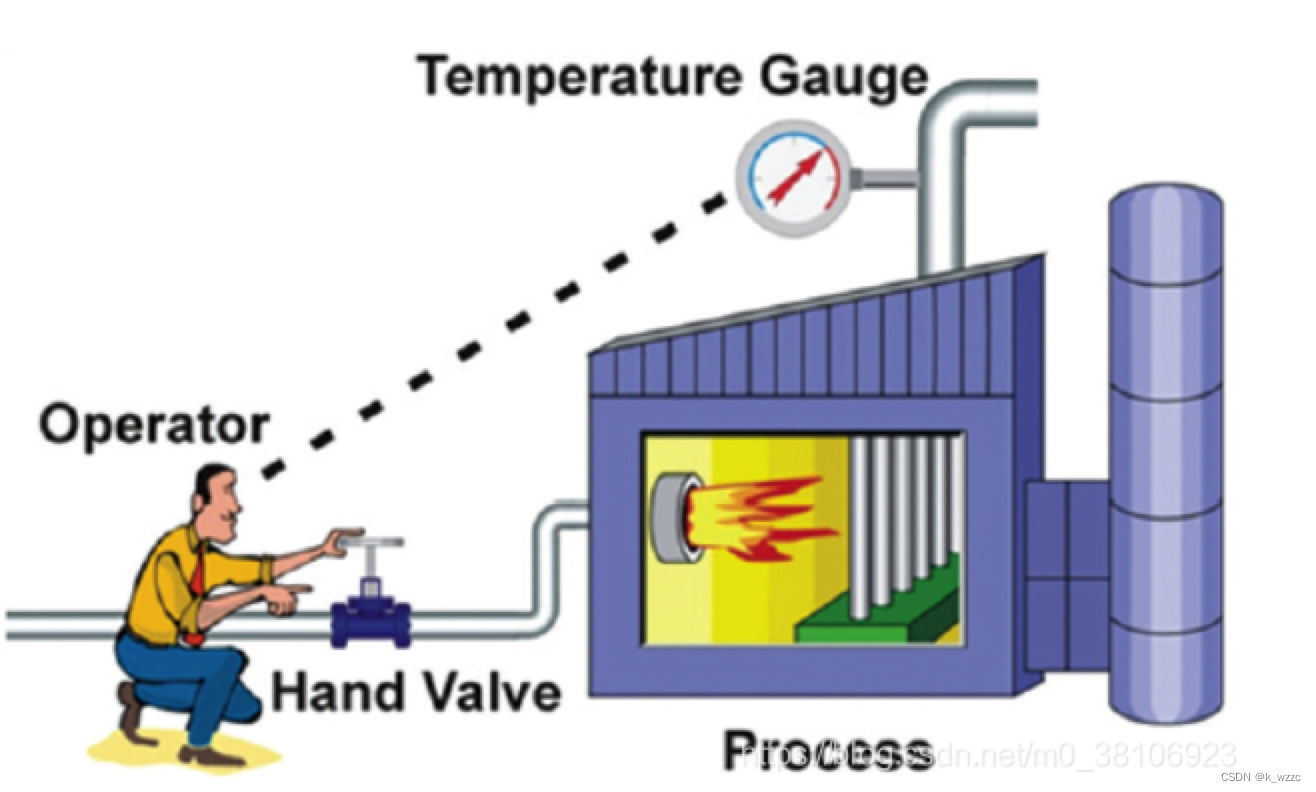
PID算法原理

PID算法公式：

u(t) = K_p(e(t) + \frac{1}{T_t}\int^t_0 e(t){\rm d}t  + T_d\frac{de(t)}{dt})
1

• Tt ——积分时间常数 ;
• Td ——微分时间常数；
• u(t)——PID控制器的输出信号；
• e(t)——给定值r(t)与测量值之差。

经过变换可得

u(t) = K_pe(t) + K_i\int^t_0 e(t){\rm d}t  + Kd\frac{de(t)}{dt})

1
2

上面的公式每一部分都对应一个控制算法（比例、积分、微分）

常规的模拟PID控制系统原理框图如下所示：
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-jqF6H2CW-1668959786948)(https://note.youdao.com/yws/res/13206/AE61C125214849BE8040D3B8B58B50BF)]

PID算法通俗易懂的例子可以参看以下两篇文章：

https://bbs.huaweicloud.com/blogs/229961
https://zhuanlan.zhihu.com/p/39573490

PID 算法分类

• 位置式：下一步去哪儿，直接给出变化到的位置
• 增量式：下一步要变化多少到达目标，给出变化量
  增量式的算法，这两者只是在算法的实现上的存在差异，本质的控制上对于系统控制的影响还是相同

增量式PID算法公式如下：

u(t) = K_p(e(t)-e(t-1) )+ K_ie(t)  + K_d(e(t)-2e(t-1)+e(t-2))

1
2

代码实现

位置式PID

/**
 * 位置式PID
 *
 * @param dt           采样周期
 * @param kp           比例增益
 * @param ki           积分增益
 * @param kd           微分增益
 * @param integalError 累积误差
 * @param preError     上次误差
 */
case class PositionPID(
                        dt: Double, // 采样周期
                        kp: Double, // 比例增益
                        ki: Double, // 积分增益
                        kd: Double, // 微分增益
                        var integalError: Double = 0, // 累积误差
                        var preError: Double = 0 // 上次误差
                      ) {

  def calculate(targetValue: Double, processValue: Double): Double = {

    //  误差  error =目标值-过程值
    val error = targetValue - processValue
    //    kp * e(t)
    val p = kp * error
    //  ki* ∑e(t)*δt
    val i = ki * (error + integalError) * dt
    integalError += error
    //    kd * (e(t)-e(t-1))/δt
    val d = kd * (error - preError) / dt

    //   新的过程值   
    val out = p + i + d
    preError = error

    out

  }

}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41

增量式PID

/**
 *
 * @param dt           采样周期
 * @param kp           比例增益
 * @param ki           积分增益
 * @param kd           微分增益
 * @param currentError 当前误差
 * @param preError     上次误差
 * @param preError2    上上次误差
 * @param preOutput    上次输出值
 */
case class IncrementPID(
                         dt: Double, // 采样周期
                         kp: Double, // 比例增益
                         ki: Double, // 积分增益
                         kd: Double, // 微分增益
                         var currentError: Double = 0, // 当前误差
                         var preError: Double = 0, //上次误差
                         var preError2: Double = 0, // 上上次误差
                         var preOutput: Double = 0 // 上次输出值
                       ) {

  def calculate(targetValue: Double, processValue: Double): Double = {

    //  误差  error =目标值-过程值
    val error = targetValue - processValue

    //    比例调节
    val p = kp * (error - preError)
    //    积分调节
    val i = ki * error
    //    微分调节
    val d = kd * (error - 2 * preError + preError2)

    val out = p + i + d + preOutput

    preError2 = preError
    preError = error
    preOutput = out

    out

  }

}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45

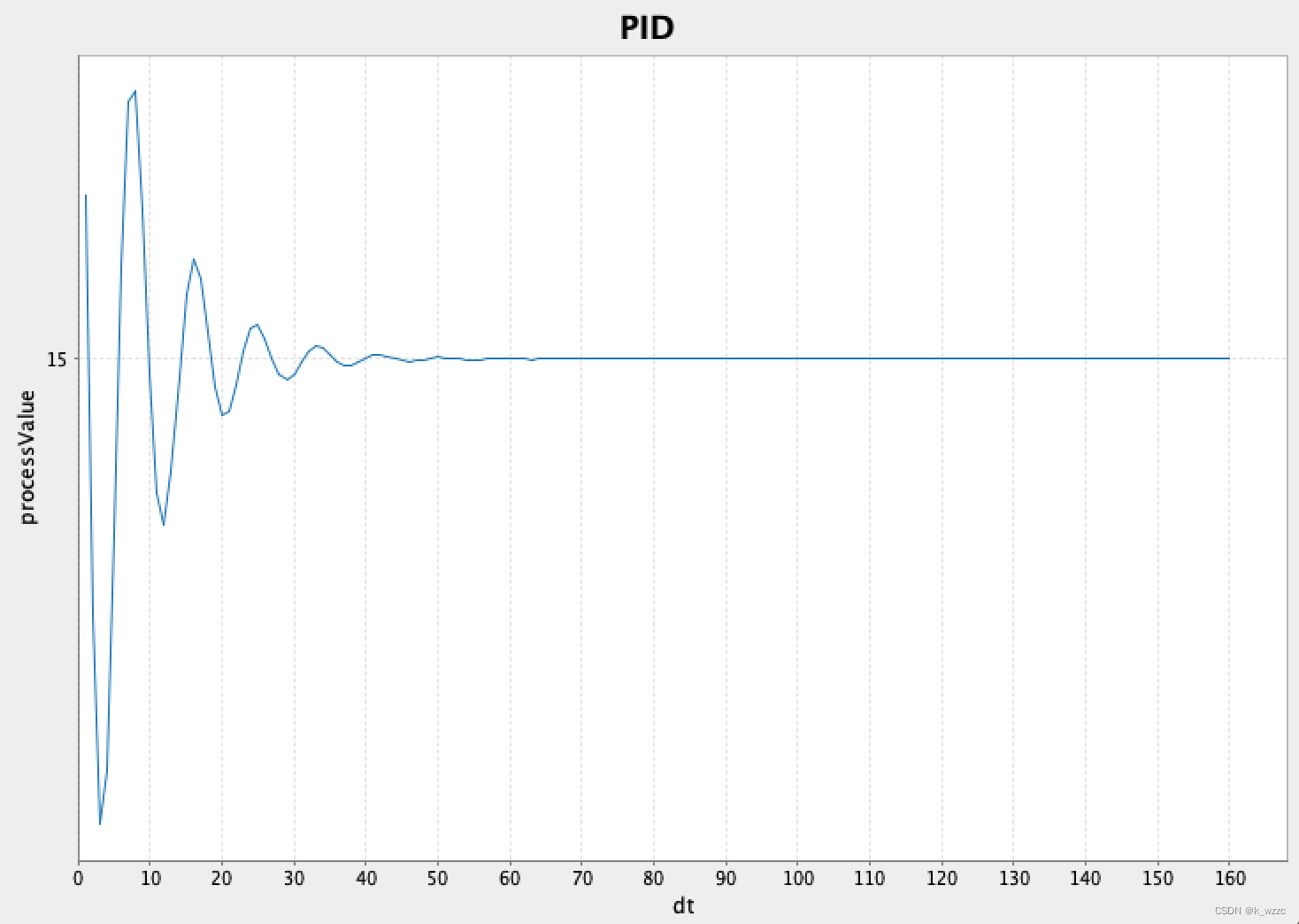
结果测试

def main(args: Array[String]): Unit = {

    val ppid = PositionPID(0.1, 0.1, 0.5, 0.01)
    var processValue = 0.0
    val targetValue = 15.0
    val dts = 1 to 160

    for (i <- dts) {
      val t = ppid.calculate(targetValue, processValue)
      processValue += t

      println(s"processValue:${processValue},t:${t}")
    }

    val ipid = IncrementPID(0.1, 0.2, 0.5, 0.05)

    val ps = new ListBuffer[Double]()

    for (i <- dts) {
      val t = ipid.calculate(targetValue, processValue)
      processValue += t
      ps.append(processValue)
      println(s"processValue:${processValue},t:${t}")
    }

    val f: Figure = Figure()
    val p: Plot = f.subplot(0)

    val psv = new DenseVector(ps.toArray)
    val xlable = new DenseVector(dts.map(_.toDouble).toArray)
    p += plot(xlable, psv)

    p.xlabel = "dt"
    p.ylabel = "processValue"
    p.title = "PID"

    f.saveas("/Desktoplines.png")

  }

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40

PID控制过程

参考资料

https://zhuanlan.zhihu.com/p/39573490

https://codeantenna.com/a/DcTWiCGMll

https://bbs.huaweicloud.com/blogs/229961

https://mp.weixin.qq.com/s?__biz=Mzg5MDU1OTgzMw==&mid=2247485702&idx=1&sn=b5dd06e736297cdef6fc778b88cdea31&source=41#wechat_redirect