计算机视觉算法——基于Transformer的语义分割（SETR / Segmenter / SegFormer）

之前我有对语义分割的方向进行一个简单总结：计算机视觉算法——语义分割网络总结，在全卷积网络提出，语义分割的框架大都是基于Encoder-Decoder的模式，其中Encoder用于压缩原始输入图像的分辨率并逐步提取抽象的语义特征，而Decoder主要将编码器所提取的语义特征进行上采样以进行像素级的预测。在这样的模式下，语义分割性能的好坏取决于网络感受野的大小，然而：

1. 研究表明，网络的实际感受野的大小要小于其理论感受野；
2. 感受野的增大往往意味着参数量的增加；
3. 过多的下采样会导致小目标的细节信息丢失；

因此，全卷积网络中的有效感受野是有限的，进而也就限制了网络性能的进一步提升。而Transformer的能够保持输入和输出空间的分辨率不变，并能够有效捕捉全局的上下文信息，将其应用到语义分割中必然也会带来相当的进步。Transfomer在图像分类和语义分割中应用之前都有总结过，感兴趣的读者可以参考：
计算机视觉算法——Vision Transformer / Swin Transformer
计算机视觉算法——基于Transformer的目标检测（DETR / Deformable DETR / DETR 3D）
下面我就对SETR、SegFormer、Segmenter进行一个简单的对比学习。

1. SETR

SETR发表于2021年CVRP，原论文名为《Rethinking Semantic Segmentation from a Sequence-to-Sequence Perspective with Transformers》，是第一篇基于Transfomer做语义分割的模型。

1.1 网络结构及特点

SETR的网络结构如下：

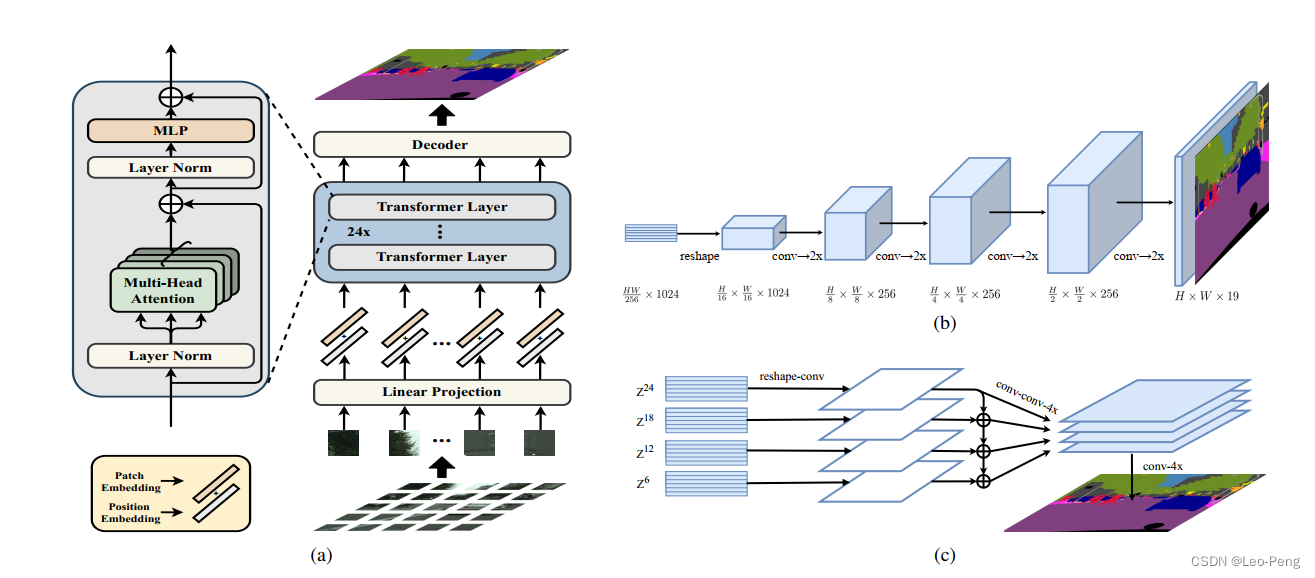
其中图（a）是整体的网路结构，图（b）和图（c）是两种不同的Decoder方式。

我们首先来看下整体的网络结构，SERT从输入部分到Encoder和ViT是接近的，先将$H\times W$图像按照$16\times 16$的大小划分为图像块，然后通过$1024$个$16\times 16$的卷积和转化为$H\times W/256$个长度为$1024$的Patch Embedding，再加上Positional Embedding后就融入有Multi Head Attention叠加起来的Encoder部分。详细的结构分析读者可以参考计算机视觉算法——Vision Transformer / Swin Transformer，这里我们来重点介绍下Decoder部分。

1.1.1 Decoder

SETR的论文中一共对比了三种Decoder模式：

1. 第一种是Naive Upsampling，具体做法$H\times W/256$个$1024$维的输出结果Reshape成$H/16\times W/16\times 1024$，然后通过两个$1\times 1$的卷积将特征变成$H/16\times W/16\times C$，其中$C$就是分类的大小，然后再将$H/16\times W/16\times C$通过双线性插值直接Upsample到原分辨率的大小且Cross Entropy损失。
2. 第二种是Progressive Upsampling，也就是上图中的图（b），为了避免引入噪声和边缘锯齿状，通过4次2倍的上采样逐步恢复尺寸。
3. 第三种是Multi-Level Feature Aggregation，也就是上图中的图（c），具体是从Eoncder中每隔6层抽取一个特征，然后Reshape成$H/16\times W/16\times 1024$大小，分别一个$1\times 1+3\times 3+3\times 3$的三层卷积网络，其中第一层和第三层会将通道数减少为原来的一半，输出$H/16\times W/16\times 256$，再通过双线性插值进行4倍的上采样得到$H/4\times W/4\times 256$。这四个$H/4\times W/4\times 256$的Feature接着按照自顶上下的方进行融合，顶层的特征和三个融合的特征进行Concat得到$H/4\times W/4\times 1024$的大小，最后再通过4倍上采样和卷积得到最后的$H\times W\times C$的特征图。

1.2 实验

首先是SETR于SoTA的方法的性能比较，在Cityscapes数据集上的结果如下：

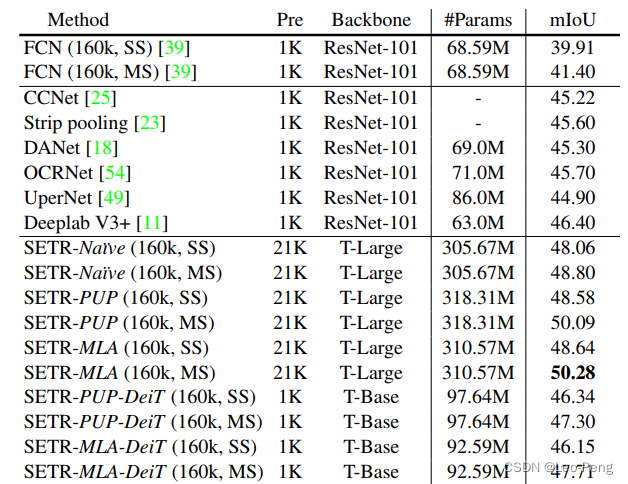
可以看到SETR在mIoU上确实有较大的提升，但是参数量也大了不少，同时作者在比较了不同Decode带来的性能变化，如下：

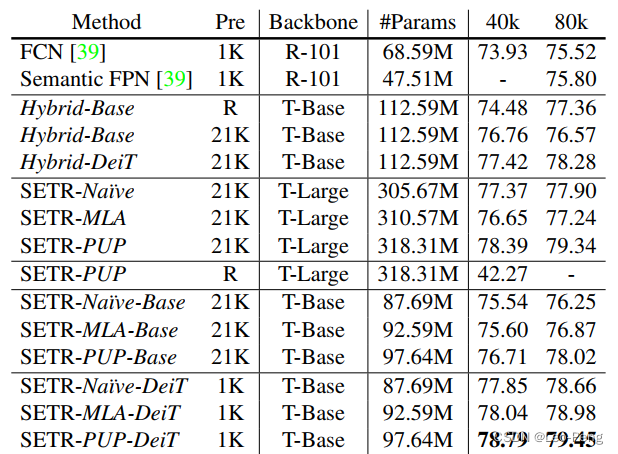
其中BackBone中的"T-Base"和"T-Large"分别指的是12层和24层Multi Head Self Attention。总的来说，SETR的思路还是比较直接的，说明了从用Transformer来做分割这条路是可以走通的，下面我们接着看看其他方法是如何在此基础上进行改进的。

2. Segmenter

Segmenter发表于2021年ICCV，原论文名为《Segmenter: Transformer for Semantic Segmentation》，其性能相对SETR要稍微好些。

2.1 网络结构及特点

Segmenter的网路结构如下图所示：

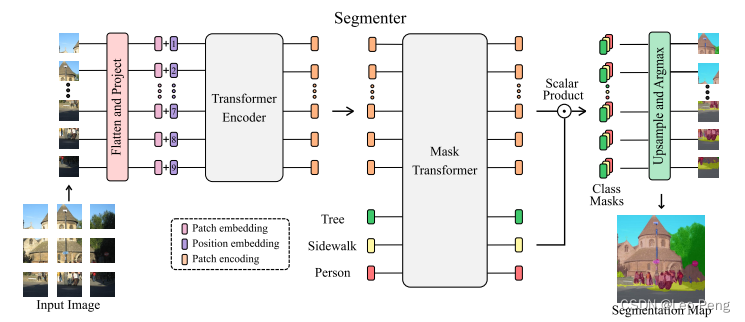
Segmenter的Encoder部分和SETR一致，都是远远本本地使用的ViT的Encoder，而Decoder相对SETR的直接使用MLP结合上采样作为Decoder，采用的是类似DETR的query的方法，具体我们来看下：

2.1.1 Decoder

Segmenter的Encoder输出的为Patch Embedding ${\mathbf{z}}_{\mathbf{L}}\in {\mathbb{R}}^{N\times D}$，其中$N$为Patch数量，$D$为Embedding的长度。而在Decoder中，输入中加入了Class Embedding $\mathbf{cls}={\mathbf{z}}_{\mathrm{lin}}\in {\mathbb{R}}^{N\times K}$，其中$K$为输出类别数量。在Decoder中，Patch Embedding和Class Embedding会经过若干个Attention Layer，最后通过点乘输出一个维度为$K\times N$的Feature：$$\mathrm{Masks}\left({\mathbf{z}}_{\mathbf{M}}^{\prime },\mathbf{c}\right)={\mathbf{z}}_{\mathbf{M}}^{\prime }{\mathbf{c}}^T$$该Feature最后经过Bilinearly Upsample以及最后Softmax得到最后的输出特征图，下面这个图说明了Class Embedding和最后输出的Segmentation map的关系：

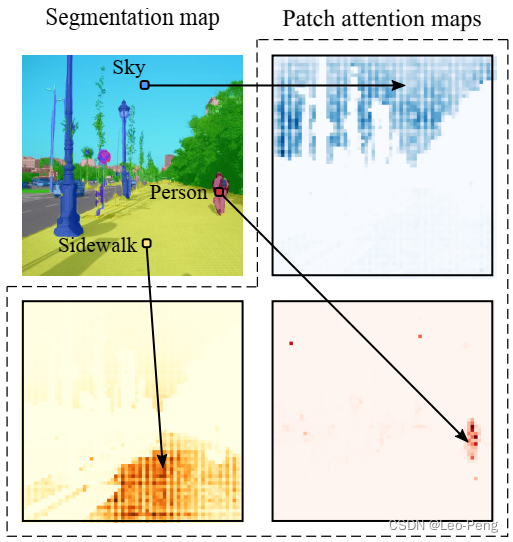
2.2 实验

首先作者比较了不同Patch大小的分割结果：

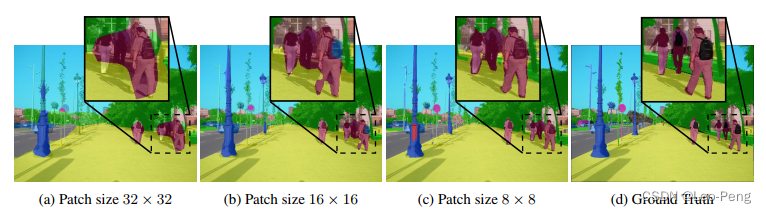
可以看到，要想起到较好的分割效果还是要将Patch尺寸取得比较小，对于ViT的Encoder来说，这个计算量是呈平方上升的，其次论文中有对比该方法和其他SoTA方法的结果：

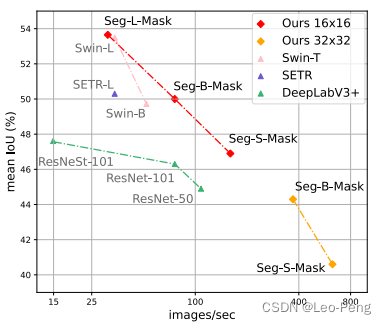
可以看到，相同计算效率下，Segmenter相对有SETR有些许提升，这也应该是得益于Segmenter的Decoder中更充分地利用到了注意力机制。

3. SegFormer

SegFormer发表于2021年NeurIPS，原论文名为《SegFormer: Simple and Efficient Design for Semantic Segmentation with Transformers》，论文中作者首先分析了SETR的不足之处：

1. 采用ViT-Large作为BackBone，其参数和计算量都是非常大，移动端模型无法承受；
2. 由于全程只能输出固定低分辨率的Feature，因此其实并不适合用来做语义分割，尤其是对轮廓细节要求比较精细的场景；
3. 一旦增大输入图片或者缩小Patch，计算量都会平方级上升；
4. 使用固定分辨率的Positional Embedding，但是语义分割的模型在测试或者使用时图像分辨率往往都不是固定的，遇到这种情况要么对Positional Embedding进行双线性插值损失性能，要么使用固定分辨率做滑动窗口。

针对这些问题，作者重新设计了Transformer Encoder和MLP Decoder，中间用到很多方法也是我之前没有接触到的，具体如下：

3.1 网络结构及特点

SegFormer的网络结构如下图所示：

从整体上看，Segformer的结构还是由Encoder和Decoder两部分组成的，但是图中出现了很多没有见过名词，例如Overlap Patch Embedding、Efficient Self-Attention、Mix-FFN等等，下面就一次对这些模块进行介绍：

3.1.1 Overlap Patch Merging

Segformer中的Patch Merging和Swin Transformer中Patch Merging目的是相同的，都是为了降低特征图，但是操作不一样。这里的Overlap Patch Merging要简单一些，Overlap Patch Merging本质就是一个Stride不为1的卷积模块，所谓Overlap也很好理解，当卷积的Stride小于Kernel Size时，那么Merging的特征相邻区域是具备Overlap信息的，这样的好处防止丢失局部连续性。如下：

class OverlapPatchEmbed(nn.Module):
    """ Image to Patch Embedding
    """

    def __init__(self, img_size=224, patch_size=7, stride=4, in_chans=3, embed_dim=768):
        super().__init__()
        img_size = to_2tuple(img_size)
        patch_size = to_2tuple(patch_size)

        self.img_size = img_size
        self.patch_size = patch_size
        self.H, self.W = img_size[0] // patch_size[0], img_size[1] // patch_size[1]
        self.num_patches = self.H * self.W
        self.proj = nn.Conv2d(in_chans, embed_dim, kernel_size=patch_size, stride=stride,
                              padding=(patch_size[0] // 2, patch_size[1] // 2))
        self.norm = nn.LayerNorm(embed_dim)

        self.apply(self._init_weights)

    def _init_weights(self, m):
        if isinstance(m, nn.Linear):
            trunc_normal_(m.weight, std=.02)
            if isinstance(m, nn.Linear) and m.bias is not None:
                nn.init.constant_(m.bias, 0)
        elif isinstance(m, nn.LayerNorm):
            nn.init.constant_(m.bias, 0)
            nn.init.constant_(m.weight, 1.0)
        elif isinstance(m, nn.Conv2d):
            fan_out = m.kernel_size[0] * m.kernel_size[1] * m.out_channels
            fan_out //= m.groups
            m.weight.data.normal_(0, math.sqrt(2.0 / fan_out))
            if m.bias is not None:
                m.bias.data.zero_()

    def forward(self, x):
        x = self.proj(x)
        _, _, H, W = x.shape
        x = x.flatten(2).transpose(1, 2)
        x = self.norm(x)

        return x, H, 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41

不同Block的Overlap Patch Embedding的定义如下：

self.patch_embed1 = OverlapPatchEmbed(img_size=img_size, patch_size=7, stride=4, in_chans=in_chans,
                                      embed_dim=embed_dims[0])
self.patch_embed2 = OverlapPatchEmbed(img_size=img_size // 4, patch_size=3, stride=2, in_chans=embed_dims[0],
                                      embed_dim=embed_dims[1])
self.patch_embed3 = OverlapPatchEmbed(img_size=img_size // 8, patch_size=3, stride=2, in_chans=embed_dims[1],
                                      embed_dim=embed_dims[2])
self.patch_embed4 = OverlapPatchEmbed(img_size=img_size // 16, patch_size=3, stride=2, in_chans=embed_dims[2],
                                      embed_dim=embed_dims[3])
1
2
3
4
5
6
7
8

可以看到第一个Block的Patch Merging模块Kernel Size大小为7，Stride为3，Padding为3，而后三个Patch Merging模块Kernel Size大小为3，Stride为2，Padding为1，这样的话就分别得到了分辨率分别为$\frac{1}{4},\frac{1}{8},\frac{1}{16},\frac{1}{32}$的特征图，而这些不同分辨率的Feature map会在后后面的Decoder中进行融合。

3.1.2 Efficient Self Attention

Efficient Self Attention的想法来自于《 Pyramid vision transformer: A versatile backbone for dense prediction without convolutions》，主要的目的是为了减小Self Attention的计算量，而Self Attention模块也正是整个Encoder中计算量占据比重最大的一块。

原始的Self Attention的公式为：$$\mathrm{Attention}(Q,K,V)=\mathrm{Softmax}\left(\frac{Q{K}^{\top }}{\sqrt{d_{head}}}\right)V$$其中$Q,K,V$的维度均为$N\times C$，而$N=H\times W$为整个输入序列的长度，该过程的计算量是$O\left(N^2\right)$，当输入是一张大图片时，计算量也会变得非常大，Transformer的具体计算量可以参考计算机视觉算法——Vision Transformer / Swin Transformer，Efficient Self Attention公式如下：$$\hat{K}=\mathrm{Reshape}\left(\frac{N}{R},C\cdot R\right)(K)$$$$K=\mathrm{Linear}(C\cdot R,C)(\hat{K})$$假定输入序列的维度为$N\times C$，第一个公式的意思时将输入序列$K$变成$\frac{N}{R}\times (C\cdot R)$大小，而$\mathrm{Linear}\left(C_{\text{in }},C_{\text{out }}\right)(\cdot )$意味着通过一个线性层将$C_{in}$-dimensional的输入变成$C_{\text{out }}$-dimensional，通过上面两个公式，将输入序列$K$的维度变为了$\frac{N}{R}\times C$，因此计算量从$O\left(N^2\right)$降为了$O\left(\frac{N^2}{R}\right)$。在Segformer中从第一层到第四层设置的$R$分别为$[64,16,4,1]$，我个人理解这一步相当于是增大了Patch，降低了分辨率，但是该操作不是在原始输入上进行的，而是在输入的Feature上，这样应该是可以减少分辨率降低带来的损失，到底损失了多少，在论文中我暂时还没有找到这一部分的Ablation Study对比结果。

3.1.3 Mix-FFN

解释Mix FFN就需要先提到Conditional Position Embeddingh，这个模块首次提出于2021年CVPR的论文《Conditional Positional Encodings for Vision Transformers》，解决的主要问题也就是Segformer中提到的，当测试和训练的图像分辨率不同时，绝对Position Embedding会面临插值而导致性能下降的问题，而Conditional Position Embedding就是通过卷积对不同Token进行位置关联。这里我们展开讲下：

在《Conditional Positional Encodings for Vision Transformers》论文中对不同Ecoding方式进行了对比，首先不加Positional Embedding肯定时不行的，Self-Attention的性质决定了对于同一个序列，任意排序，得到的结果将会时一样的，从实验结果看也是性能也是最差的，而Learnable和Sin-Cos会面临上面提到输入序列不可变长的问题，而Relative需要额外的计算且性能会下降。

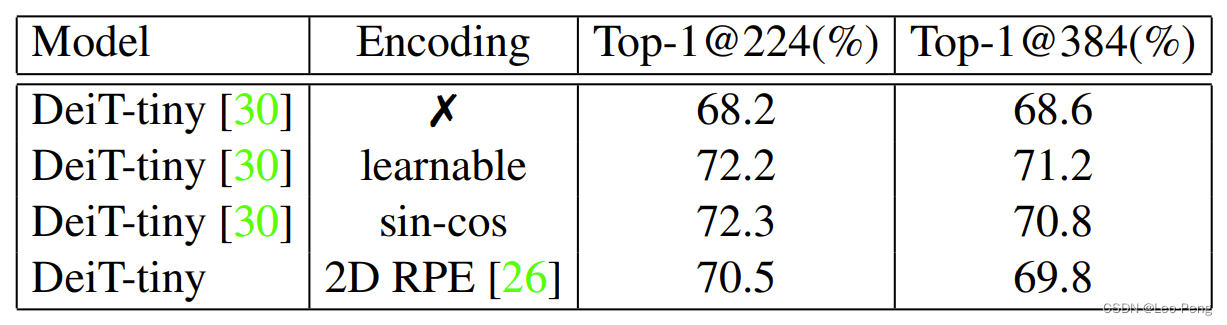
为此论文提出，一个好的Positional Encoding需要满足：

1. 使得网络具备空间不等价性（Permutation-Variant），但是具备平移等价性（Translation-Invariant）；
2. 能够处理不同长度的序列；
3. 可以提供一定程度的绝对位置信息。

但是平移不变性是好理解，当一个物体在图像中发生平移时，应该只时物体对应的Token发生了变化，但是Token Embeding的值应该是相同的，对于空间不等价性应该就是物体在图中发生平移后最后的Self Attention的结果应该是不同的。那么作者任务卷积正好就满足了上述这些特性，于是就设计了如下的Conditional Position Embedding模块：

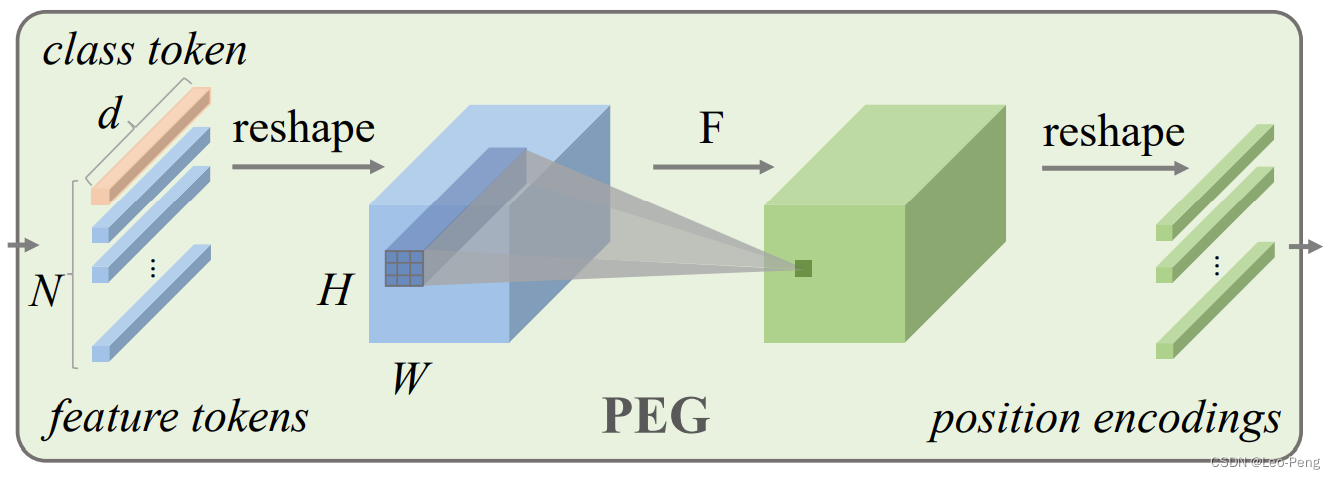
对应代码如下：

class PEG(nn.Module):
    def __init__(self, dim=256, k=3):
        self.proj = nn.Conv2d(dim, dim, k, 1, k//2, groups=dim)
        # Only for demo use, more complicated functions are effective too.
    def forward(self, x, H, W):
        B, N, C = x.shape
        cls_token, feat_token = x[:, 0], x[:, 1:] # cls token不参与PEG
        cnn_feat = feat_token.transpose(1, 2).view(B, C, H, W)
        x = self.proj(cnn_feat) + cnn_feat # 产生PE加上自身
        x = x.flatten(2).transpose(1, 2)
        x = torch.cat((cls_token.unsqueeze(1), x), dim=1)
    return x
1
2
3
4
5
6
7
8
9
10
11
12

其中self.porj部分是普通的2D卷积或者Depth-Wise卷积都可以，最关键的就是同通过卷积，我们在不同的Token间加上了一层隐式的关联，进而达到了空间不等价性。基于此作者提出了CPVT和CPVT-GAP的构架如下图所示：
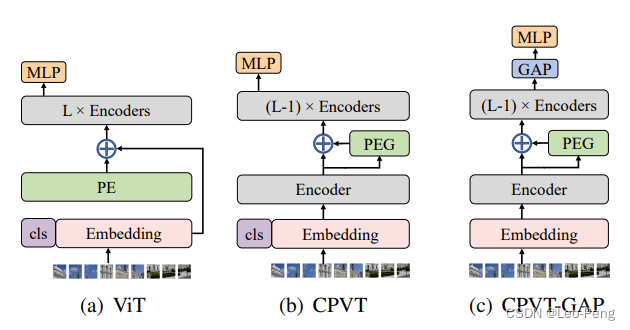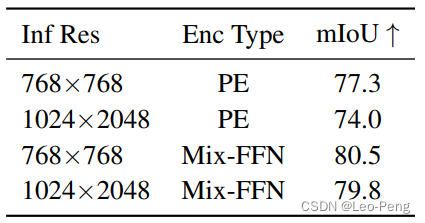
其中，GAP是为了将Cls Token从输入中拿掉，具体这里就不展开。

回到本篇文章，本论文认为语义分割中不需要Positional Encoding，因此作者设计了Mix-FNN，公式如下：$${\mathbf{x}}_{\text{out }}=\mathrm{MLP}\left(\mathrm{GELU}\left({\mathrm{Conv}}_{3\times 3}\left(\mathrm{MLP}\left({\mathbf{x}}_{in}\right)\right)\right)\right)+{\mathbf{x}}_{in},$$从上面网络大图中我们可以看到，该模块是替换原本的Feed Forward Layer，区别其实也就是在MLP的过程中假如了一个$3\times 3$的卷积，我觉得该卷积的作用和PEG的作用应该是类似的。作者在Ablation Study中有对比到，使用普通的Positional Encoding和Mix-FFN对于精度影响如下：

3.1.5 Lightweight All-MLP Decoder

Segmenter中的Decoder相对很多语义分割的模型的Decoder来说要简单很多，具体步骤如下：$${\hat{F}}_i=\mathrm{Linear}\left(C_i,C\right)\left(F_i\right),\forall i$$$${\hat{F}}_i=\text{ Upsample }\left(\frac{W}{4}\times \frac{W}{4}\right)\left({\hat{F}}_i\right),\forall i$$$$F=\mathrm{Linear}(4C,C)\left(\text{ Concat }\left({\hat{F}}_i\right)\right),\forall i$$$$M=\mathrm{Linear}\left(C,N_{cls}\right)(F),$$其中
第一步是将通过MLP调整Encoder输出特征$F_i$的通道数；
第二步是将分辨率分别为$\frac{1}{32}$，$\frac{1}{16}$，$\frac{1}{8}$的通道数上采样到$\frac{1}{4}$；
第三步将四种分辨率的上采样后的特征Concat到一起，然后再通过一个MLP将通道数调整到$C$；
第四步就是通过一个MLP将通道数调整到最后出的类别。
作者在论文中强调，如果简单的Decoder能取得比较好的效果得益于强大的Encoder，在论文中作者可视化了DeepLabv3+和Segformer的Encoder感受野：

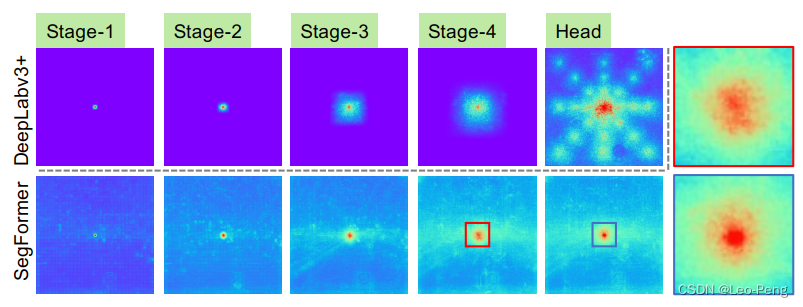
在Ablation Study中作者对比了使用ResNet50和本文的Backbone分别接MLP Decoder的精度区别：

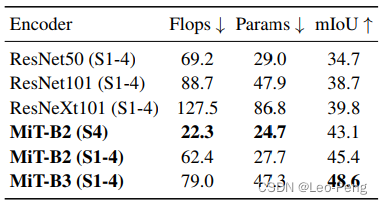
3.2 实验

本文做的对比实验还是非常丰富了，除了上文提到的一些针对模块的Ablation Study实验外，作者还与SOTA方法进行了对比，结果如下：

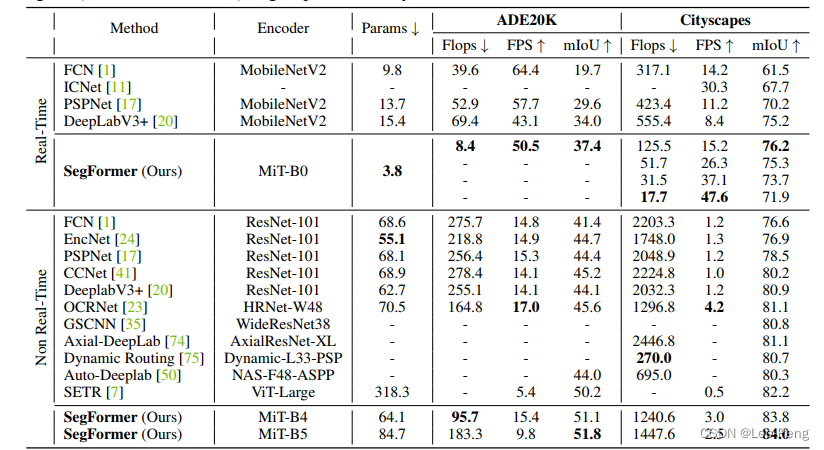
可以看到，无论是在实时还是非实时的方法上，Segformer都做到了很好的性能。作者还在Youtube上展示了DeepLabv3+和Segformer在不同噪声下的鲁棒性，效果也是非常惊艳，感兴趣的同学可以参考对比视频。

总而言之，Segformer相对SETR和Segmenter有了更大的进步，集众家之所长，性能也明显变好。