有限自动机字符串匹配

上一篇文章正则表达式，提到正则表达式是一种用来表示有限自动机所接受单词组合的语言，那么什么是有限自动机呢，以及它是如何进行字符串匹配的，下面来做详细介绍

什么是有限自动机

目前程序上利用不同的编程语言通过正则表达式进行字符串匹配，其底层是由有限自动机（Finite Automaton）来实现的，有限自动机简称 FA。FA 是一个有限状态的集合，还有一些从一个状态通向另一个状态的边，每条边上有一个符号，期中一个状态是初态，某些状态是终态，是一种状态转移图。形式上，FA 是一个五元组（S、Σ、δ(s, c)、S(0)、S(A)），其中各个分量表示如下：

S：是 FA 中的有限状态集合，包含错误状态 S(E)，通常 S(E) = S(0)。
Σ：是 FA 中的使用的字母表，通常 Σ 是转移图种边的标签集合。
δ(s, c)：是 FA 的状态转移函数。它将每个状态 s 和每个字符 c的组合（s, c）映射到下一个状态。在状态 S(i) 遇到输入字符 c，FA 将进行状态转移。
S(0)：是指定的起始状态，属于 S 的子集。
S(A)：是接受状态集合，属于 S 的子集。

下面是一个简单的 FA 示意图，表示的是一个以 a 开头，中间可以有 n 个连续的 c , 或者 n 个连续的 ba 组成的字符串，比如 a、aba、abababa、accccba、acccbababa、ababacccbacc 等，正则表达式可以表示为 a((ba)c)*

字符串匹配过程

有限自动机开始于状态 S(0) ，每次读入字符串中的一个字符 c，状态就会通过 δ(s, c) 进行一次状态转移，每当当前达到的状态 s 属于 S(A) 时，就说自动机 FA 接受了迄今为止所读入的字符串，同时达到 S(A) 时主串（Text）的下标就是匹配完成的结束位置。如果没有被接受的输入则匹配失败。有限自动机字符串匹配主要分为两步：构造字符串匹配自动机、进行主串匹配。

1. 字符串匹配自动机

字符串匹配自动机是针对模式串 P 来构建的，类似于 KMP 算法构造 Next 数组。

假设模式串 P 的长度为 m，则有限自动机对应的分量分别设定为：

状态集合 S = {0, 1, 2, …, m-1, m}
字母表 Σ 为 P 包含的所有字符集合
起始状态 S(0) = 0
接受状态 S(A) = {m}
状态转移函数 δ(s, c) 下面会详细介绍

为了定义状态转移函数 δ(s, c) ，我们先引入一个后缀函数 φ(t)，φ(t) 是一个从输入文本（Σ* ）到状态集合（S）的映射，φ(t) 表示 t 的后缀同时是 P 前缀的情况下，t 后缀的最长长度。并且认为空字符串 ϵ 是任意字符串的后缀，所以后缀函数是良定义（well-defined）的。
例如：设定模式串 P = ab，则

φ(ϵ) = 0,
φ(a) = 1，t = a 的后缀在模式串 P = ab 的最长前缀是 a，长度为 1
φ(ca) = 1，t = ca 的后缀在模式串 P = ab 的最长前缀是 a，长度为 1
φ(cc) = 0，t = ca 的后缀在模式串 P = ab 的最长前缀是 ϵ，长度为 0
φ(cab) = 2，t = cab 的后缀在模式串 P = ab 的最长前缀是 ab，长度为 2
φ(cabc) = 0，t = cabc 的后缀在模式串 P = ab 的最长前缀是 ϵ，长度为 0

在引入后缀函数 φ(t) 的基础下，对于任意的状态 s 和字符 c，状态转移函数 δ(s, c) 的定义为

δ(s, c) = φ(P(s)c)

• P(s) 表示模式串 P 在状态 s 时的前缀
• P(s)c 表示在 P(s) 后拼接字符 c。

2. 字符串匹配

下面我们通过一个例子来说明对应的状态转移图是什么样子，状态是怎么转移的，以及如何与主串进行匹配：

例：
模式串 P = ababcab

构建状态转移图如下：

• 它可以接受所有以 P 结尾的字符串，初始状态 S(0) = 0，接受状态 S(A) = {7}；
• 向右的边表示匹配模式串 P 与主串输入字符匹配成功；
• 向左的边表示匹配失败后对于模式串的回溯；
• 直接匹配失败回溯到初始状态 S(0) 的边并没有画出来
  

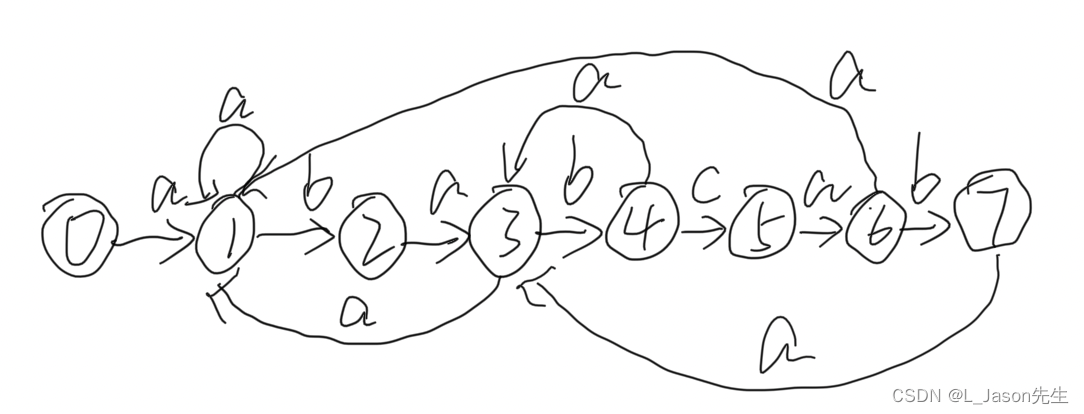
下表表示转移函数 δ(s, c) 和模式串 P 的对应关系
在「状态」s 的基础上输入 a、b、c 会到达对应表格种的状态，以及匹配成功后对应模式串中的字符：

匹配过程

设定
主串 T = abababcabac
主串 T 字符下标从 1 开始，经过 φ(P(s)c) 在主串的位置 9 找到一个模式串 P 的完全匹配
结果：成功匹配，匹配位置以 9 结尾

代码实现以及复杂度分析

1. 状态转移函数

2. 匹配函数