【序列比对】Needleman-Wunsch（全局）和Smith-Waterman（局部）算法py实现（多条回溯路径，三叉树思路，超详细注释）

Needleman-Wunsch和Smith-Waterman算法py实现（多条回溯路径）

话不多说，直接上结果图，多条回溯路径。

原理

代码详解（以NW为例）

导入包以及参数设置

import numpy as np

sequence_1 = "AACGTACTCAAGTCT"
sequence_2 = "TCGTACTCTAACGAT"
match = 9
mismatch = -6
gap = -2
1
2
3
4
5
6
7

创建得分矩阵

• 创建得分矩阵，行数为第一条序列长度加一，列数为第二条序列长度加二
• 创建是否匹配的矩阵，这个矩阵的长宽就分别是两条序列的长度了。如果匹配了，对应的格子就是匹配的得分，反之就是不匹配的得分
• 动态规划的思想算每个格子的得分，每个格子需要考虑其左、上、左上的值，也可以说是考虑序列一、序列二引入空缺或直接匹配的最大值

# 创建得分矩阵，行数为第一条序列长度加一，列数为第二条序列长度加二
Score = np.zeros((len(sequence_1) + 1, len(sequence_2) + 1))
# 创建是否匹配的矩阵，这个矩阵的长宽就分别是两条序列的长度了。如果匹配了，对应的格子就是匹配的得分，反之就是不匹配的得分
Match_or_not = np.zeros((len(sequence_1), len(sequence_2)))
for i in range(len(sequence_1)):
    for j in range(len(sequence_2)):
        if sequence_1[i] == sequence_2[j]:
            Match_or_not[i][j] = match
        else:
            Match_or_not[i][j] = mismatch

# 填得分矩阵
# 第一步：初始化第一行和第一列
for i in range(len(sequence_1) + 1):
    Score[i][0] = i * gap
for j in range(len(sequence_2) + 1):
    Score[0][j] = j * gap
# 第二步：动态规划的思想算每个格子的得分，每个格子需要考虑其左、上、左上的值，也可以说是考虑序列一、序列二引入空缺或直接匹配的最大值
for i in range(1, len(sequence_1) + 1):
    for j in range(1, len(sequence_2) + 1):
        Score[i][j] = max(Score[i - 1][j - 1] + Match_or_not[i - 1][j - 1],
                          Score[i - 1][j] + gap,
                          Score[i][j - 1] + gap)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

看看得分矩阵长啥样吧

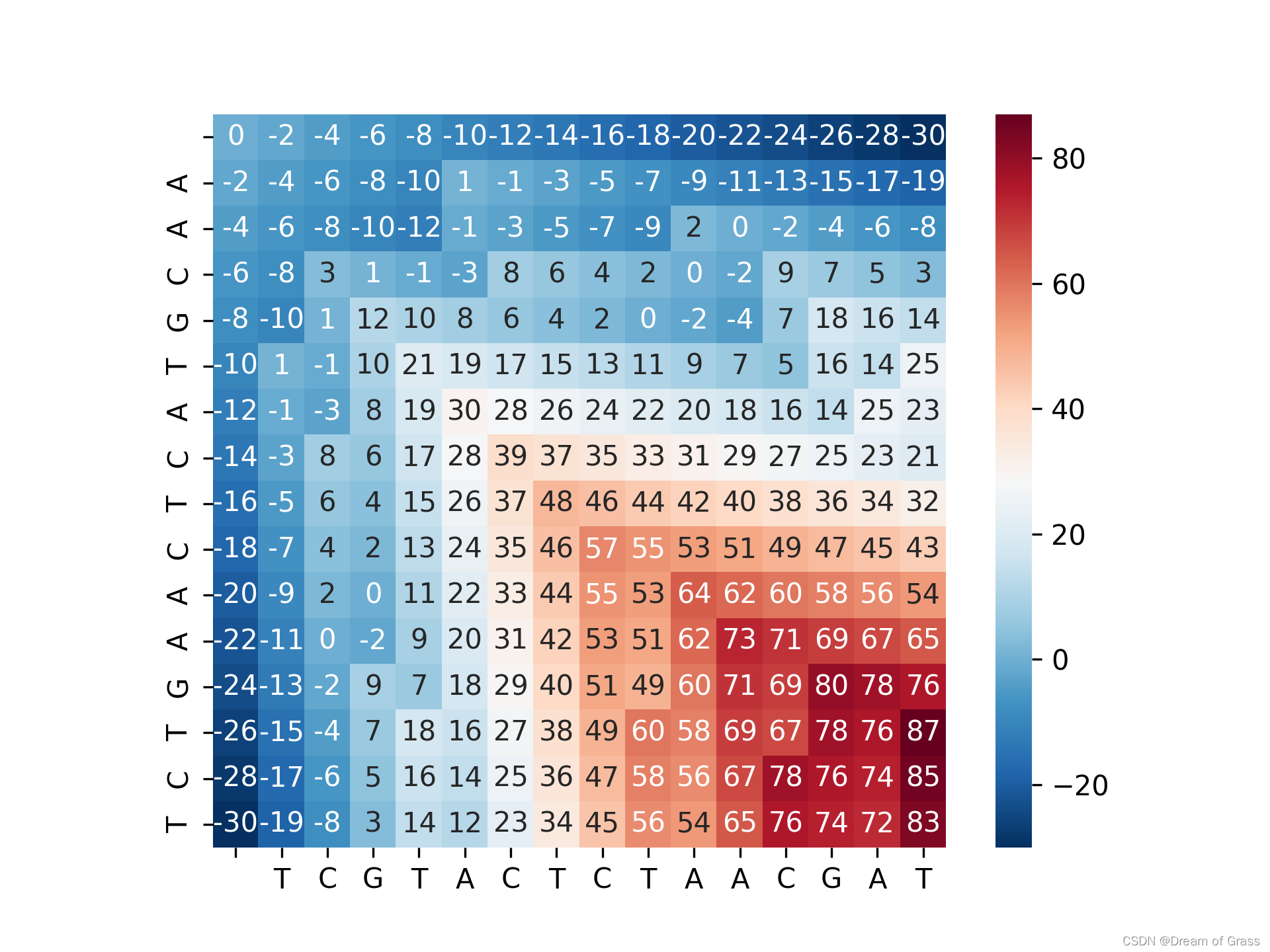
回溯

我们需要考虑的是可能会有多条回溯路径。全局比对的回溯是从右下角开始，左上角结束，其中可能会有分叉点。我们可以把右下角看成是一个树的根，矩阵中的每个值看成是一个节点。每个节点都可能会有三个子节点：左，上，对角线。分别对应了回溯的方向。而整个回溯的过程也就是遍历这颗三叉树的过程，严谨的说是从根节点遍历每个叶子节点的过程。

# 开始回溯
'''
我们需要考虑的是可能会有多条回溯路径。
全局比对的回溯是从右下角开始，左上角结束，其中可能会有分叉点。
我们可以把右下角看成是一个树的根，矩阵中的每个值看成是一个节点。
每个节点都可能会有三个子节点：左，上，对角线。分别对应了回溯的方向。
而整个回溯的过程也就是遍历这颗三叉树的过程，严谨的说是从根节点遍历每个叶子节点的过程。
'''


class Node:
    # 用类来建立三叉树节点，属性包括了行、列、得分、左子树、上子树、对角线子树
    def __init__(self, row=None, col=None, score=None):
        self.row = row
        self.col = col
        self.score = score
        self.left = None
        self.up = None
        self.diag = None


def isLeaf(self):
    # 判断是否是叶子节点
    return self.left is None and self.up is None and self.diag is None
    # 递归的函数查找从根节点到每个叶节点的路径


# 回溯路径的个数、回溯路径中的行号和列号
traceback_pathway_number = 0
traceback_pathway_row = [[]]
traceback_pathway_col = [[]]


def SaveRootToLeafPaths(Node, path_row, path_col):
    # 如果没有子树了
    if Node is None:
        return
    # 包含当前节点的路径
    path_row.append(Node.row)
    path_col.append(Node.col)
    global traceback_pathway_number
    global traceback_pathway_row
    global traceback_pathway_col
    # 如果找到叶节点，保存路径
    if isLeaf(Node):
        if traceback_pathway_number == 0:
            traceback_pathway_row[traceback_pathway_number] = list(path_row)
            traceback_pathway_col[traceback_pathway_number] = list(path_col)
        else:
            traceback_pathway_row += [list(path_row)]
            traceback_pathway_col += [list(path_col)]
        traceback_pathway_number += 1
    # 递归左、上、对角子树
    SaveRootToLeafPaths(Node.left, path_row, path_col)
    SaveRootToLeafPaths(Node.up, path_row, path_col)
    SaveRootToLeafPaths(Node.diag, path_row, path_col)
    # 回溯，出栈
    path_row.pop()
    path_col.pop()


# 建立三叉树，为 Score 矩阵里所有值都找到它的左、上、对角子树，用一个二位列表来存储节点
NodeTree = [[Node() for _ in range(len(sequence_2) + 1)] for _ in range(len(sequence_1) + 1)]
# 先把节点们的行号列号和得分记录下来
for i in range(len(sequence_1) + 1):
    for j in range(len(sequence_2) + 1):
        NodeTree[i][j].row = i
        NodeTree[i][j].col = j
        NodeTree[i][j].score = Score[i][j]
# 设置第一列和第一行的节点的上子树和左子树（其实也能在下面这个大循环里设置，但是这样可读性更高）
for i in range(1, len(sequence_1) + 1):
    NodeTree[i][0].up = NodeTree[i - 1][0]
for j in range(1, len(sequence_2) + 1):
    NodeTree[0][j].left = NodeTree[0][j - 1]
# 设置剩下的节点
for i in range(1, len(sequence_1) + 1):
    for j in range(1, len(sequence_2) + 1):
        if (Score[i][j] == Score[i - 1][j - 1] + Match_or_not[i - 1][j - 1]):
            NodeTree[i][j].diag = NodeTree[i - 1][j - 1]
        if (Score[i][j] == Score[i - 1][j] + gap):
            NodeTree[i][j].up = NodeTree[i - 1][j]
        if (Score[i][j] == Score[i][j - 1] + gap):
            NodeTree[i][j].left = NodeTree[i][j - 1]
# 遍历树并保存路径
SaveRootToLeafPaths(NodeTree[len(sequence_1)][len(sequence_2)], [], [])
# 改成numpy的ndarray类型，更加方便！
traceback_pathway_row = np.array(traceback_pathway_row)
traceback_pathway_col = np.array(traceback_pathway_col)
# 记录一下回溯时走不走左边或上边，如果走就记为1，不走就记为0
Go_left = traceback_pathway_col[:, range(traceback_pathway_col.shape[1] - 1)] - traceback_pathway_col[:, range(1,
                                                                                                               traceback_pathway_col.shape[
                                                                                                                   1])]
Go_up = traceback_pathway_row[:, range(traceback_pathway_row.shape[1] - 1)] - traceback_pathway_row[:,
                                                                              range(1, traceback_pathway_row.shape[1])]
# 用列表来存储序列一和序列二比对后的结果
seq1_align_set = []
seq2_align_set = []
print("总共有{}个比对结果".format(traceback_pathway_number))
for tpn in range(traceback_pathway_number):
    '''
    下面其实就是经典的nw回溯的代码了，这部分的原理可以参考nw算法回溯的伪代码。
    唯一不同的就是我们是多条回溯路径，所以有多少条路经就得循环多少次。
    值得一提的是，回溯过去的序列是逆序的，
    在python中字符串逆置十分方便，只需要合理利用切片，如：str[::-1]即可。
    '''
    seq1_align = ''
    seq2_align = ''
    i = len(sequence_1)
    j = len(sequence_2)
    k = 0
    while i > 0 or j > 0:
        if i > 0 and j > 0 and Go_left[tpn][k] and Go_up[tpn][k]:
            seq1_align += sequence_1[i - 1]
            seq2_align += sequence_2[j - 1]
            i -= 1
            j -= 1
        elif i > 0 and not (Go_left[tpn][k]) and Go_up[tpn][k]:
            seq1_align += sequence_1[i - 1]
            seq2_align += '-'
            i -= 1
        elif j > 0 and Go_left[tpn][k] and not (Go_up[tpn][k]):
            seq1_align += '-'
            seq2_align += sequence_2[j - 1]
            j -= 1
        k += 1
    seq1_align_set += [seq1_align[::-1]]
    seq2_align_set += [seq2_align[::-1]]
    print("下面是第{}个".format(tpn + 1))
    print(seq1_align[::-1])
    print(seq2_align[::-1])
    print(' ')
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131

输出

总共有15个比对结果
下面是第1个
AA-CGTACTC-AA-G-TCT
–TCGTACTCTAACGAT–

下面是第2个
A-ACGTACTC-AA-G-TCT
-T-CGTACTCTAACGAT–

下面是第3个
-AACGTACTC-AA-G-TCT
T–CGTACTCTAACGAT–

下面是第4个
AA-CGTACTC-AAGTC–T
–TCGTACTCTAA–CGAT

下面是第5个
A-ACGTACTC-AAGTC–T
-T-CGTACTCTAA–CGAT

下面是第6个
-AACGTACTC-AAGTC–T
T–CGTACTCTAA–CGAT

下面是第7个
AA-CGTACTC-AA-GTC-T
–TCGTACTCTAACG–AT

下面是第8个
A-ACGTACTC-AA-GTC-T
-T-CGTACTCTAACG–AT

下面是第9个
-AACGTACTC-AA-GTC-T
T–CGTACTCTAACG–AT

下面是第10个
AA-CGTACTC-AA-GT-CT
–TCGTACTCTAACG-A-T

下面是第11个
A-ACGTACTC-AA-GT-CT
-T-CGTACTCTAACG-A-T

下面是第12个
-AACGTACTC-AA-GT-CT
T–CGTACTCTAACG-A-T

下面是第13个
AA-CGTACTC-AA-G-TCT
–TCGTACTCTAACGA–T

下面是第14个
A-ACGTACTC-AA-G-TCT
-T-CGTACTCTAACGA–T

下面是第15个
-AACGTACTC-AA-G-TCT
T–CGTACTCTAACGA–T

画一下回溯的路径

可视化代码

'''
下面就是得分矩阵的热图以及回溯路径（格子）画出来了
'''
import pandas as pd
import seaborn as sns
from matplotlib import pyplot as plt

Score = pd.DataFrame(Score)
row_name = list(sequence_1)
row_name.insert(0, ' ')
col_name = list(sequence_2)
col_name.insert(0, ' ')
Score.index = row_name
Score.columns = col_name
traceback_way_mat = np.ones([len(sequence_1) + 1, len(sequence_2) + 1])

for i in range(traceback_pathway_row.shape[0]):
    traceback_way_mat[traceback_pathway_row[i][:], traceback_pathway_col[i][:]] = 0
ax1 = sns.heatmap(Score, linecolor='white', linewidth=0, square=True, cmap="RdBu_r", annot=True)
plt.savefig('nw_Heatmap with annotation.png',dpi=300)
plt.show()
ax2 = sns.heatmap(Score, linecolor='white', linewidth=0, square=True, cmap="RdBu_r")
plt.savefig('nw_Heatmap.png',dpi=300)
plt.show()
ax3 = sns.heatmap(Score, linecolor='white', linewidth=0, square=True, cmap="RdBu_r", mask=traceback_way_mat)
plt.savefig('nw_Heatmap_traceback',dpi=300)
plt.show()

#%%
# params={'font.family':'serif',
#         'font.serif':'Times New Roman',
#         'font.style':'normal',#'italic'
#         'font.weight':'normal', #or 'blod'
#         'font.size':12,#or large,small
#         'figure.figsize':(6,6)
#         }
plt.rcParams['figure.figsize'] = (6, 6)
# plt.rcParams.update(params)
for j in range(traceback_pathway_col.shape[0]):
    fig = plt.figure()

    ax = plt.axes()
    plt.grid(zorder=0, linestyle='-.')
    for i in range(traceback_pathway_col.shape[1]-1):
        xs = traceback_pathway_col[j][i]
        ys = traceback_pathway_row[j][i]
        xe = traceback_pathway_col[j][i+1]
        ye = traceback_pathway_row[j][i+1]
        ax.arrow(xs, ys, xe-xs, ye-ys, length_includes_head=True,head_width=0.3, fc='crimson', ec='hotpink',zorder=10)

    ax.set_xlim(-0.5, len(col_name)-0.5)
    ax.set_ylim(-0.5, len(col_name)-0.5)
    plt.xticks(np.arange(0,len(col_name),1), col_name)
    plt.yticks(np.arange(0,len(row_name),1), row_name)
    ax.xaxis.set_ticks_position('top')
    ax.invert_yaxis()
    ax.set_title('No.{}'.format(j+1),fontsize=12,color='k',loc='left',y=0.86,x=0.3,fontweight='bold')
    ax.set_title('{}{}{}'.format(seq1_align_set[j],'\n',seq2_align_set[j]),fontsize=16,fontfamily ='monospace',color='k',fontweight='bold',y=0.83,x=0.7)
    # plt.rcParams['figure.figsize'] = (6, 6)
    plt.savefig('nw_No.{}'.format(j+1)+'.png',dpi=300)
    plt.show()

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62

Smith Waterman算法

局部比对的和全局比对差不多，只需再几个小细节上改改就行，大家可以在两个代码之间找找茬~

完整代码

NW

import numpy as np

sequence_1 = "AACGTACTCAAGTCT"
sequence_2 = "TCGTACTCTAACGAT"
match = 9
mismatch = -6
gap = -2

# 创建得分矩阵，行数为第一条序列长度加一，列数为第二条序列长度加二
Score = np.zeros((len(sequence_1) + 1, len(sequence_2) + 1))
# 创建是否匹配的矩阵，这个矩阵的长宽就分别是两条序列的长度了。如果匹配了，对应的格子就是匹配的得分，反之就是不匹配的得分
Match_or_not = np.zeros((len(sequence_1), len(sequence_2)))
for i in range(len(sequence_1)):
    for j in range(len(sequence_2)):
        if sequence_1[i] == sequence_2[j]:
            Match_or_not[i][j] = match
        else:
            Match_or_not[i][j] = mismatch

# 填得分矩阵
# 第一步：初始化第一行和第一列
for i in range(len(sequence_1) + 1):
    Score[i][0] = i * gap
for j in range(len(sequence_2) + 1):
    Score[0][j] = j * gap
# 第二步：动态规划的思想算每个格子的得分，每个格子需要考虑其左、上、左上的值，也可以说是考虑序列一、序列二引入空缺或直接匹配的最大值
for i in range(1, len(sequence_1) + 1):
    for j in range(1, len(sequence_2) + 1):
        Score[i][j] = max(Score[i - 1][j - 1] + Match_or_not[i - 1][j - 1],
                          Score[i - 1][j] + gap,
                          Score[i][j - 1] + gap)

# 开始回溯
'''
我们需要考虑的是可能会有多条回溯路径。
全局比对的回溯是从右下角开始，左上角结束，其中可能会有分叉点。
我们可以把右下角看成是一个树的根，矩阵中的每个值看成是一个节点。
每个节点都可能会有三个子节点：左，上，对角线。分别对应了回溯的方向。
而整个回溯的过程也就是遍历这颗三叉树的过程，严谨的说是从根节点遍历每个叶子节点的过程。
'''


class Node:
    # 用类来建立三叉树节点，属性包括了行、列、得分、左子树、上子树、对角线子树
    def __init__(self, row=None, col=None, score=None):
        self.row = row
        self.col = col
        self.score = score
        self.left = None
        self.up = None
        self.diag = None


def isLeaf(self):
    # 判断是否是叶子节点
    return self.left is None and self.up is None and self.diag is None
    # 递归的函数查找从根节点到每个叶节点的路径


# 回溯路径的个数、回溯路径中的行号和列号
traceback_pathway_number = 0
traceback_pathway_row = [[]]
traceback_pathway_col = [[]]


def SaveRootToLeafPaths(Node, path_row, path_col):
    # 如果没有子树了
    if Node is None:
        return
    # 包含当前节点的路径
    path_row.append(Node.row)
    path_col.append(Node.col)
    global traceback_pathway_number
    global traceback_pathway_row
    global traceback_pathway_col
    # 如果找到叶节点，保存路径
    if isLeaf(Node):
        if traceback_pathway_number == 0:
            traceback_pathway_row[traceback_pathway_number] = list(path_row)
            traceback_pathway_col[traceback_pathway_number] = list(path_col)
        else:
            traceback_pathway_row += [list(path_row)]
            traceback_pathway_col += [list(path_col)]
        traceback_pathway_number += 1
    # 递归左、上、对角子树
    SaveRootToLeafPaths(Node.left, path_row, path_col)
    SaveRootToLeafPaths(Node.up, path_row, path_col)
    SaveRootToLeafPaths(Node.diag, path_row, path_col)
    # 回溯，出栈
    path_row.pop()
    path_col.pop()


# 建立三叉树，为 Score 矩阵里所有值都找到它的左、上、对角子树，用一个二位列表来存储节点
NodeTree = [[Node() for _ in range(len(sequence_2) + 1)] for _ in range(len(sequence_1) + 1)]
# 先把节点们的行号列号和得分记录下来
for i in range(len(sequence_1) + 1):
    for j in range(len(sequence_2) + 1):
        NodeTree[i][j].row = i
        NodeTree[i][j].col = j
        NodeTree[i][j].score = Score[i][j]
# 设置第一列和第一行的节点的上子树和左子树（其实也能在下面这个大循环里设置，但是这样可读性更高）
for i in range(1, len(sequence_1) + 1):
    NodeTree[i][0].up = NodeTree[i - 1][0]
for j in range(1, len(sequence_2) + 1):
    NodeTree[0][j].left = NodeTree[0][j - 1]
# 设置剩下的节点
for i in range(1, len(sequence_1) + 1):
    for j in range(1, len(sequence_2) + 1):
        if (Score[i][j] == Score[i - 1][j - 1] + Match_or_not[i - 1][j - 1]):
            NodeTree[i][j].diag = NodeTree[i - 1][j - 1]
        if (Score[i][j] == Score[i - 1][j] + gap):
            NodeTree[i][j].up = NodeTree[i - 1][j]
        if (Score[i][j] == Score[i][j - 1] + gap):
            NodeTree[i][j].left = NodeTree[i][j - 1]
# 遍历树并保存路径
SaveRootToLeafPaths(NodeTree[len(sequence_1)][len(sequence_2)], [], [])
# 改成numpy的ndarray类型，更加方便！
traceback_pathway_row = np.array(traceback_pathway_row)
traceback_pathway_col = np.array(traceback_pathway_col)
# 记录一下回溯时走不走左边或上边，如果走就记为1，不走就记为0
Go_left = traceback_pathway_col[:, range(traceback_pathway_col.shape[1] - 1)] - traceback_pathway_col[:, range(1,
                                                                                                               traceback_pathway_col.shape[
                                                                                                                   1])]
Go_up = traceback_pathway_row[:, range(traceback_pathway_row.shape[1] - 1)] - traceback_pathway_row[:,
                                                                              range(1, traceback_pathway_row.shape[1])]
# 用列表来存储序列一和序列二比对后的结果
seq1_align_set = []
seq2_align_set = []
print("总共有{}个比对结果".format(traceback_pathway_number))
for tpn in range(traceback_pathway_number):
    '''
    下面其实就是经典的nw回溯的代码了，这部分的原理可以参考nw算法回溯的伪代码。
    唯一不同的就是我们是多条回溯路径，所以有多少条路经就得循环多少次。
    值得一提的是，回溯过去的序列是逆序的，
    在python中字符串逆置十分方便，只需要合理利用切片，如：str[::-1]即可。
    '''
    seq1_align = ''
    seq2_align = ''
    i = len(sequence_1)
    j = len(sequence_2)
    k = 0
    while i > 0 or j > 0:
        if i > 0 and j > 0 and Go_left[tpn][k] and Go_up[tpn][k]:
            seq1_align += sequence_1[i - 1]
            seq2_align += sequence_2[j - 1]
            i -= 1
            j -= 1
        elif i > 0 and not (Go_left[tpn][k]) and Go_up[tpn][k]:
            seq1_align += sequence_1[i - 1]
            seq2_align += '-'
            i -= 1
        elif j > 0 and Go_left[tpn][k] and not (Go_up[tpn][k]):
            seq1_align += '-'
            seq2_align += sequence_2[j - 1]
            j -= 1
        k += 1
    seq1_align_set += [seq1_align[::-1]]
    seq2_align_set += [seq2_align[::-1]]
    print("下面是第{}个".format(tpn + 1))
    print(seq1_align[::-1])
    print(seq2_align[::-1])
    print(' ')
#%%
'''
下面就是得分矩阵的热图以及回溯路径（格子）画出来了
'''
import pandas as pd
import seaborn as sns
from matplotlib import pyplot as plt

Score = pd.DataFrame(Score)
row_name = list(sequence_1)
row_name.insert(0, ' ')
col_name = list(sequence_2)
col_name.insert(0, ' ')
Score.index = row_name
Score.columns = col_name
traceback_way_mat = np.ones([len(sequence_1) + 1, len(sequence_2) + 1])

for i in range(traceback_pathway_row.shape[0]):
    traceback_way_mat[traceback_pathway_row[i][:], traceback_pathway_col[i][:]] = 0
ax1 = sns.heatmap(Score, linecolor='white', linewidth=0, square=True, cmap="RdBu_r", annot=True)
plt.savefig('nw_Heatmap with annotation.png',dpi=300)
plt.show()
ax2 = sns.heatmap(Score, linecolor='white', linewidth=0, square=True, cmap="RdBu_r")
plt.savefig('nw_Heatmap.png',dpi=300)
plt.show()
ax3 = sns.heatmap(Score, linecolor='white', linewidth=0, square=True, cmap="RdBu_r", mask=traceback_way_mat)
plt.savefig('nw_Heatmap_traceback',dpi=300)
plt.show()

#%%
# params={'font.family':'serif',
#         'font.serif':'Times New Roman',
#         'font.style':'normal',#'italic'
#         'font.weight':'normal', #or 'blod'
#         'font.size':12,#or large,small
#         'figure.figsize':(6,6)
#         }
plt.rcParams['figure.figsize'] = (6, 6)
# plt.rcParams.update(params)
for j in range(traceback_pathway_col.shape[0]):
    fig = plt.figure()

    ax = plt.axes()
    plt.grid(zorder=0, linestyle='-.')
    for i in range(traceback_pathway_col.shape[1]-1):
        xs = traceback_pathway_col[j][i]
        ys = traceback_pathway_row[j][i]
        xe = traceback_pathway_col[j][i+1]
        ye = traceback_pathway_row[j][i+1]
        ax.arrow(xs, ys, xe-xs, ye-ys, length_includes_head=True,head_width=0.3, fc='crimson', ec='hotpink',zorder=10)

    ax.set_xlim(-0.5, len(col_name)-0.5)
    ax.set_ylim(-0.5, len(col_name)-0.5)
    plt.xticks(np.arange(0,len(col_name),1), col_name)
    plt.yticks(np.arange(0,len(row_name),1), row_name)
    ax.xaxis.set_ticks_position('top')
    ax.invert_yaxis()
    ax.set_title('No.{}'.format(j+1),fontsize=12,color='k',loc='left',y=0.86,x=0.3,fontweight='bold')
    ax.set_title('{}{}{}'.format(seq1_align_set[j],'\n',seq2_align_set[j]),fontsize=16,fontfamily ='monospace',color='k',fontweight='bold',y=0.83,x=0.7)
    # plt.rcParams['figure.figsize'] = (6, 6)
    plt.savefig('nw_No.{}'.format(j+1)+'.png',dpi=300)
    plt.show()

import datetime
print("这是代码执行时间: ",datetime.datetime.now())


1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230

SW

import numpy as np

sequence_1 = "AACGTACTCAAGTCT"
sequence_2 = "TCGTACTCTAACGAT"
match = 9
mismatch = -6
gap = -2

# 创建得分矩阵，行数为第一条序列长度加一，列数为第二条序列长度加二
Score = np.zeros((len(sequence_1) + 1, len(sequence_2) + 1))
# 创建是否匹配的矩阵，这个矩阵的长宽就分别是两条序列的长度了。如果匹配了，对应的格子就是匹配的得分，反之就是不匹配的得分
Match_or_not = np.zeros((len(sequence_1), len(sequence_2)))
for i in range(len(sequence_1)):
    for j in range(len(sequence_2)):
        if sequence_1[i] == sequence_2[j]:
            Match_or_not[i][j] = match
        else:
            Match_or_not[i][j] = mismatch

# 填得分矩阵
# 第一步：初始化第一行和第一列
for i in range(len(sequence_1) + 1):
    Score[i][0] = 0
for j in range(len(sequence_2) + 1):
    Score[0][j] = 0
# 第二步：动态规划的思想算每个格子的得分，每个格子需要考虑其左、上、左上的值，也可以说是考虑序列一、序列二引入空缺或直接匹配的最大值
for i in range(1, len(sequence_1) + 1):
    for j in range(1, len(sequence_2) + 1):
        Score[i][j] = max(Score[i - 1][j - 1] + Match_or_not[i - 1][j - 1],
                          Score[i - 1][j] + gap,
                          Score[i][j - 1] + gap, 0)

# 开始回溯
'''
我们需要考虑的是可能会有多条回溯路径。
全局比对的回溯是从右下角开始，左上角结束，其中可能会有分叉点。
我们可以把右下角看成是一个树的根，矩阵中的每个值看成是一个节点。
每个节点都可能会有三个子节点：左，上，对角线。分别对应了回溯的方向。
而整个回溯的过程也就是遍历这颗三叉树的过程，严谨的说是从根节点遍历每个叶子节点的过程。
'''


class Node:
    # 用类来建立三叉树节点，属性包括了行、列、得分、左子树、上子树、对角线子树
    def __init__(self, row=None, col=None, score=None):
        self.row = row
        self.col = col
        self.score = score
        self.left = None
        self.up = None
        self.diag = None


def isLeaf(self):
    # 判断是否是叶子节点
    return self.left is None and self.up is None and self.diag is None
    # 递归的函数查找从根节点到每个叶节点的路径


# 回溯路径的个数、回溯路径中的行号和列号
traceback_pathway_number = 0
traceback_pathway_row = [[]]
traceback_pathway_col = [[]]


def SaveRootToLeafPaths(Node, path_row, path_col):
    # 如果没有子树了
    if Node is None:
        return
    # 包含当前节点的路径
    path_row.append(Node.row)
    path_col.append(Node.col)
    global traceback_pathway_number
    global traceback_pathway_row
    global traceback_pathway_col
    # 如果找到叶节点，保存路径
    if isLeaf(Node):
        if traceback_pathway_number == 0:
            traceback_pathway_row[traceback_pathway_number] = list(path_row)
            traceback_pathway_col[traceback_pathway_number] = list(path_col)
        else:
            traceback_pathway_row += [list(path_row)]
            traceback_pathway_col += [list(path_col)]
        traceback_pathway_number += 1
    # 递归左、上、对角子树
    SaveRootToLeafPaths(Node.left, path_row, path_col)
    SaveRootToLeafPaths(Node.up, path_row, path_col)
    SaveRootToLeafPaths(Node.diag, path_row, path_col)
    # 回溯，出栈
    path_row.pop()
    path_col.pop()


# 建立三叉树，为 Score 矩阵里所有值都找到它的左、上、对角子树，用一个二位列表来存储节点
NodeTree = [[Node() for _ in range(len(sequence_2) + 1)] for _ in range(len(sequence_1) + 1)]
# 先把节点们的行号列号和得分记录下来
for i in range(len(sequence_1) + 1):
    for j in range(len(sequence_2) + 1):
        NodeTree[i][j].row = i
        NodeTree[i][j].col = j
        NodeTree[i][j].score = Score[i][j]
# 设置第一列和第一行的节点的上子树和左子树（其实也能在下面这个大循环里设置，但是这样可读性更高）
for i in range(1, len(sequence_1) + 1):
    NodeTree[i][0].up = NodeTree[i - 1][0]
for j in range(1, len(sequence_2) + 1):
    NodeTree[0][j].left = NodeTree[0][j - 1]
# 设置剩下的节点
for i in range(1, len(sequence_1) + 1):
    for j in range(1, len(sequence_2) + 1):
        if (Score[i][j] == Score[i - 1][j - 1] + Match_or_not[i - 1][j - 1]):
            NodeTree[i][j].diag = NodeTree[i - 1][j - 1]
        if (Score[i][j] == Score[i - 1][j] + gap):
            NodeTree[i][j].up = NodeTree[i - 1][j]
        if (Score[i][j] == Score[i][j - 1] + gap):
            NodeTree[i][j].left = NodeTree[i][j - 1]
# 遍历树并保存路径
r, c = np.where(Score == np.max(Score))
SaveRootToLeafPaths(NodeTree[int(r)][int(c)], [], [])
# 改成numpy的ndarray类型，更加方便！
traceback_pathway_row = np.array(traceback_pathway_row)
traceback_pathway_col = np.array(traceback_pathway_col)
# 记录一下回溯时走不走左边或上边，如果走就记为1，不走就记为0
Go_left = traceback_pathway_col[:, range(traceback_pathway_col.shape[1] - 1)] - traceback_pathway_col[:, range(1,
                                                                                                               traceback_pathway_col.shape[
                                                                                                                   1])]
Go_up = traceback_pathway_row[:, range(traceback_pathway_row.shape[1] - 1)] - traceback_pathway_row[:,
                                                                              range(1, traceback_pathway_row.shape[1])]
# 用列表来存储序列一和序列二比对后的结果
seq1_align_set = []
seq2_align_set = []
print("总共有{}个比对结果".format(traceback_pathway_number))
for tpn in range(traceback_pathway_number):
    '''
    下面其实就是经典的nw回溯的代码了，这部分的原理可以参考nw算法回溯的伪代码。
    唯一不同的就是我们是多条回溯路径，所以有多少条路经就得循环多少次。
    值得一提的是，回溯过去的序列是逆序的，
    在python中字符串逆置十分方便，只需要合理利用切片，如：str[::-1]即可。
    '''
    seq1_align = ''
    seq2_align = ''
    i = int(r)
    j = int(c)
    k = 0
    while Score[i][j] > 0:
        # waterman修改条件，到零结束
        if k < traceback_pathway_col.shape[1] - 1:
            if Go_left[tpn][k] and Go_up[tpn][k]:
                seq1_align += sequence_1[i - 1]
                seq2_align += sequence_2[j - 1]
                i -= 1
                j -= 1
            elif not (Go_left[tpn][k]) and Go_up[tpn][k]:
                seq1_align += sequence_1[i - 1]
                seq2_align += '-'
                i -= 1
            elif Go_left[tpn][k] and not (Go_up[tpn][k]):
                seq1_align += '-'
                seq2_align += sequence_2[j - 1]
                j -= 1
            k += 1
    seq1_align_set += [seq1_align[::-1]]
    seq2_align_set += [seq2_align[::-1]]
    print("下面是第{}个".format(tpn + 1))
    print(seq1_align[::-1])
    print(seq2_align[::-1])
    print(' ')
#%%
'''
下面就是得分矩阵的热图以及回溯路径（格子）画出来了
'''
import pandas as pd
import seaborn as sns
from matplotlib import pyplot as plt

Score = pd.DataFrame(Score)
row_name = list(sequence_1)
row_name.insert(0, ' ')
col_name = list(sequence_2)
col_name.insert(0, ' ')
Score.index = row_name
Score.columns = col_name
traceback_way_mat = np.ones([len(sequence_1) + 1, len(sequence_2) + 1])

for i in range(traceback_pathway_row.shape[0]):
    traceback_way_mat[traceback_pathway_row[i][:], traceback_pathway_col[i][:]] = 0
ax1 = sns.heatmap(Score, linecolor='white', linewidth=0, square=True, cmap="RdBu_r", annot=True)
plt.savefig('sw_Heatmap with annotation.png',dpi=300)
plt.show()
ax2 = sns.heatmap(Score, linecolor='white', linewidth=0, square=True, cmap="RdBu_r")
plt.savefig('sw_Heatmap.png',dpi=300)
plt.show()
ax3 = sns.heatmap(Score, linecolor='white', linewidth=0, square=True, cmap="RdBu_r", mask=traceback_way_mat)
plt.savefig('sw_Heatmap_traceback',dpi=300)
plt.show()

#%%
plt.rcParams['figure.figsize'] = (6, 6)
for j in range(traceback_pathway_col.shape[0]):
    fig = plt.figure()
    ax = plt.axes()
    plt.grid(zorder=0, linestyle='-.')
    for i in range(traceback_pathway_col.shape[1]-2):
        xs = traceback_pathway_col[j][i]
        ys = traceback_pathway_row[j][i]
        xe = traceback_pathway_col[j][i+1]
        ye = traceback_pathway_row[j][i+1]
        ax.arrow(xs, ys, xe-xs, ye-ys, length_includes_head=True,head_width=0.3, fc='crimson', ec='hotpink',zorder=10)
    ax.set_xlim(-0.5, len(col_name)-0.5)
    ax.set_ylim(-0.5, len(col_name)-0.5)
    plt.xticks(np.arange(0,len(col_name),1), col_name)
    plt.yticks(np.arange(0,len(row_name),1), row_name)
    ax.xaxis.set_ticks_position('top')
    ax.invert_yaxis()
    # ax.set_title('No.{}'.format(j+1),fontsize=12,color='k',loc='left')
    ax.set_title('No.{}'.format(j + 1), fontsize=12, color='k', loc='left', y=0.86, x=0.38, fontweight='bold')
    ax.set_title('{}{}{}'.format(seq1_align_set[j], '\n', seq2_align_set[j]), fontsize=16, fontfamily='monospace',
                 color='k', fontweight='bold', y=0.83, x=0.7)
    plt.savefig('sw_No.{}'.format(j+1)+'.png',dpi=300)
    plt.show()

import datetime
print("这是代码执行时间: ",datetime.datetime.now())
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222