• Pytorch深度学习实战（1）—— 使用LSTM 自动编码器进行时间序列异常检测

     🔎大家好，我是Sonhhxg_柒，希望你看完之后，能对你有所帮助，不足请指正！共同学习交流🔎

    📝个人主页－Sonhhxg_柒的博客_CSDN博客 📃

    🎁欢迎各位→点赞👍 + 收藏⭐️ + 留言📝​

    📣系列专栏 - 机器学习【ML】 自然语言处理【NLP】  深度学习【DL】

    ​

     🖍foreword

    ✔说明⇢本人讲解主要包括Python、机器学习（ML）、深度学习（DL）、自然语言处理（NLP）等内容。

    如果你对这个系列感兴趣的话，可以关注订阅哟👋

    文章目录

    数据

    探索性数据分析

    LSTM 自动编码器

    重建损失

    ECG 数据中的异常检测

    数据预处理

    训练

    保存模型

    选择阈值

    评估

    正常听力节拍

    异常情况

    概括

    TL;DR 使用真实世界的心电图 (ECG) 数据来检测患者心跳中的异常情况。我们将构建一个 LSTM 自动编码器，在一组正常的心跳上对其进行训练，并将看不见的示例分类为正常或异常

    在本教程中，您将学习如何使用 LSTM 自动编码器检测时间序列数据中的异常。您将使用来自单个心脏病患者的真实心电图数据来检测异常心跳。

    在本教程结束时，您将学习如何：

    • 准备数据集以从时间序列数据中进行异常检测
    • 使用 PyTorch 构建 LSTM 自动编码器
    • 训练和评估您的模型
    • 选择异常检测的阈值
    • 将看不见的示例分类为正常或异常

    数据

    该数据集包含 5,000 个时间序列示例（通过 ECG 获得），具有 140 个时间步长。每个序列对应于单个充血性心力衰竭患者的单个心跳。

    心电图（ECG 或 EKG）是一种通过测量心脏的电活动来检查心脏功能的测试。每次心跳时，都会有一个电脉冲（或电波）穿过您的心脏。这种波会导致肌肉挤压并从心脏泵出血液。资源

    我们有 5 种类型的心跳（类）：

    • 正常 (N)
    • R-on-T 室性早搏 (R-on-T PVC)
    • 室性早搏 (PVC)
    • 室上性早搏或异位搏动（SP 或 EB）
    • 未分类节拍 (UB)。

    假设一个健康的心脏和每分钟 70 到 75 次的典型心率，每个心动周期或心跳大约需要 0.8 秒才能完成一个周期。频率：每分钟 60-100 次（人类） 持续时间：0.6-1 秒（人类）来源

    该数据集在我的 Google Drive 上可用。我们去取得它：

    1. # BASH
    2. !gdown --id 16MIleqoIr1vYxlGk4GKnGmrsCPuWkkpT
    3. !unzip -qq ECG5000.zip
    device = torch.device("cuda" if torch.cuda.is_available() else "cpu")

    数据有多种格式。我们将arff文件加载到 Pandas 数据帧中：

    1. with open('ECG5000_TRAIN.arff') as f:
    2.     train = a2p.load(f)
    3. with open('ECG5000_TEST.arff') as f:
    4.     test = a2p.load(f)

    我们将把训练和测试数据合并到一个数据框中。这将为我们提供更多数据来训练我们的自动编码器。我们还将对其进行洗牌：

    1. df = train.append(test)
    2. df = df.sample(frac=1.0)
    3. df.shape
    1.  
    2. (5000, 141)

     我们有 5,000 个示例。每行代表一个心跳记录。让我们命名可能的类：

    1. CLASS_NORMAL = 1
    2. class_names = ['Normal','R on T','PVC','SP','UB']

     接下来，我们将最后一列重命名为target，以便更容易引用它：

    1. new_columns = list(df.columns)
    2. new_columns[-1] = 'target'
    3. df.columns = new_columns

    探索性数据分析

    让我们检查一下每个心跳类有多少个示例：

    df.target.value_counts()

     Output:

    1. 1    2919
    2. 2    1767
    3. 4     194
    4. 3      96
    5. 5      24
    6. Name: target, dtype: int64

    让我们绘制结果： 

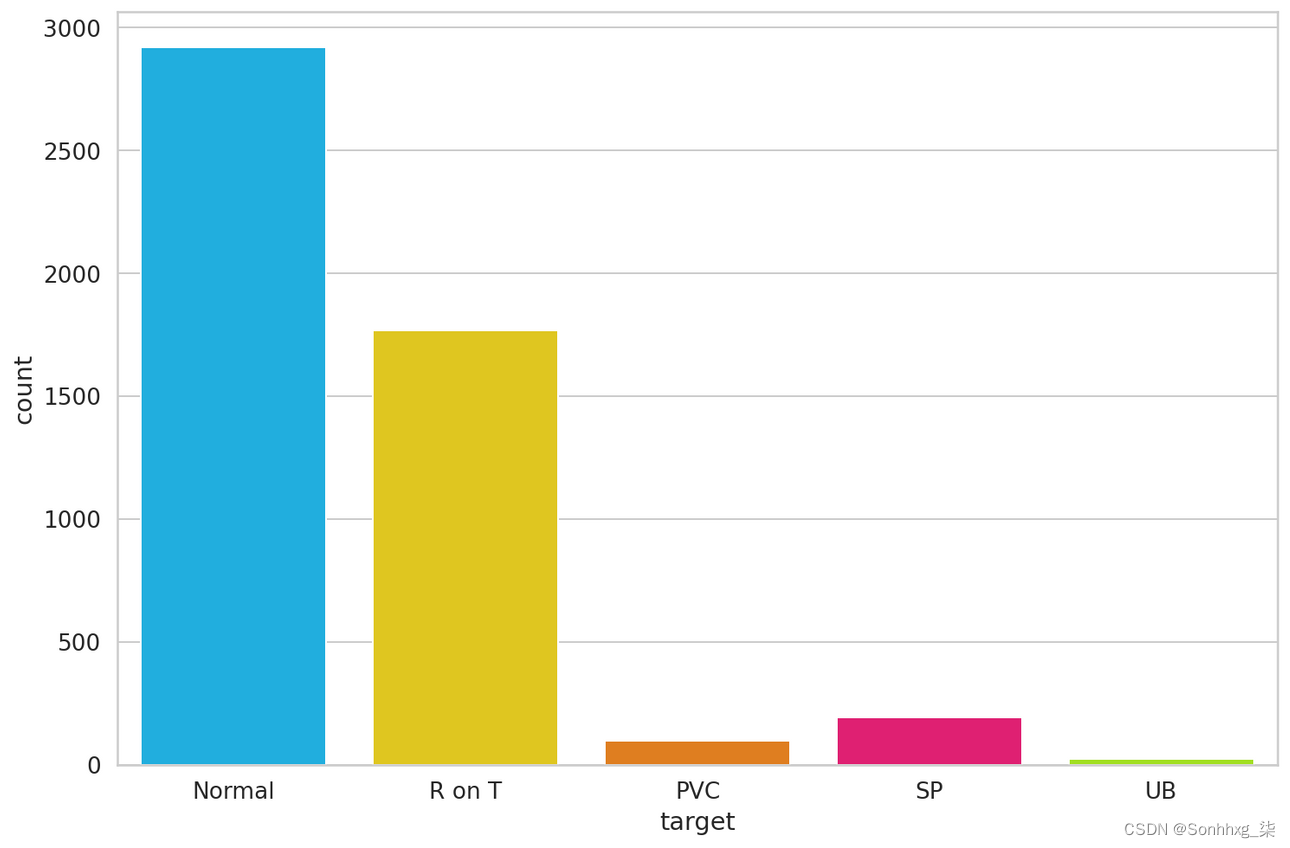
         到目前为止，普通班的例子最多。这很棒，因为我们将使用它来训练我们的模型。

    让我们看一下每个类的平均时间序列（在顶部和底部用一个标准偏差平滑）：

    正常类与所有其他类具有明显不同的模式，这是非常好的。也许我们的模型将能够检测到异常？

    LSTM 自动编码器

    自动编码器的工作是获取一些输入数据，将其传递给模型，并获得输入的重构。重建应该尽可能匹配输入。诀窍是使用少量参数，以便您的模型学习数据的压缩表示。

    从某种意义上说，自动编码器试图只学习数据最重要的特征（压缩版本）。在这里，我们将了解如何将时间序列数据提供给自动编码器。我们将使用几个 LSTM 层（因此是 LSTM 自动编码器）来捕获数据的时间依赖性。

    要将序列分类为正常或异常，我们将选择一个阈值，超过该阈值时心跳被视为异常。

    重建损失

    在训练自动编码器时，目标是尽可能地重构输入。这是通过最小化损失函数来完成的（就像在监督学习中一样）。这个函数被称为重建损失。交叉熵损失和均方误差是常见的例子。

    ECG 数据中的异常检测

    我们将使用正常的心跳作为模型的训练数据并记录重建损失。但首先，我们需要准备数据：

    数据预处理

    让我们获取所有正常的心跳并删除目标（类）列：

    1. normal_df = df[df.target == str(CLASS_NORMAL)].drop(labels='target', axis=1)
    2. normal_df.shape

    (2919, 140)

     我们将合并所有其他类并将它们标记为异常：

    1. anomaly_df = df[df.target != str(CLASS_NORMAL)].drop(labels='target', axis=1)
    2. anomaly_df.shape

     (2081, 140)

    我们将正常示例拆分为训练集、验证集和测试集：

    1. train_df, val_df = train_test_split(
    2.     normal_df,
    3.     test_size=0.15,
    4.     random_state=RANDOM_SEED
    5. )
    6. val_df, test_df = train_test_split(
    7.     val_df,
    8.     test_size=0.33,
    9.     random_state=RANDOM_SEED
    10. )

    我们需要将我们的示例转换为张量，以便我们可以使用它们来训练我们的自动编码器。让我们为此编写一个辅助函数：

    1. def create_dataset(df):
    2.     sequences = df.astype(np.float32).to_numpy().tolist()
    3.     dataset = [torch.tensor(s).unsqueeze(1).float() for s in sequences]
    4.     n_seq, seq_len, n_features = torch.stack(dataset).shape
    5.     return dataset, seq_len, n_features

    每个时间序列都将转换为形状序列长度x特征数（在我们的例子中为 140x1）的 2D 张量。

    让我们创建一些数据集：

    1. train_dataset, seq_len, n_features = create_dataset(train_df)
    2. val_dataset, _, _ = create_dataset(val_df)
    3. test_normal_dataset, _, _ = create_dataset(test_df)
    4. test_anomaly_dataset, _, _ = create_dataset(anomaly_df)

     LSTM 自动编码器

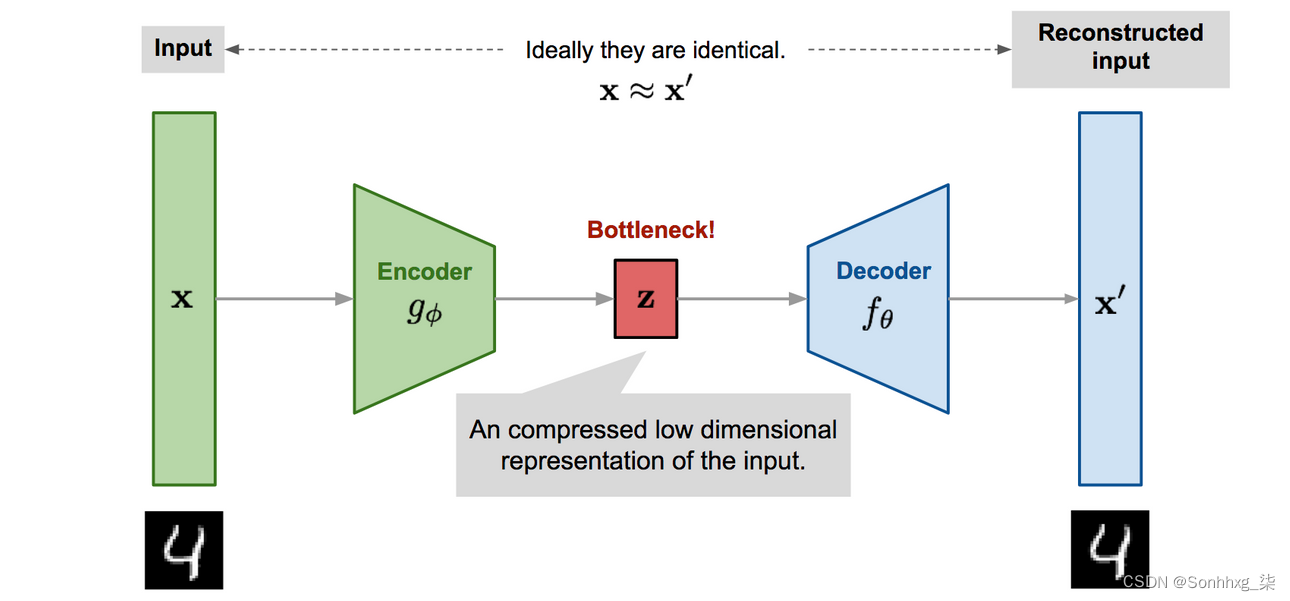
                                                                            自动编码器 

    示例自动编码器架构图像源

    通用的自动编码器架构由两个组件组成。一个压缩输入的编码器和一个尝试重建它的解码器。

    我们将使用来自这个GitHub存储库的 LSTM 自动编码器，并进行一些小的调整。我们模型的工作是重建时间序列数据。让我们从编码器开始：

    1. class Encoder(nn.Module):
    2.     def __init__(self, seq_len, n_features, embedding_dim=64):
    3.         super(Encoder, self).__init__()
    4.         self.seq_len, self.n_features = seq_len, n_features
    5.         self.embedding_dim, self.hidden_dim = embedding_dim, 2 * embedding_dim
    6.         self.rnn1 = nn.LSTM(
    7.             input_size=n_features,
    8.             hidden_size=self.hidden_dim,
    9.             num_layers=1,
    10.             batch_first=True
    11.         )
    12.         self.rnn2 = nn.LSTM(
    13.             input_size=self.hidden_dim,
    14.             hidden_size=embedding_dim,
    15.             num_layers=1,
    16.             batch_first=True
    17.         )
    18.     def forward(self, x):
    19.         x = x.reshape((1, self.seq_len, self.n_features))
    20.         x, (_, _) = self.rnn1(x)
    21.         x, (hidden_n, _) = self.rnn2(x)
    22.         return hidden_n.reshape((self.n_features, self.embedding_dim))

    编码器使用两个 LSTM 层来压缩时间序列数据输入。

    接下来，我们将使用解码器对压缩表示进行解码：

    1. class Decoder(nn.Module):
    2.     def __init__(self, seq_len, input_dim=64, n_features=1):
    3.         super(Decoder, self).__init__()
    4.         self.seq_len, self.input_dim = seq_len, input_dim
    5.         self.hidden_dim, self.n_features = 2 * input_dim, n_features
    6.         self.rnn1 = nn.LSTM(
    7.             input_size=input_dim,
    8.             hidden_size=input_dim,
    9.             num_layers=1,
    10.             batch_first=True
    11.         )
    12.         self.rnn2 = nn.LSTM(
    13.             input_size=input_dim,
    14.             hidden_size=self.hidden_dim,
    15.             num_layers=1,
    16.             batch_first=True
    17.         )
    18.         self.output_layer = nn.Linear(self.hidden_dim, n_features)
    19.     def forward(self, x):
    20.         x = x.repeat(self.seq_len, self.n_features)
    21.         x = x.reshape((self.n_features, self.seq_len, self.input_dim))
    22.         x, (hidden_n, cell_n) = self.rnn1(x)
    23.         x, (hidden_n, cell_n) = self.rnn2(x)
    24.         x = x.reshape((self.seq_len, self.hidden_dim))
    25.         return self.output_layer(x)

    我们的解码器包含两个 LSTM 层和一个提供最终重建的输出层。

    是时候将所有内容包装到一个易于使用的模块中了：

    1. class RecurrentAutoencoder(nn.Module):
    2.     def __init__(self, seq_len, n_features, embedding_dim=64):
    3.         super(RecurrentAutoencoder, self).__init__()
    4.         self.encoder = Encoder(seq_len, n_features, embedding_dim).to(device)
    5.         self.decoder = Decoder(seq_len, embedding_dim, n_features).to(device)
    6.     def forward(self, x):
    7.         x = self.encoder(x)
    8.         x = self.decoder(x)
    9.         return x

    我们的自动编码器通过编码器和解码器传递输入。让我们创建它的一个实例：

    1. model = RecurrentAutoencoder(seq_len, n_features, 128)
    2. model = model.to(device)

    训练

    让我们为我们的训练过程编写一个辅助函数：

    1. def train_model(model, train_dataset, val_dataset, n_epochs):
    2.     optimizer = torch.optim.Adam(model.parameters(), lr=1e-3)
    3.     criterion = nn.L1Loss(reduction='sum').to(device)
    4.     history = dict(train=[], val=[])
    5.     best_model_wts = copy.deepcopy(model.state_dict())
    6.     best_loss = 10000.0
    7.     for epoch in range(1, n_epochs + 1):
    8.         model = model.train()
    9.         train_losses = []
    10.         for seq_true in train_dataset:
    11.             optimizer.zero_grad()
    12.             seq_true = seq_true.to(device)
    13.             seq_pred = model(seq_true)
    14.             loss = criterion(seq_pred, seq_true)
    15.             loss.backward()
    16.             optimizer.step()
    17.             train_losses.append(loss.item())
    18.         val_losses = []
    19.         model = model.eval()
    20.         with torch.no_grad():
    21.             for seq_true in val_dataset:
    22.                 seq_true = seq_true.to(device)
    23.                 seq_pred = model(seq_true)
    24.                 loss = criterion(seq_pred, seq_true)
    25.                 val_losses.append(loss.item())
    26.         train_loss = np.mean(train_losses)
    27.         val_loss = np.mean(val_losses)
    28.         history['train'].append(train_loss)
    29.         history['val'].append(val_loss)
    30.         if val_loss < best_loss:
    31.             best_loss = val_loss
    32.             best_model_wts = copy.deepcopy(model.state_dict())
    33.         print(f'Epoch {epoch}: train loss {train_loss} val loss {val_loss}')
    34.     model.load_state_dict(best_model_wts)
    35.     return model.eval(), history

     在每个时期，训练过程都会为我们的模型提供所有训练示例，并评估验证集的性能。请注意，我们使用的批量大小为 1（我们的模型一次只能看到 1 个序列）。我们还记录了过程中的训练和验证集损失。

    请注意，我们正在最小化L1Loss，它测量 MAE（平均绝对误差）。为什么？重建似乎比 MSE（均方误差）更好。

    我们将获得具有最小验证错误的模型版本。让我们做一些训练：

    1. model, history = train_model(
    2.     model,
    3.     train_dataset,
    4.     val_dataset,
    5.     n_epochs=150
    6. )

     我们的模型收敛得很好。似乎我们可能需要一个更大的验证集来平滑结果，但现在就可以了。

    保存模型

    让我们存储模型以备后用：

    1. MODEL_PATH = 'model.pth'
    2. torch.save(model, MODEL_PATH)

     如果要下载并加载预训练模型，请取消注释下一行：

    1. # !gdown --id 1jEYx5wGsb7Ix8cZAw3l5p5pOwHs3_I9A
    2. # model = torch.load('model.pth')
    3. # model = model.to(device)

    选择阈值

    有了我们手头的模型，我们可以看看训练集上的重建误差。让我们首先编写一个辅助函数来从我们的模型中获取预测：

    1. def predict(model, dataset):
    2.     predictions, losses = [], []
    3.     criterion = nn.L1Loss(reduction='sum').to(device)
    4.     with torch.no_grad():
    5.         model = model.eval()
    6.         for seq_true in dataset:
    7.             seq_true = seq_true.to(device)
    8.             seq_pred = model(seq_true)
    9.             loss = criterion(seq_pred, seq_true)
    10.             predictions.append(seq_pred.cpu().numpy().flatten())
    11.             losses.append(loss.item())
    12.     return predictions, losses

    我们的函数遍历数据集中的每个示例并记录预测和损失。让我们得到损失并看看它们：

    1. _, losses = predict(model, train_dataset)
    2. sns.distplot(losses, bins=50, kde=True);
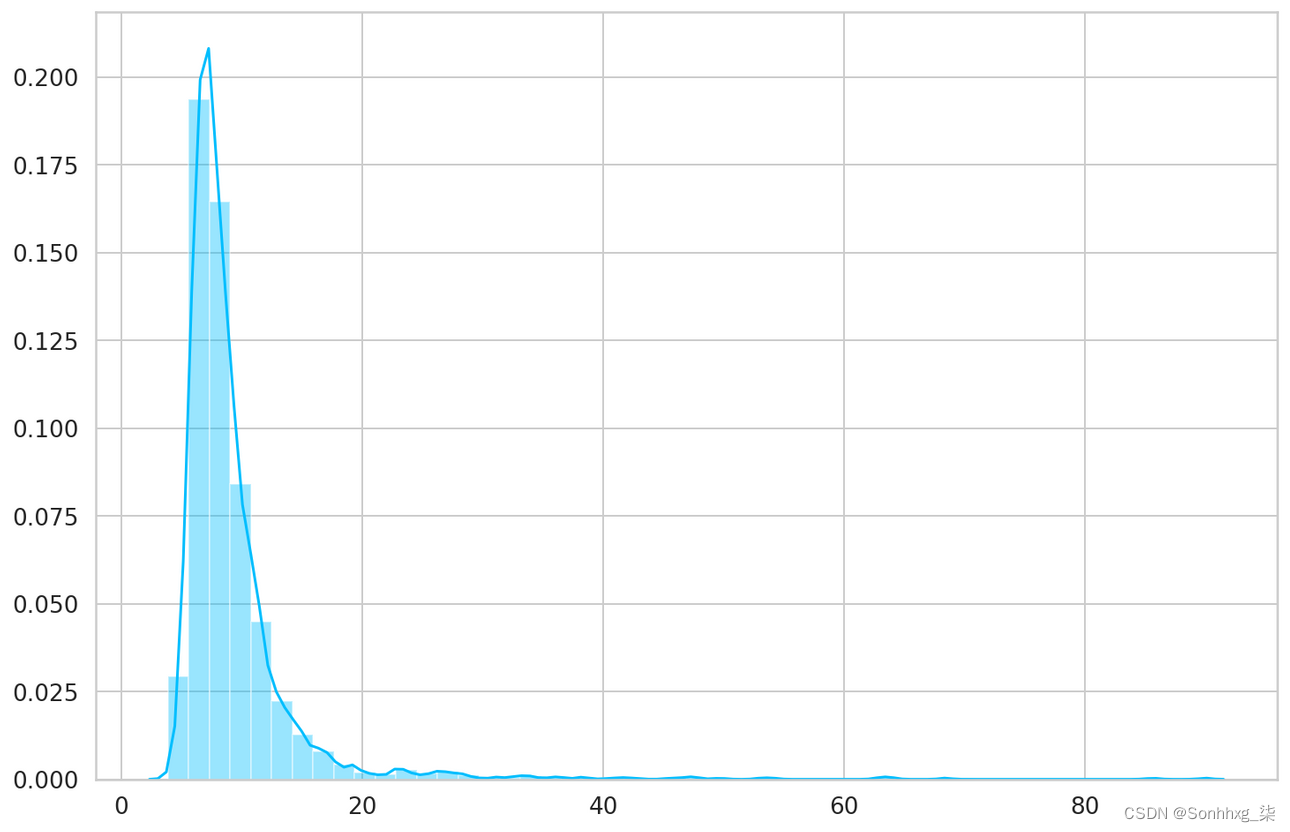
    THRESHOLD = 26

    评估

    使用阈值，我们可以将问题转化为简单的二元分类任务：

    • 如果示例的重建损失低于阈值，我们会将其归类为正常心跳
    • 或者，如果损失高于阈值，我们会将其归类为异常

    正常听力节拍

    让我们检查一下我们的模型在正常心跳上的表现如何。我们将使用测试集中的正常心跳（我们的模型没有看到这些）：

    1. predictions, pred_losses = predict(model, test_normal_dataset)
    2. sns.distplot(pred_losses, bins=50, kde=True);


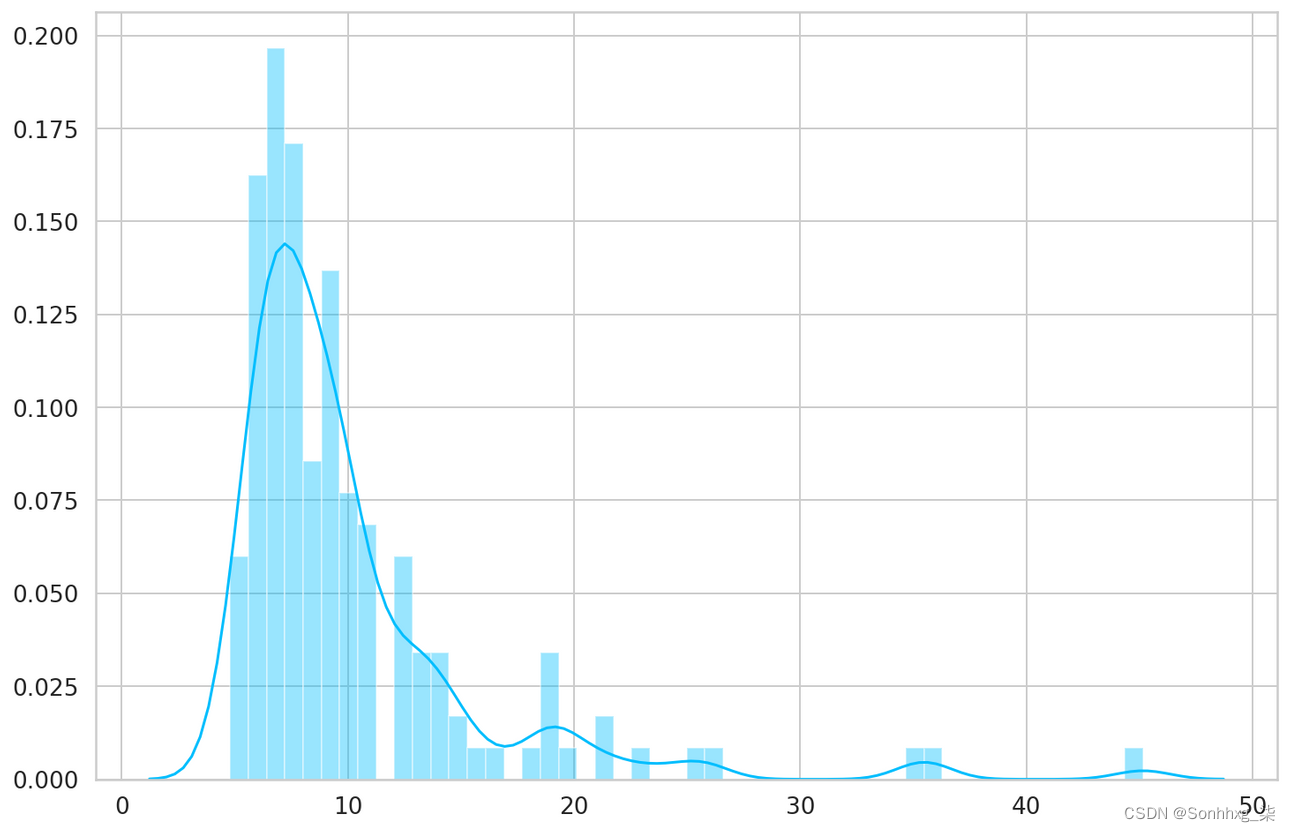
     我们将计算正确的预测：

    1. correct = sum(l <= THRESHOLD for l in pred_losses)
    2. print(f'Correct normal predictions: {correct}/{len(test_normal_dataset)}')

    Correct normal predictions: 142/145 

    异常情况

    我们将对异常示例执行相同的操作，但它们的数量要高得多。我们将得到一个与正常心跳大小相同的子集：

    anomaly_dataset = test_anomaly_dataset[:len(test_normal_dataset)]

     现在我们可以对异常子集的模型进行预测：

    1. predictions, pred_losses = predict(model, anomaly_dataset)
    2. sns.distplot(pred_losses, bins=50, kde=True);

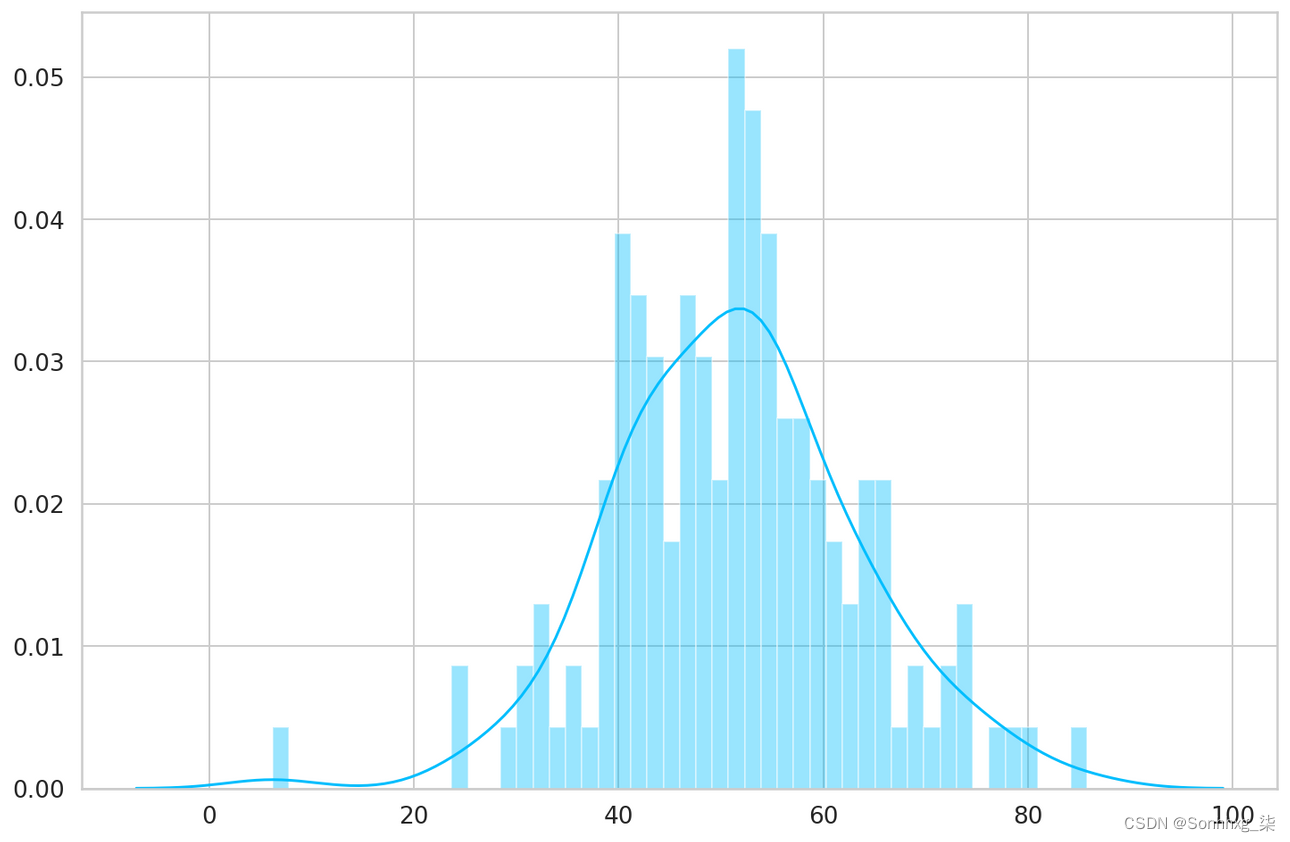
     最后，我们可以统计超过阈值的示例数量（视为异常）： 

    1. correct = sum(l > THRESHOLD for l in pred_losses)
    2. print(f'Correct anomaly predictions: {correct}/{len(anomaly_dataset)}')

     Correct anomaly predictions: 142/145 

    我们取得了非常好的结果。在现实世界中，您可以根据要容忍的错误类型来调整阈值。在这种情况下，您可能希望误报（正常心跳被视为异常）多于误报（异常被视为正常）。

    看例子

    我们可以叠加真实的和重建的时间序列值，看看它们有多接近。我们将针对一些正常和异常情况执行此操作：

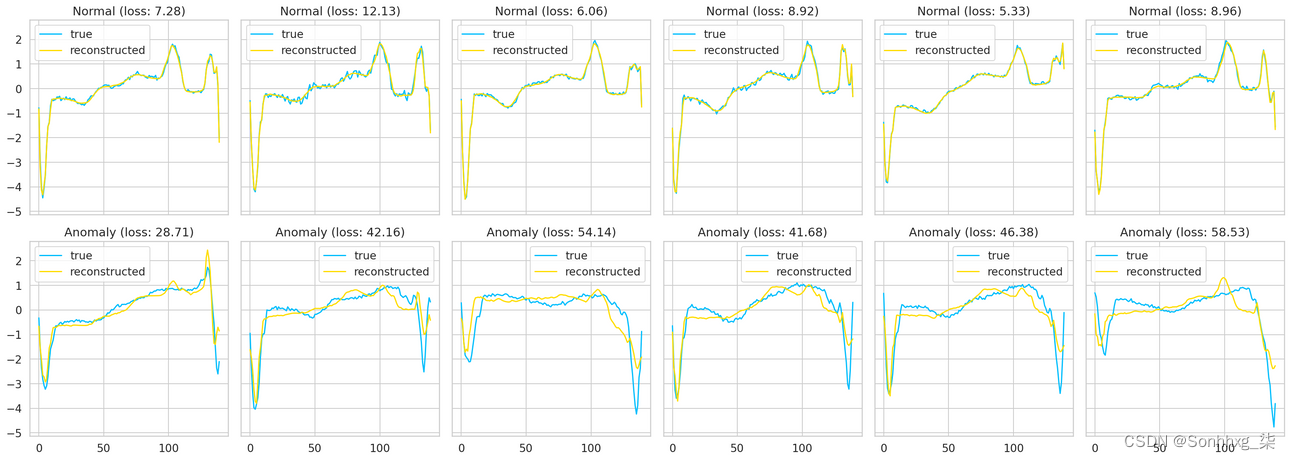
    概括

    在本教程中，您学习了如何使用 PyTorch 创建 LSTM 自动编码器，并使用它来检测 ECG 数据中的心跳异常。

    你学会了如何：

    • 准备数据集以从时间序列数据中进行异常检测
    • 使用 PyTorch 构建 LSTM 自动编码器
    • 训练和评估您的模型
    • 选择异常检测的阈值
    • 将看不见的示例分类为正常或异常

    虽然我们的时间序列数据是单变量的（我们只有 1 个特征），但代码应该适用于多变量数据集（多个特征），几乎不需要修改。随意尝试！

  • 相关阅读:
    Pytorch：张量的索引操作
    关于websocket做即时通信功能
    linux下.bashrc文件修改和生效
    Git学习笔记2
    PHP 在线学习平台系统mysql数据库web结构layUI布局apache计算机软件工程网页wamp
    MongoDB文档（二）
    Scala 的安装与使用
    盐酸左氧氟沙星修饰牛血清白蛋白，OFLX-BSA，bovine serum albumin-OFLX
    实战项目: 负载均衡
    7. RabbitMQ之延时队列
  • 原文地址：https://blog.csdn.net/sikh_0529/article/details/127818626