滑动窗口分位数#
分位数计算公式#
分位数的计算公式有PERCETILE.INC和PERCENTILE.EXC两种,两个公式的计算逻辑是完全一样的,仅仅取数的范围大小不一样,这里我们使用PERTILE.INC来完成分位数的计算,具体的分位数计算逻辑不是本文的重点,这里就不赘述了。
分位数的题目要求#
给你一个数组 List
由于在具体的业务中,每一条数据除了数值以外,还有其他的业务属性,所以我在此顶一个了一个计算使用的抽象类PercentilePriorityQueueElement,仅有需要计算的值,而Element是自定义的业务元素对象,可以包含具体的业务属性。
PercentilePriorityQueueElement类如下
public abstract static class PercentilePriorityQueueElement implements Comparable<PercentilePriorityQueueElement> {
private final long id;
private final double value;
protected PercentilePriorityQueueElement(double value) {
this.id = IdWorker.getId();
this.value = value;
}
/**
* 获取计算值
*
* @return double
*/
public double getValue() {
return this.value;
}
Element类如下
class Element extends PercentileFinder.PercentilePriorityQueueElement {
Element(double v) {
super(v);
}
}
分位数计算思考#
我们首先思考一下计算分位数需要做那些事情
-
序:我们都知道,PERCENTILE.INC计算需要两个参数,一个是需要计算的元素的数组elements,另一个是百分位数percent,这里我们用取值范围为[0,1]的小数来表示。
-
1:初始时,我们需要将数组elements的前windowSize个元素放入滑动窗口中,然后对所有的这些元素排序
-
2:找出两个分为点所在的位置,(windowSize−1)∗p=i+j (其中windowSize为数组元素的个数,也即是窗口大小,将计算结果的整数部分用i表示,小数部分用j来表示,p是百分位数,如90%的话就是0.9)
-
3:找出这些元素的两个分位点元素smallElement和largeElement,其中smallElement是大于等于所有左边的元素,largeElement是小于等于所有右边的元素。
-
4:ans=(1−j)∗elements[i]+j∗elements[i+1] (ans就是我们所需要的百分位数)
-
5: 移除窗口的第一个元素,将一个新的元素放入窗口中,重复上述步骤
用图表示的话,其中smallElement和largeElement的位置就是如下图所示的位置
滑动窗口分位数的算法设计#
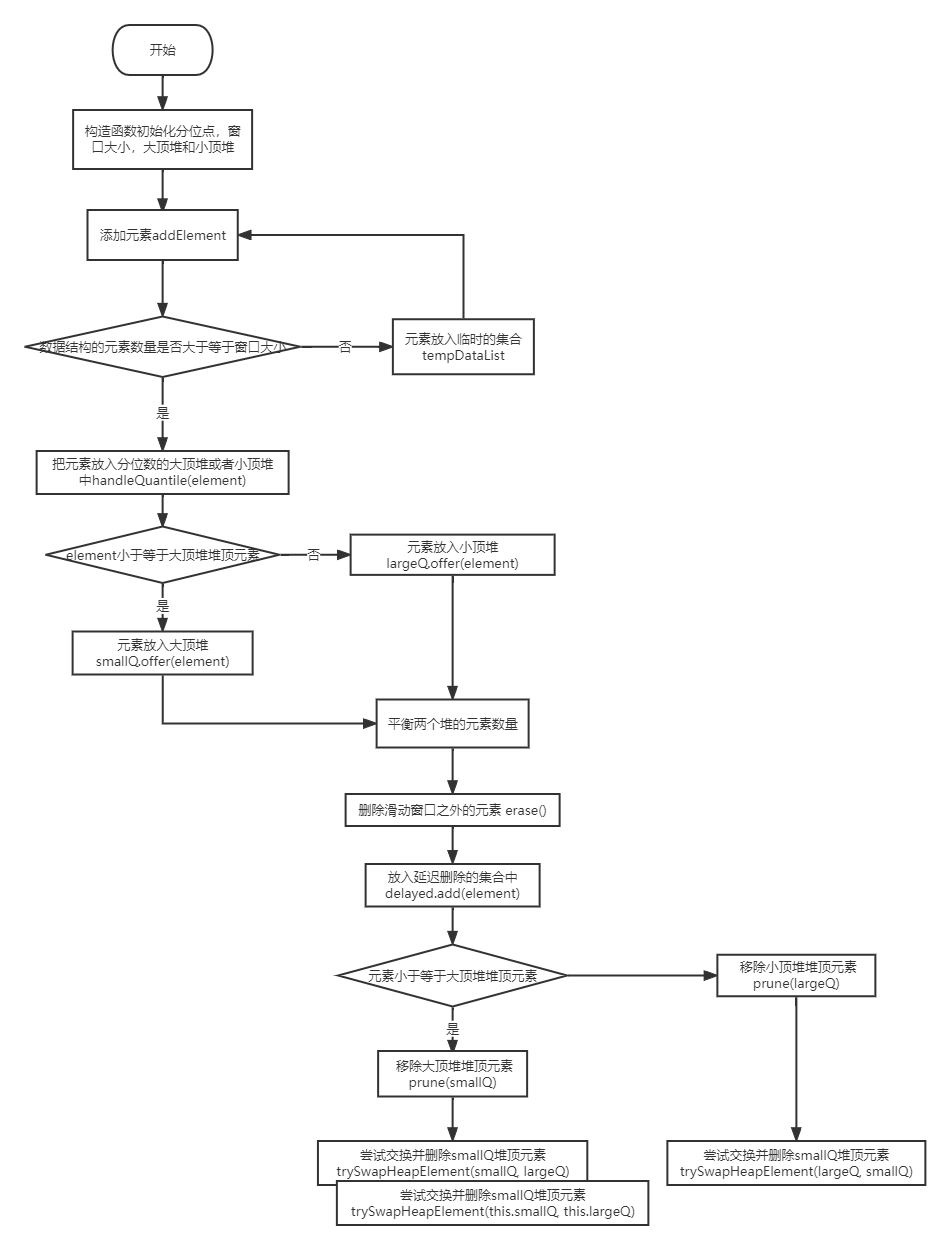
考虑到我们是使用滑动窗口计算的分位数,则必然包含一下三个过程
-
1:向滑动窗口中放入数据
-
2:将滑动的首元素移除出窗口
-
3:计算窗口的分位数
根据以上三个过程,我们设计出三个接口,如下:
public void addElement(E element);//将一个元素加入数据结构
private void erase(E element);//将一个元素移除数据结构
public Double getPercentInc();//计算分位数
-
1:根据以上对分位数计算的思考,我们考虑设计一个计算分位数的数据结构,考虑到smallElement元素左边的元素都小于等于smallElement,而largeElement元素右边的元素都大于等于largeElement,我们可以使用两个堆来保证这一要求,其中smallElement元素及其左边的元素使用一个大顶堆,而largeElement及其右边的元素使用一个小顶堆,这样就可以满足我们的要求。
-
2:堆数据结构的缺点
-
2.1:考虑到堆这一数据结构的设计不支持删除非堆顶元素,即使Java的PriorityQueue提供了remove()方法来移除非堆顶元素,调用removeAt()也能保证堆这一数据结构的要求,但是其remove的时候调用的indexOf()方法为线性查找,其复杂度为O(n),n为窗口大小,所以相对来说复杂度还是很高的,这就违背了我们这一数据结构的初衷。(如果调用PriorityQueue的remove方法不如我们使用冒泡排序中的一次冒泡更加高效,因为移除窗口的第一个元素之后整体还是有序的,所以加入元素的时候最多需要一个遍历就可以满足我们的要求,复杂度也是O(n),n为窗口大小)。
-
2.2:我们再仔细思考一下整个流程,发现如果一个元素在窗口的之外,但是该元素不在堆顶的时候,它并不影响我们的计算,因为我们的计算仅需要两个堆顶的元素,所以我们可以不立即删除该元素,等到该元素到达之后,再将该元素移除出堆中。所以我们还需要一个集合来保存这些元素,我们称删除这些元素的设计为延迟删除。
-
-
3:由于我们在加入元素的时候可能会破坏大顶堆SmallQ和小顶堆LargeQ的数量,所以我们需要在每一次加入元素之后,需要平衡两个堆中元素的数量以保证两个堆中的元素的数量始终是我们的需要的数量。
-
4:当我们加入元素的时候,我们需要根据加入元素的大小判断该元素是要放入大顶堆还是小顶堆中,由于加入元素会破坏堆中元素的数量,所以我们需要线调整元素的位置,因此我们设计一个平衡函数makeBalance()用于调整大顶堆和小顶堆的数据,调整之后,数据多出的堆由于延迟删除的原因堆顶元素有可能不是窗口之内的元素,所以我们设计一个辅助函数prune(heap)用于删除不在窗口之内的堆顶元素。由于两个堆顶的元素交换的原因,所以当两个元素的值相同的时候,可能会出现我们需要删除的元素在小顶堆,但是该元素在大顶堆中,于是我们设计一个尝试交换并删除待删除元素的函数trySwapHeapElement(PriorityQueue
opsHeap, PriorityQueue 以帮助我们解决在调整两个堆顶元素相同的时候会出现的问题。willRemoveHeap)
完整代码
import com.baomidou.mybatisplus.core.toolkit.IdWorker;
import lombok.EqualsAndHashCode;
import javax.annotation.Nullable;
import java.util.*;
import java.util.stream.Collectors;
/**
* 分位数计算
* formula: PERCENTILE.INC
*
* @author philosophy
*/
public class PercentileFinder<E extends PercentileFinder.PercentilePriorityQueueElement> {
private static final double MAX_PERCENT = 1.00;
private static final double MIN_PERCENT = 0.00;
/**
* 滑动窗口大小
*/
private final int slidingWindowSize;
/**
* 延迟删除的元素集合
*/
private final Set<E> delayed;
/**
* 待删除元素的队列
*/
private final Queue<E> todoRemoveQueue;
/**
* 大于 {分位数} 的优先级队列
*/
private final PriorityQueue<E> smallQ;
/**
* 大于 {分位数} 的优先级队列
*/
private final PriorityQueue<E> largeQ;
/**
* {smallQ}的最大数量
*/
private final int smallQueueMaxSize;
/**
* {largeQ}的最大数量
*/
private final int largeQueueMaxSize;
/**
* {largeQ}的元素数量
*/
private int largeQueueSize;
/**
* {smallQ}的元素数量
*/
private int smallQueueSize;
/**
* 分为数比例(用小数标识) 取值范围 [0,1]
*/
private double quantileScale;
/**
* 当数据总数小于窗口大小时,临时存储数据
*/
private List<E> tempDataList;
private boolean flag = false;
/**
* 分位数计算
*
* @param windowSize windowSize
* @param percent percent
*/
public PercentileFinder(int windowSize, double percent) {
check(windowSize, percent);
this.slidingWindowSize = windowSize;
//初始化分位点