15 计专

数据结构

第一题 树的非递归后序遍历

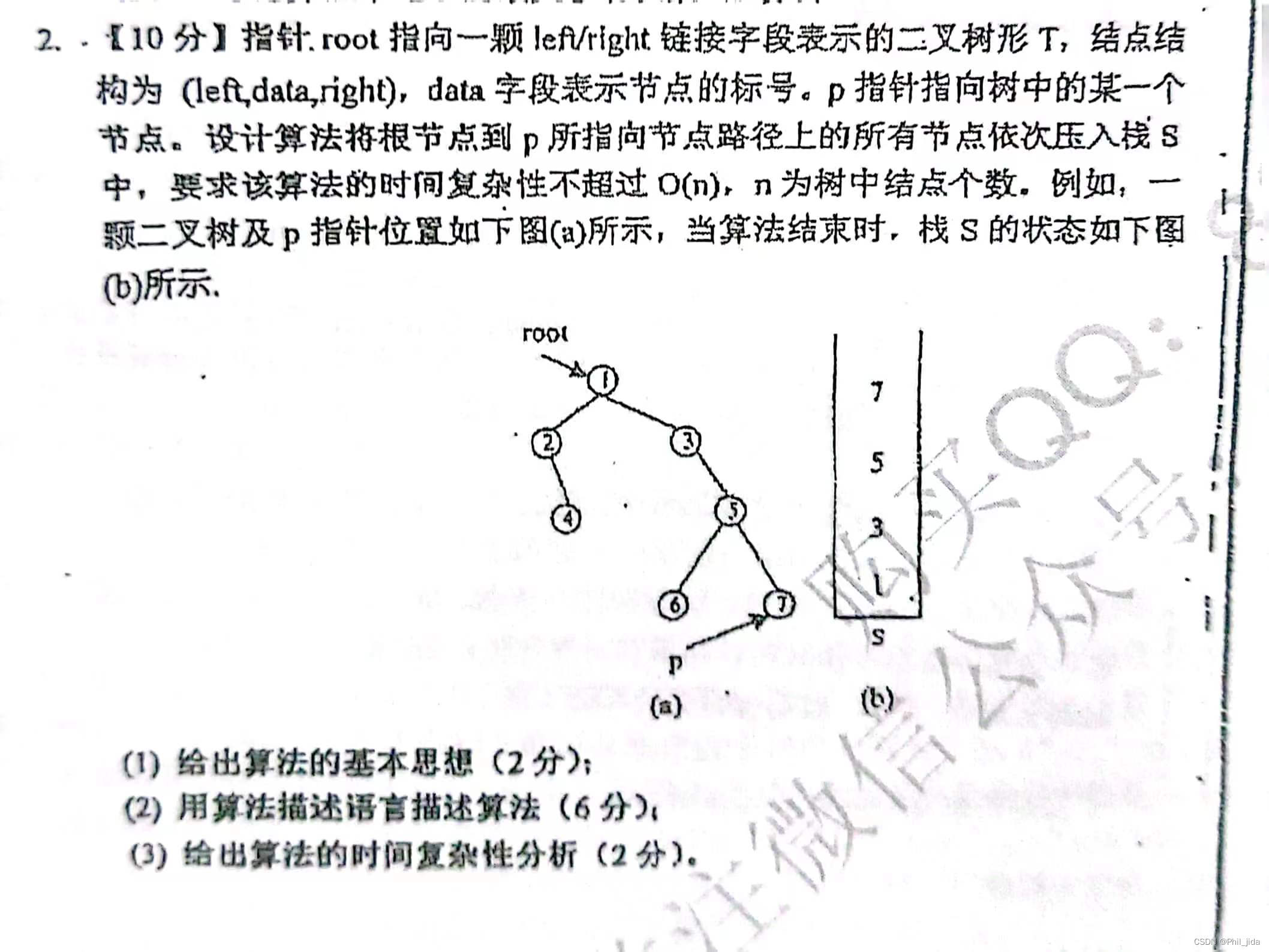
思路：

• 后序非递归实现遍历算法，当遍历到需要找到的节点时，当前栈中保存的元素就是该节点的根节点

• 具体思路，遍历左子树一直入栈，为空时取栈顶元素，但不出栈，判断是否访问过，未访问则继续访问，访问过则出栈，判断是否与需要找的节点值相同，相同的话，则跳出循环，不同的话，继续访问，保存现在访问节点，当前节点置为空，方便后面继续出栈

• 递归实现：参数中传入top，stack，在访问时不断入栈，找到了则返回，则在左右子树找，左右子树均未找到，则出栈

代码：

//数的后序遍历保存某个节点的根节点

typedef struct tnode{
	int data;
	struct tnode *left, *right;
}*tree; 

void findroot(tree root, tree stack[], struct tnode *q){//二叉树的后序遍历 
	int top = -1;
	tree p = root,r; 					//r保存之前的一个节点
	
	while(p != NULL || top != -1){
		if(p){							//不断访问左子树并入栈 
			stack[++top] = p;
			p = p->left;
		}
		else{
			p = stack[top];			//取栈顶元素 
			if(p->right != NULL && p != r){	//右子树未被访问过 
				p = p->right; 
			}
			else{						//已经访问过 
				if(p == q){				//如果是要找的节点，直接break 
					break; 
				}
				top--;				//已经访问过，不用继续访问 
				r = p;				//r指向之前访问过的节点 
				p = NULL;			//已经访问过，直接访问下一个节点 
			}
		} 
	}
}
//非递归实现
void postOrder(tree root, tree p, tree stack[], int top){
	if(root){
		stack[++top] = root;
		if(root == p){
			return;
		}
		else{
			postOrder(root->left,p, stack,top);
			postOrder(root->right,p,stack,top);
			stack[top--];
		}
	}
} 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46

程序设计

第一题

利用公式sin(X) = 1到n的求和 (-1)^ n * x^(2n+1)/(2n+1)!,编写一个求正弦函数近似值的函数，结果精确到10-5，不允许调用任何库函数

思路：

• 实现不难，但是自己多写了两个函数，答案的结果比较好，利用上一次的结果继续用，少了很多不必要的运算

代码：

double abs(double n){
	if(n > 0 ) return n;
	else return -n;
}

double sinx(double x){
	double ans = 0,temp = x,n = 1;
	while(abs(temp) > 1e-5){
		ans += temp;
		temp *= -1.0*x*x/((2*n)*(2*n+1.0)); 
		n++;
	}
	return ans;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14