毫米波雷达基础知识系列——FFT

毫米波雷达基础知识系列——FFT及DSP优化实现

FFT来源
FFT为什么快
FFT的种类
基2FFT推导

FFT来源

FFT来源于DFT离散傅里叶变换，DFT的计算公式为：
$\sum_{n=0}^{N-1} x(n)W_{N}^{kn}$
为什么不直接用DFT计算，而要用FFT的原因在于根据上面的公式计算量会很大。
我们以N等于5为例实际计算一下：

\begin{matrix} X (0) = x (0) \times W_{5}^{0} + x (1) \times W_{5}^{0} + x (2) \times W_{5}^{0} + x (3) \times W_{5}^{0} + x (4) \times W_{5}^{0} \\ X (1) = x (0) \times W_{5}^{0} + x (1) \times W_{5}^{1} + x (2) \times W_{5}^{2} + x (3) \times W_{5}^{3} + x (4) \times W_{5}^{4} \\ . . . \end{matrix}

X (0) = x (0) \times W_{5}^{0} + x (1) \times W_{5}^{0} + x (2) \times W_{5}^{0} + x (3) \times W_{5}^{0} + x (4) \times W_{5}^{0} X (1) = x (0) \times W_{5}^{0} + x (1) \times W_{5}^{1} + x (2) \times W_{5}^{2} + x (3) \times W_{5}^{3} + x (4) \times W_{5}^{4} . . .

可以看出来，每算一个X(k)就要计算5次乘法和4次加法，对于计算机来说，乘法运算要比加法运算耗时且更耗资源。也就是说，根据DFT完成一次完整的运算要进行N的2次方次乘法运算，N越大，计算就越困难。FFT能够明显降低运算次数，因此工程中不使用DFT，而用FFT进行计算。

FFT为什么快

FFT利用了旋转因子的周期性和特殊性，避免了一些不必要的运算，因此FFT执行起来比较快。旋转因子
$W_{N}^{k n}=e^{-j(2 \pi / N) k n} \text { 是旋转因子 }$

FFT的种类

常规的FFT按基分类可以分为基2-FFT、基4-FFT、混合基FFT。一般来讲，基2FFT适用于采样序列的个数是2的N次方的情况，同理基4FFT适用于采样序列的个数是4的N次方的情况，基4FFT的速度要比基2FFT更快。混合基FFT是先用基4FFT处理前4的N次方个数据在处理后面2的N次方的数据。

基2FFT推导

基 2 FFT 算法利用了旋转因子的以下周期性特性。

\begin{array}{l} W_{N}^{0} = e^{- j (2 π / N) 0} = e^{- j (0)} = \cos (0) + j \sin (0) = 1 \\ W_{N}^{k N / 2} = e^{- j (2 π / N) k N / 2} = e^{- j (π k)} = (\cos (- π) + j \sin (- π))^{k} = (- 1)^{k} \\ W_{N}^{2 k n} = e^{- j (2 π / N) 2 k n} = e^{- j (2 π / (N / 2)) k n} = W_{N / 2}^{k n} \end{array}

W_{N}^{0} = e^{- j (2 π / N) 0} = e^{- j (0)} = cos (0) + j sin (0) = 1 W_{N}^{k N / 2} = e^{- j (2 π / N) k N / 2} = e^{- j (π k)} = (cos (- π) + j sin (- π))^{k} = (- 1)^{k} W_{N}^{2 k n} = e^{- j (2 π / N) 2 k n} = e^{- j (2 π / (N / 2)) k n} = W_{N / 2}^{k n}

利用这些特性，可以把 N 点 DFT 分解为以下两个 N/2 点 DFT

\begin{aligned} X (k) & = \sum_{n = 0}^{N - 1} x (n) W_{N}^{n k} = \sum_{n = 0}^{N / 2 - 1} x (n) W_{N}^{n k} + \sum_{n = N / 2}^{N - 1} x (n) W_{N}^{n k} \\ = \sum_{n = 0}^{N / 2 - 1} [x (n) W_{N}^{n k} + x (n + N / 2) W_{N}^{(n + N / 2) k}] \\ = \sum_{n = 0}^{N / 2 - 1} [x (n) W_{N}^{n k} + x (n + N / 2) W_{N}^{k N / 2} W_{N}^{n k}] \\ = \sum_{n = 0}^{N / 2 - 1} [x (n) W_{N}^{n k} + (- 1)^{k} x (n + N / 2) W_{N}^{n k}] \\ = \sum_{n = 0}^{N / 2 - 1} [x (n) + (- 1)^{k} x (n + N / 2)] W_{N}^{n k} \end{aligned}

让我们把输出序列 X(k), k= 0,…, N-1 分解成两个序列：
偶数序列和奇数序列
其中偶数序列X(2r)，r=0,…,N/2-1

\begin{aligned} X (2 r) & = \sum_{n = 0}^{N / 2 - 1} [x (n) + (- 1)^{2 r} x (n + N / 2)] W_{N}^{2 n r} \\ = \sum_{n = 0}^{N / 2 - 1} [x (n) + x (n + N / 2)] W_{N}^{2 n r} \\ = \sum_{n = 0}^{N / 2 - 1} [x (n) + x (n + N / 2)] W_{N / 2}^{n r} \\ = D F T_{N / 2} (x (n) + x (n + N / 2)) \end{aligned}

基数序列X(2r+1)，r=0,…N/2-1

\begin{aligned} X (2 r + 1) & = \sum_{n = 0}^{N / 2 - 1} [x (n) + (- 1)^{(2 r + 1)} x (n + N / 2)] W_{N}^{n^{*} (2 r + 1)} \\ = \sum_{n = 0}^{N / 2 - 1} [x (n) - x (n + N / 2)] W_{N}^{n} W_{N}^{2 n r} \\ = \sum_{n = 0}^{N / 2 - 1} {[x (n) - x (n + N / 2)] W_{N}^{n}} W_{N / 2}^{n r} \\ = D F T_{N / 2} ((x (n) - x (n + N / 2)) W_{N}^{n}) \end{aligned}

按以上方法反复的分解 N 点 DFT 成 2/N 点 DFT 直到 N=2，使得 N 点傅立叶变换的运算复杂度由
原来的 N2降到 Nlog2N，这是非常显著的改进。这个算法也被称为频域抽取(Decimate-InFrequency, DIF)FFT 算法。。
用一个基2 8 点FFT的图表示上述过程
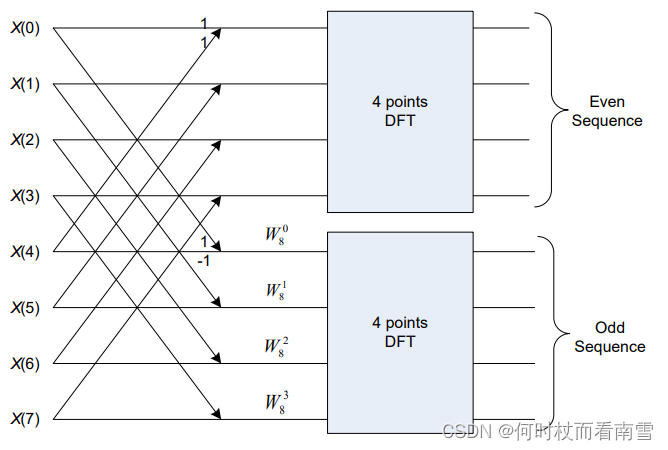
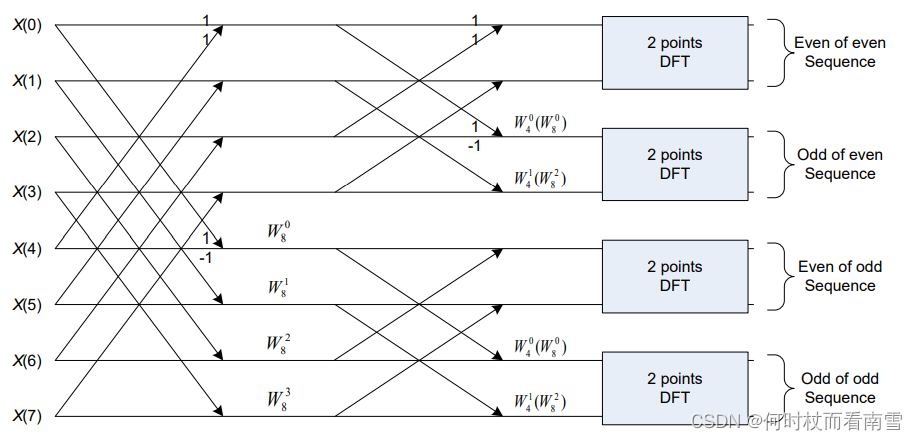
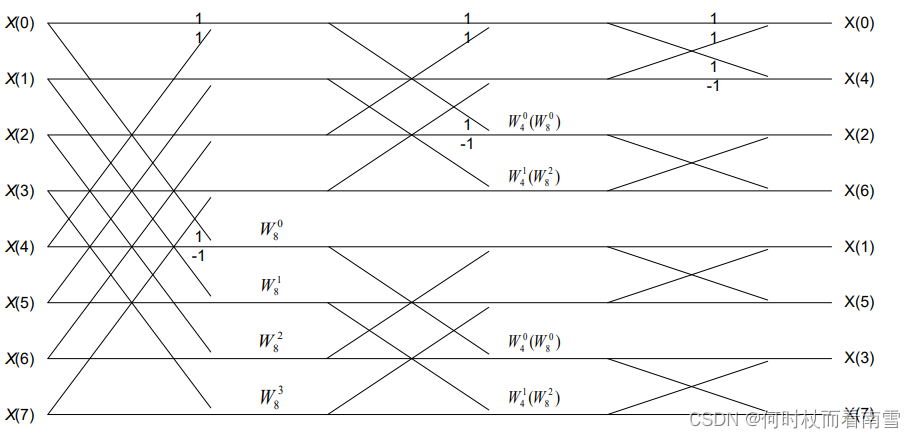
在这里插入图片描述

相关阅读:
算法day38|509,70,746
深入网络底层，了解Linux系统收发网络数据包的过程、原理、流程，附图文说明
Learning with Mini-Batch
三农数据（1990-2020）七：农村居民家庭生产现金支出、农村固定资产构成、固定资产投向
前端使用github pages 部署自己的网站
Leetcode刷题详解—— 找出所有子集的异或总和再求和
docker
Android 从带有html标签的String字符串中提取网页链接url
C/C++内存管理(malloc/calloc/realloc/free/new/delete/operator new/operator delete)
2. MongoDB 应用与开发-安装

原文地址：https://blog.csdn.net/qq_41861711/article/details/127759988