LeetCode——Weekly Contest 319

LeetCode周赛第319场记录
这场周赛的质量也很高，有很多值得学习的地方。

2469. 温度转换

这道题很简单，直接根据已有的信息转换即可，一行代码搞定，注意公式不要敲错。

class Solution {
public:
    vector<double> convertTemperature(double celsius) {
        return {celsius + 273.15, celsius * 1.80 + 32.00};
    }
};
1
2
3
4
5
6

2470. 最小公倍数为 K 的子数组数目

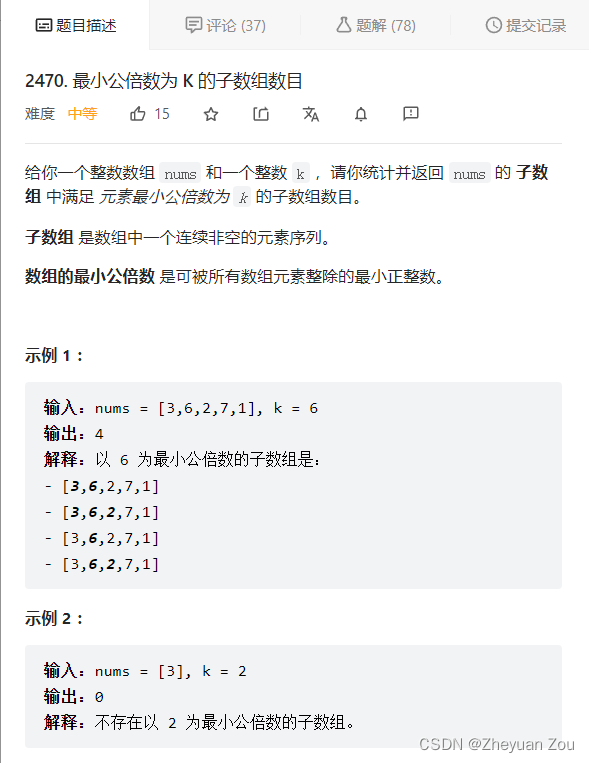
首先这道题要的是最小公倍数，要完成这一点必须了解最小公倍数的求法：

最小公倍数的求解依赖于求最大公约数，记住这个结论。
求解最大公约数的递归算法如下：

int gcd(int a, int b)		// 求最大公约数的递归函数
{
	if(b == 0) 
		return a;
	else return gcd(b, a % b);
}
1
2
3
4
5
6

利用上面这个函数可以快捷地求出a和b的最小公倍数lcm(a,b)：

lcm(a,b) = a / gcd(a,b) * b;
1

给出这道题的完整代码和注释：

class Solution {
	int gcd(int a, int b)					// 求最大公约数的递归函数
	{
		if(b == 0) 
			return a;
		else return gcd(b, a % b);
	}
	
	
public:
    int subarrayLCM(vector<int>& nums, int k) {
        int n = nums.size();
		
		int Ans = 0;
		for(int i = 0 ; i < n ; ++i)
		{
			if(k % nums[i] == 0)
			{
				int Tmp = nums[i];	// 记录当前子数组（滑动窗口）的最小公倍数为nums[i]
				int j = i;			// 以i为左边界开始滑动窗口[i,j]
				while(j < n)
				{
					/*计算当前窗口内所有数的最小公倍数*/
					Tmp = Tmp / gcd(Tmp, nums[j]) * nums[j];
					if(Tmp == k) // 如果当前最小公倍数为k，那么这就是一个答案
						++Ans;
					/*
					如果当前最小公倍数不为k，不能说明它不是一个答案，随着窗口的滑动
					可能在后续出现答案，但是当前最小公倍数和k的最小公倍数不能超过k(可以等于k)
					否则就应该终止循环了
					*/
					if(Tmp / gcd(Tmp, k) * k  == k)	 
						++j;
					else break;
				}
			}
		}
		
		return Ans;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41

2471. 逐层排序二叉树所需的最少操作数目

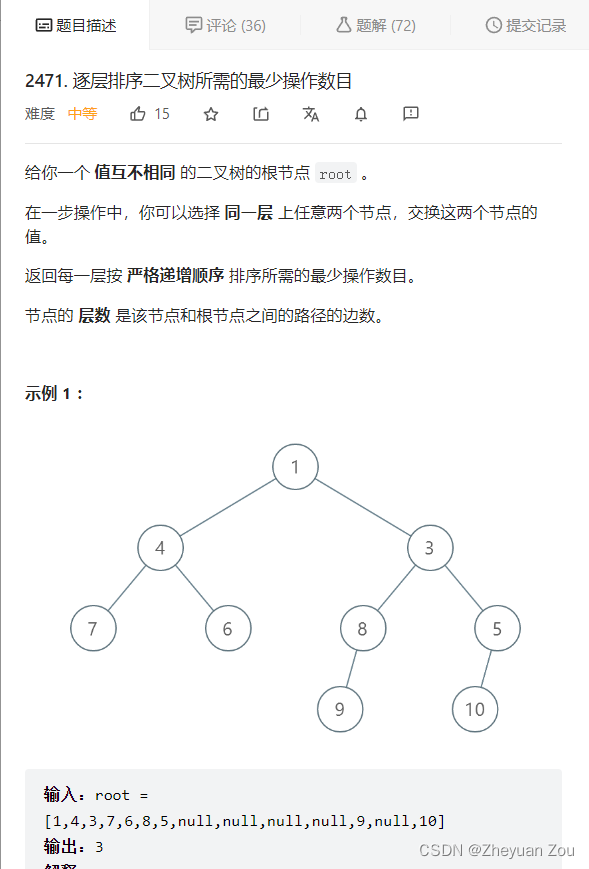
这道题的要求非常的简单易懂，就是给一棵二叉树，按照层序遍历的方式遍历之。每一层只允许通过交换(swap)的方式进行排序，问这样对二叉树逐层进行排序，总共需要多少次交换次数。

对二叉树进行层序遍历是基本算法，这里不再赘述。最困难的地方是解决如下问题：

对于一个指定序列，需要至少多少次交换操作才可以让它有序

这个问题的解法是这样的，首先可以证明这个问题一定是有解的，因为冒泡排序就是通过相邻元素的交换完成的，但是冒泡排序往往不是最优解，它的解法应该如下：

给定一个乱序的序列，比如[4,3,1,2,6]，首先使用sort排序将其按照增量排序为[1,2,3,4,6]。
使用一个哈希表记录每个元素应在的位置，因为本例比较简单，哈希表内容应该如下：

HashTable[1] = 0
HashTable[2] = 1
HashTable[3] = 2
HashTable[4] = 3
HashTable[6] = 4
1
2
3
4
5

然后回到原始序列[4,3,1,2,6]中，从第一个元素4开始：
交换1：按照哈希表指示，4应该在下标为3的地方，交换之得到序列[2,3,1,4,6]
交换2：2应该在下标为1的地方，交换之得到[3,2,1,4,6]
交换3: 3应该在下标为2的地方，交换之得到[1,2,3,4,6]
此时1到达了它应在的地方，交换应该到此结束。

我们逐层使用上述方法对每一层的序列进行排序，加和即可得到最后的结果。
完整的代码如下：

class Solution 
{
public:
    int minimumOperations(TreeNode* root) 
    {
        queue<TreeNode*> Q;
		Q.push(root);
        vector<vector<int>> LayerArray;
		int Ans = 0;
		/*
			对树进行层序遍历来获得每一层的序列
		*/
		while(!Q.empty())
		{
			vector<int> Array{};
			int n = Q.size();
			for(int i = 0 ; i < n ; ++i)
			{
				TreeNode* Front = Q.front();
                Q.pop();
				Array.push_back(Front->val);
				if(Front->left)
					Q.push(Front->left);
				if(Front->right)
					Q.push(Front->right);
			}
            LayerArray.push_back(Array);
		}
		
		/*对每一层的序列执行上述的交换算法，循环计数*/
        for(vector<int>& EachArray : LayerArray)
        {
            int n  = EachArray.size();
            vector<int> Sorted(EachArray.begin(), EachArray.end());
            sort(Sorted.begin(), Sorted.end());
            unordered_map<int, int> Map;
            for(int i = 0 ; i < n ; ++i)
                Map[Sorted[i]] = i;					// 记录数字应该放在什么位置
            for(int i = 0 ; i < n ; ++i)
            {
				/*
				如果当前数字所处位置不是它所在位置，
				交换它和它所应该在的位置上的元素，同时交换操作计数值+1
				*/
                while(EachArray[i] != Sorted[i])	
                {
                    swap(EachArray[i], EachArray[Map[EachArray[i]]]);
                    Ans++;
                }
            }
        }
		return Ans;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54

2472. 不重叠回文子字符串的最大数目

最后一题是一个线性DP，涉及回文子串的问题有两种基本算法要掌握：
1.中心扩展法，时间复杂度$O(n^2)$，空间复杂度$O(1)$。
2.Manacher’s Algorithm(马拉车算法)，时间复杂度和空间复杂度都是$O(n)$。
这两种算法的解释可以见回文子串问题
这道题使用中心扩展法+DP即可，直接给出代码：

class Solution {
public:
    int maxPalindromes(string s, int k) 
    {
    	// f[i]表示下标直到i-1的字符串中满足条件的回文子串个数
        int n = s.length(), f[n + 1];	
        memset(f, 0, sizeof(f));
        for (int i = 0; i < 2 * n - 1; ++i) 
        {
            int l = i / 2, r = l + i % 2; 	// 中心扩展法的合并写法
            f[l + 1] = max(f[l + 1], f[l]);	// 不选择下标为l的字符的情况
            for (; l >= 0 && r < n && s[l] == s[r]; --l, ++r)	// 开始扩展直到形成一个符合要求的字符串
                if (r - l + 1 >= k) 
                {
                    f[r + 1] = max(f[r + 1], f[l] + 1);
                    break;
                }
        }
        return f[n];
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21