-
数组:矩阵快速转置 矩阵相加 三元组顺序表/三元矩阵 随机生成稀疏矩阵 压缩矩阵【C语言,数据结构】(内含源代码)
目录
题目:
稀疏矩阵A,B均采用三元组顺序表表示,验证实现矩阵A快速转置算法,并设计、验证矩阵A、B相加得到矩阵C的算法。
题目分析:
1.从键盘输入矩阵的行数、列数,随机生成稀疏矩阵。
2.生成矩阵A、B后需先转换成三元顺序表,然后用三元顺序表来进行之后的操作。
3.在三元顺序表的基础上使用快速转置(非二维矩阵)。
4.得到三元矩阵相加的结果C。
5.不仅需要输出三元矩阵,还需要把结果转换成二维矩阵输出,以便题目观察结果。
6.程序执行的命令包括:(1)根据输入构造二维矩阵 (2)根据二维矩阵转换成相应的三元矩阵 (3)根据三元矩阵转换为相应的二维矩阵 (4)输出程序 (5)三元矩阵相加 (6)三元矩阵快速转置
7.测试用例:
- 1
- (内置测试用例测试,主要包括相加为0的矩阵测试)
- 2
- 5 5
- 5 5
- (测试5*5和5*5的矩阵)
- 2
- 8 9
- 9 8
- (两个矩阵大小不同,不能进行相加运算,应该有相应的报错)
- 2
- 9 8
- 9 8
- (正常的矩阵测试)
概要设计:
二维矩阵数据结构:

如图,把这种数据结构可视化就是这样的,完全是按照人类习惯的一种存储方式 <( ̄ˇ ̄)/
- typedef struct {
- Elemtype **D;
- int m, n;
- int tu;
- } SparseMatrix, M;
老师说:数据结构决定算法。所以在这里在二维矩阵数据结构中增加行数m、列数n,就可以在进入函数,传参的时候少传入n和m两个值。
tu记录矩阵中非0元素的个数,可以更方便地进行三元数组的转换。
三元数组\三元顺序表顺序表结构:

把上面的二维矩阵转换一下,对应的三元矩阵就长这样,只存了非0元的行、列和数据 ̄へ ̄
三元数据结构的主要作用是将存储信息密度低的二维矩阵,以一种密度更高的方式储存在计算机中。
- typedef struct {
- int i, j;
- Elemtype e;
- } Triple;
- typedef struct {
- Triple data[MAXSIZE + 1];
- int mu, nu, tu;
- } TSMatrix;
首先三元数组数据结构中,三元数组的定义,首先要定义“三元”。
三元Triple 由数据的行i,列j,数据e组成。
三元数组数据结构中同样存储着行数mu,列数nu,非零元个数tu。
详细设计:
三元矩阵相加:
首先,在矩阵相加中有许多操作相同的代码,为了降低代码复用性,所以提取代码中用图相同的代码,做成GO函数当当~ O(∩_∩)O~~
其次,因为大小不同的矩阵不能相加,所以在函数里,可以不用判断两个矩阵的大小,就默认两个矩阵是一样大的。别问我为什么还有注释掉的判断 ╥﹏╥...
最后是最重要的,两个数相加,如果两个答案为0,则不存入,因为他已经成为零元惹(。﹏。*)
然后是相加部分的判断。当两个元素是相同位置的时候,两个执行相加操作,当A的元素在B的后面的时候,则执行前面的B的输入。相反也同理。注意:这里的位置并不是在三元顺序表中的位置,而是在二维数组中的位置,所以不仅可以通过我这种i和j的判断,还可以通过A.data[i][j]-A.data[0][0]得到在数组中的第几位,这种更高级的判断,为什么我没有用捏,因为老师要检查代码,为了更高的阅读性,我选择用传统的i和j的方式( *︾▽︾)
- Status GO(int *t, int *q, TSMatrix A, TSMatrix *C) {
- C->data[*q].i = A.data[*t].i;
- C->data[*q].j = A.data[*t].j;
- C->data[*q].e = A.data[*t].e;
- (*q)++, (*t)++;
- return OK;
- }
- Status AddTripleSMatrix(TSMatrix A, TSMatrix B, TSMatrix *C) {
- //add two tripleM
- int ta = 0, tb = 0, q = 0, tool;
- C->mu = A.mu;
- C->nu = A.nu;
- // if(B.mu > C->mu) {
- // C->mu = B.mu;
- // }
- // if(B.nu > C->nu) {
- // C->nu = B.nu;
- // }
- while(ta < A.tu && tb < B.tu) {
- if(A.data[ta].i == B.data[tb].i) {
- if(A.data[ta].j == B.data[tb].j) {
- tool = A.data[ta].e+B.data[tb].e;
- if(C->data[q].e != 0) {
- C->data[q].i = A.data[ta].i;
- C->data[q].j = A.data[ta].j;
- C->data[q].e = A.data[ta].e+B.data[tb].e;
- q++;
- }
- ta++, tb++;
- } else if(A.data[ta].j > B.data[tb].j) {
- GO(&tb, &q, B, C);
- } else if(A.data[ta].j < B.data[tb].j) {
- GO(&ta, &q, A, C);
- }
- } else if(A.data[ta].i > B.data[tb].i) {
- GO(&tb, &q, B, C);
- } else if(A.data[ta].i < B.data[tb].i) {
- GO(&ta, &q, A, C);
- }
- }
- while(ta < A.tu) {
- GO(&ta, &q, A, C);
- }
- while(tb < B.tu) {
- GO(&tb, &q, B, C);
- }
- C->tu = q;
- return OK;
- }
三元矩阵快速转置:
首先转置有个要求,三元矩阵转置后i要求从小到大排列,所以并不是简单的i = j,j = i就行了。
快速转置前,先看普通转置,知道为什么快速

这是普通转置,可以看到,就是简单的暴力搜索,用了双重循环,时间是N^2,n的平方。为了降低时间复杂度,所以有了快速转置:( ˇˍˇ )
这个呢就是书上的算法,直接上书上的原图吧。

这里讲的是什么意思呢,大致说人话就是:
用num数组存储转置后每一行有多少个数(非零元),用num数组是为了快速求出cpot数组
cpot数组存储转置后每一行第一个元素在三元表里的位置。( ‵▽′)ψ
然后再根据cpot数组,把每个元素送到三元表里对应的地方。
这样说不好理解,举个例子吧┗|*`0′*|┛ :


这个矩阵二维和三元长这样,转置前。
现在先处理num数组,我就遍历三元组j这一列,num数组一开始里面全是0,遍历的时候num[j]++,这样num[j]存的就是(转置前第j列)转置后第i行的非零元数量。
比如第一个j = 2,那么num[2]++;就代表j = 2行多一个数。
第二步,确定cpot数组,
cpot[0] = 0;
for(col = 1; col < Mx.nu; col++) {
cpot[col] = num[col - 1] + cpot[col - 1];
}是的,简单的运算就行就这么简单。
第三步,根据cpot数组,把对应的元素送到合适的地方,让转置后i能从小到大排列。
具体做法是:从上到下,遍历j ,遍历到的第一个j 就是j 列的第一个数【暂停,想一下为什么就是第一个】(⊙3⊙)
以此类推第二个j 就是 j列的第二个。
举例,第一个j = 2是第一个,那么根据cpot数组能确定,j = 2,在转置后是三元组里的第几个元。当我扫描到下一个j = 2的时候,就是转置后j = 2 的第二个元。(⊙ω⊙)

以下是实现
- Status TransposeSMatrix(TSMatrix Mx, TSMatrix *T) {
- //TransposeSM normally
- int col, num[Mx.nu], cpot[Mx.nu], t, p, q;
- T->mu = Mx.nu;
- T->nu = Mx.mu;
- T->tu = Mx.tu;
- if(T->tu) {
- for(col = 0; col < Mx.nu; col++) {
- num[col] = 0;
- }
- for(t = 0; t < Mx.tu; t++) {
- num[Mx.data[t].j]++;
- }
- cpot[0] = 0;
- for(col = 1; col < Mx.nu; col++) {
- cpot[col] = num[col - 1] + cpot[col - 1];
- }
- for(p = 0; p < Mx.tu; p++) {
- col = Mx.data[p].j;
- q = cpot[col];
- T->data[q].i = Mx.data[p].j;
- T->data[q].j = Mx.data[p].i;
- T->data[q].e = Mx.data[p].e;
- cpot[col]++;
- }
- }
- return OK;
- }
调试分析:
1.数组为了我们计算方便,我们是从0开始存的,但是为了我们看起来更符合数学逻辑,更美观,我们要输出i+1,这样输出就是从1开始的。
2.其他就没什么嗦的了,O__O "…
用户手册:
dos操作系统
先选择模式,输入1为测试模式,测试用例会包含所有特殊情况,可以看到结果都能正确处理。
输入2为正常模式,根据提示,输入两个矩阵的长和宽。
1和2模式都会输出原矩阵A,B和他的三元矩阵。AB相加得到的矩阵C和C的三元矩阵。A转置得到的矩阵TA和TA的三元矩阵。
若2模式下,两矩阵A、B大小不同,则无法进行相加操作,输出数组不等大的报错。
测试结果:
输入:
1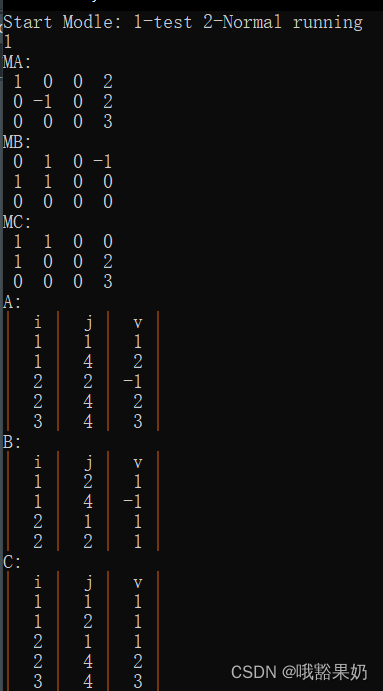

输入:
- 2
- 8 9
- 9 8
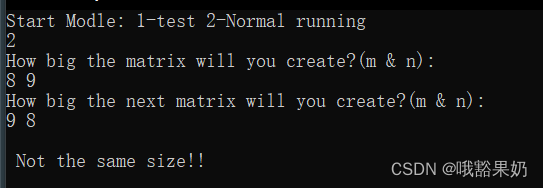
输入:
- 2
- 5 5
- 5 5


这里B的随机结果为0个非零元,比较特殊。
输入:
- 2
- 8 9
- 8 9


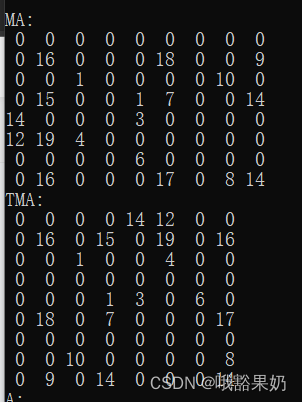
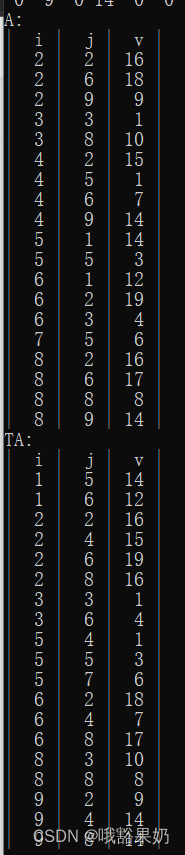
源代码:
主程序:
- #include
- #include
- #include
- typedef int Status;
- #define OK 1
- #define ERROR 0
- typedef int Elemtype;
- #include "Triple.h"
- #include "SparseMatrix.h"
- Status RandInitSM(M *); //scan in m & n ,and Random init a sparseMatrix
- Status TranslateToTM(M, TSMatrix *); //translate M to TM;
- Status TranslateToM(TSMatrix, M *); //translate TM to M;
- Status TransposeSMatrix(TSMatrix, TSMatrix *); //TransposeSM normally
- Status AddTripleSMatrix(TSMatrix, TSMatrix, TSMatrix *); //add two tripleM
- Status TestInit(M *, M *); //test init;
- int main() {
- M MB, MA, MC, TMA;
- TSMatrix A, B, C, TA;
- int chiose = 0;
- printf("Start Modle: 1-test 2-Normal running\n");
- scanf("%d", &chiose);
- if(chiose == 1) {
- TestInit(&MA, &MB);
- } else if(chiose == 2) {
- //Create a Sparsematrix;
- printf("How big the matrix will you create?(m & n):\n");
- RandInitSM(&MA);
- printf("How big the next matrix will you create?(m & n):\n");
- RandInitSM(&MB);
- } else {
- printf("\n ERROR!!\n");
- return 0;
- }
- if(MA.m != MB.m || MA.n != MB.n) {
- printf("\n Not the same size!!\n");
- return 0;
- }
- //Make M to TM;
- TranslateToTM(MA, &A);
- //Make M to TM;
- TranslateToTM(MB, &B);
- //transposeSMatrix
- TransposeSMatrix(A, &TA);
- TranslateToM(TA, &TMA);
- //C = A+B;
- AddTripleSMatrix(A, B, &C);
- //Make TM to M;
- TranslateToM(C, &MC);
- printf("MA:");
- PrintSMatrix(MA);
- printf("MB:");
- PrintSMatrix(MB);
- printf("MC:");
- PrintSMatrix(MC);
- printf("A:\n");
- PrintTM(A);
- printf("B:\n");
- PrintTM(B);
- printf("C:\n");
- PrintTM(C);
- printf("\n------------------\n");
- printf("MA:");
- PrintSMatrix(MA);
- printf("TMA:");
- PrintSMatrix(TMA);
- printf("A:\n");
- PrintTM(A);
- printf("TA:\n");
- PrintTM(TA);
- return 0;
- }
- Status TestInit(M *MA, M *MB) {
- //test init;
- InitSMatrix(3, 4, MA);
- InitSMatrix(3, 4, MB);
- // A
- // 1 0 0 2
- // 0 -1 0 2
- // 0 0 0 3
- // B
- // 0 1 0 -1
- // 1 1 0 0
- // 0 0 0 0
- MA->tu = 5;
- MA->D[0][0] = 1;
- MA->D[0][3] = 2;
- MA->D[1][1] = -1;
- MA->D[1][3] = 2;
- MA->D[2][3] = 3;
- MB->tu = 4;
- MB->D[0][1] = 1;
- MB->D[0][3] = -1;
- MB->D[1][0] = 1;
- MB->D[1][1] = 1;
- return 0;
- }
- Status RandInitSM(M *M) {
- //scan in m & n ,and Random init a sparseMatrix
- int m, n;
- int randN;
- int i, j, k;
- srand((unsigned)time(NULL));
- scanf("%d %d", &m, &n);
- InitSMatrix(m, n, M);
- M->tu = rand() % (m + n) * 2;
- for(k = 0; k < M->tu; k++) {
- i = rand() % m;
- j = rand() % n;
- randN = rand() % 20;
- M->D[i][j] = randN;
- }
- return OK;
- }
- Status TranslateToTM(M M, TSMatrix *TM) {
- //translate M to TM;
- int i, j, cot = 0;
- TM->mu = M.m;
- TM->nu = M.n;
- for(i = 0; i < M.m; i++) {
- for(j = 0; j < M.n; j++) {
- if(M.D[i][j] != 0) {
- TM->data[cot].e = M.D[i][j];
- TM->data[cot].i = i;
- TM->data[cot].j = j;
- cot++;
- }
- }
- }
- TM->tu = cot;
- return OK;
- }
- Status TranslateToM(TSMatrix C, M *MC) {
- //translate TM to M;
- int i;
- MC->m = C.mu;
- MC->n = C.nu;
- MC->tu = C.tu;
- InitSMatrix(C.mu, C.nu, MC);
- for(i = 0; i < C.tu; i++) {
- MC->D[C.data[i].i][C.data[i].j] = C.data[i].e;
- }
- return OK;
- }
- Status TransposeSMatrix(TSMatrix Mx, TSMatrix *T) {
- //TransposeSM normally
- int col, num[Mx.nu], cpot[Mx.nu], t, p, q;
- T->mu = Mx.nu;
- T->nu = Mx.mu;
- T->tu = Mx.tu;
- if(T->tu) {
- for(col = 0; col < Mx.nu; col++) {
- num[col] = 0;
- }
- for(t = 0; t < Mx.tu; t++) {
- num[Mx.data[t].j]++;
- }
- cpot[0] = 0;
- for(col = 1; col < Mx.nu; col++) {
- cpot[col] = num[col - 1] + cpot[col - 1];
- }
- for(p = 0; p < Mx.tu; p++) {
- col = Mx.data[p].j;
- q = cpot[col];
- T->data[q].i = Mx.data[p].j;
- T->data[q].j = Mx.data[p].i;
- T->data[q].e = Mx.data[p].e;
- cpot[col]++;
- }
- }
- return OK;
- }
- Status GO(int *t, int *q, TSMatrix A, TSMatrix *C) {
- C->data[*q].i = A.data[*t].i;
- C->data[*q].j = A.data[*t].j;
- C->data[*q].e = A.data[*t].e;
- (*q)++, (*t)++;
- return OK;
- }
- Status AddTripleSMatrix(TSMatrix A, TSMatrix B, TSMatrix *C) {
- //add two tripleM
- int ta = 0, tb = 0, q = 0, tool;
- C->mu = A.mu;
- C->nu = A.nu;
- if(B.mu > C->mu) {
- C->mu = B.mu;
- }
- if(B.nu > C->nu) {
- C->nu = B.nu;
- }
- while(ta < A.tu && tb < B.tu) {
- if(A.data[ta].i == B.data[tb].i) {
- if(A.data[ta].j == B.data[tb].j) {
- tool = A.data[ta].e+B.data[tb].e;
- if(C->data[q].e != 0) {
- C->data[q].i = A.data[ta].i;
- C->data[q].j = A.data[ta].j;
- C->data[q].e = A.data[ta].e+B.data[tb].e;
- q++;
- }
- ta++, tb++;
- } else if(A.data[ta].j > B.data[tb].j) {
- GO(&tb, &q, B, C);
- } else if(A.data[ta].j < B.data[tb].j) {
- GO(&ta, &q, A, C);
- }
- } else if(A.data[ta].i > B.data[tb].i) {
- GO(&tb, &q, B, C);
- } else if(A.data[ta].i < B.data[tb].i) {
- GO(&ta, &q, A, C);
- }
- }
- while(ta < A.tu) {
- GO(&ta, &q, A, C);
- }
- while(tb < B.tu) {
- GO(&tb, &q, B, C);
- }
- C->tu = q;
- return OK;
- }
头文件SparseMatrix.h:
- #include
- typedef struct {
- Elemtype **D;
- int m, n;
- int tu;
- } SparseMatrix, M;
- Status InitSMatrix(int, int, M *); //Init M;
- Status PrintSMatrix(M);
- Status InitSMatrix(int m, int n, M *M) {
- //Init M;
- M->m = m;
- M->n = n;
- M->D = (Elemtype **)malloc(m * sizeof(Elemtype *));
- for ( int i = 0; i < m; i++) {
- M->D[i] = (Elemtype *)malloc(n * sizeof(Elemtype));
- }
- for (int i = 0; i < m; i++) {
- for (int j = 0; j < n; j++) {
- M->D[i][j] = 0;
- }
- }
- if(M->D) {
- return OK;
- }
- return ERROR;
- }
- Status PrintSMatrix(M M) {
- int i, j;
- for(i = 0; i < M.m; i++) {
- printf("\n");
- for(j = 0; j < M.n; j++) {
- printf("%2d ", M.D[i][j]);
- }
- }
- printf("\n");
- return OK;
- }
头文件Triple.h:
- #define MAXSIZE 12500
- typedef struct {
- int i, j;
- Elemtype e;
- } Triple;
- typedef struct {
- Triple data[MAXSIZE + 1];
- int mu, nu, tu;
- } TSMatrix;
- Status PrintTM(TSMatrix);
- Status PrintTM(TSMatrix TM) {
- int i;
- printf("| i | j | v |\n");
- for(i = 0; i < TM.tu; i++) {
- printf("| %2d | %2d | %2d |\n", TM.data[i].i + 1, TM.data[i].j + 1, TM.data[i].e);
- }
- return OK;
- }
总结:
可以看到两个头文件里其实没什么东西,因为上机实验要展示的东西太多了,也就是说这道题其实不好╮(╯﹏╰)╭,就是要硬考你数据结构。
o_O???
加油↖(^ω^)↗ 一起努力。
-
相关阅读:
记录最近两次java内存过高的分析
golang runc NewSockPair
基于yolov5的草莓成熟度检测系统,可进行图像目标检测,也可进行视屏和摄像检测(pytorch框架)【python源码+UI界面+功能源码详解】
【兔子机器人】项目资料汇总及任务流程
嵌入式系统,ARM微处理器特点,ARM体系结构,特征、状态、操作模式等,中断分类,JTAG调试接口
PostgreSQL数据库统计信息——analyze流程对不同表的处理
52、GNT:Is Attention All NeRF Needs?
嵌入式行业有无年龄危机?算不算青春饭?
智能锁控板的主要功能有哪些?如何使用?
电压放大器如何选择型号规格(电压放大器选型标准)
- 原文地址:https://blog.csdn.net/qq_62792553/article/details/127888804
