4-6 最小生成树Prim,Kruskal(贪心)

4.6最小生成树 Prim,Kruskal(贪心)

一、问题描述

设G =(V,E)是无向连通带权图，即一个网络。E中每条边(u,v)的权为 c[u][v]。
如果G的子图G’是一棵包含G的所有顶点的树，则称G’为G的生成树。生成树上各边权的总和称为该生成树的耗费。
在G的所有生成树中，耗费最小的生成树称为G的最小生成树(Minimum Spanning Tree )，简称MST。

二、构造最小生成树的有效算法:Prim算法和Kruskal算法,

两者贪心选择的方式不同，但都利用了最小生成树性质(贪心策略）∶设G=(V,E)是连通带权图，U是V的真子集。如果(u,v)eE，且ueU , veV-U且在所有这样的边中，(u,v)的权c[u][v]最小，那么一定存在G的一棵最小生成树，它以(u,v)为其中一条边。这性质称为MST(最小生成树）性质。

1.Prim算法（选顶点加入集合S)

- 每次选取能到达的最小的边

设G=(V，E)是连通带权图，V={1,2,.n}。构造G的最小生成树的Prim算法的基本思想是∶
（1）首先置S={1}，
（2）然后，只要S是V的真子集，就作如下的贪心选择:选取满足条件i∈S, j∈V-S，且c[i][i]是最小的边，将顶点j添加到S中。
（3）这个过程一直进行到S=V时为止。
在这个过程中选取到的所有边恰好构成G的一棵最小生成树。

2.Kruskal算法(选择连接属于两个不同连通分支的最小边)

- 每次选取最短的且不构成回路的边

（1）首先将G的n个顶点看成n个孤立的连通分支。
（2）所有的边按权从小到大排序。
（3）顺序检查每条边，如果一条边的端点v和w分别是当前2个不同的连通分支T1和T2，用边(v,w)将T1和T2连接成一个连通分支，否则放弃这条边。
（4）该过程一直到只剩一个连通分支时为止(选择了n-1条边为止)。

三、代码

1.Prim算法（选顶点加入集合S)

- 每次选取能到达的最小的边

//最小生成树Prim算法 
/*每次将能到达的最短的边加进去 
closest[j]是j在S中的邻接顶点,
先找出V-S中使c[j][closest[j]](即lowcost[j]) 值最小的顶点j,
然后根据数组closest选取边(j,closest[j]),然后将j添加到S中,
最后对closest和lowcost做修改 
*/
#include
#include
#define INF 0x3f3f3f
using namespace std;
int n,m;//n个顶点，m条边
int c[100][100];
int s[1000];//s[i]=1表示顶点i被挑出来了，在生成树里了 
int closest[1000];//closest[j]是j在S中的邻接顶点
int lowcost[1000];//lowcost[j]就是c[j][closest[j]] 
void Prim(){
	for(int i=2;i<=n;i++){//初始化 
		lowcost[i]=c[1][i];
		closest[i]=1;
		s[i]=0; 
	}
	s[1]=1; 
	for(int i=1;i<n;i++){
		int t=INF;
		int j=1;//从第一个结点开始 
		for(int k=2;k<=n;k++){
			if(lowcost[k]<t && !s[k]){
				t = lowcost[k]; 
				j=k;
			}
		}
		cout<<"("<<closest[j]<<","<<j<<")= "<<lowcost[j]<<endl;
		s[j]=1;
		for(int k=2;k<=n;k++){
			if(c[j][k]<lowcost[k] && !s[k]){
				lowcost[k] = c[j][k];
				closest[k]=j;		
			}
		}
	}
}
int main(){
	cin>>n>>m;
	int i,j;
	int x,y,z;
	for(i=0;i<=n;i++) //初始化 
		for(j=0;j<=n;j++)
			c[i][j]=INF;
	for(i=0;i<m;i++){
		cin>>x>>y>>z;
		c[x][y]=z;
		c[y][x]=z;
	} 
	cout<<"Prim:依次加入的顺序为：\n";	
	Prim();
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58

2.Kruskal算法(选择连接属于两个不同连通分支的最小边)

- 每次选取最短的且不构成回路的边

//最小生成树Kruskal
//每次选图中权值最小的边 
#include
#include
#include
using namespace std;
int n,m;//n个顶点，m条边
int s[1000];//并查集s[i]=1表示顶点i的父结点是1，即i与1在一个集合
struct edge{
	int u,v,w;//顶点u到顶点v的权重是w(无向图) 
}g[1000];
bool comp(edge a,edge b){
	return a.w < b.w;
}
int Init(){
	for(int i=0;i<m;i++){
		s[i]=i;//初始化，现在各自为王，自己就是一个集合
	}
} 
int Find(int x){//查询根结点
	if(s[x]==x)
		return x;
	else{
		s[x]=Find(s[x]);  //顺便把双亲结点也设置为根结点，路径压缩
		return s[x];
	}	
}
void Merge(int x,int y){//合并,把 y 合并到 x 中去，就是把y的双亲结点设为x
	s[Find(y)] = Find(x);
}
void Kruskal(){
	int x,y;
	for(int i=0;i<m;i++){
		x = g[i].u;
		y = g[i].v;
		if(Find(x) != Find(y)){
			cout<<"("<<x<<","<<y<<")= "<<g[i].w<<endl;
			Merge(x,y);
		}
	}
}
int main(){
	cin>>n>>m;
	int i;
	int x,y,z;
	for(i=0;i<m;i++){
		cin>>x>>y>>z;
		g[i].u=x;
		g[i].v=y;
		g[i].w=z;
	} 
	sort(g,g+m,comp);
	Init();
	cout<<"依次加入的顺序为:\n";
	Kruskal();
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57

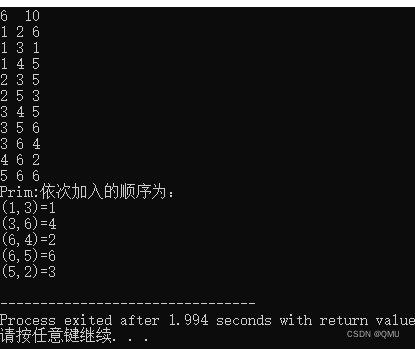
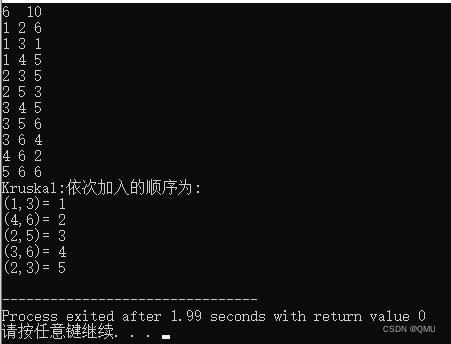
四、运行截图

测试用例

/*
6  10
1 2 6
1 3 1
1 4 5
2 3 5
2 5 3
3 4 5
3 5 6
3 6 4
4 6 2
5 6 6
*/ 
1
2
3
4
5
6
7
8
9
10
11
12
13