KMP算法详解(Python&Java代码）

背景

KMP算法是一种改进的字符串匹配算法，由D.E.Knuth，J.H.Morris和V.R.Pratt提出的，因此人们称它为克努特—莫里斯—普拉特操作（简称KMP算法）。KMP算法的核心是利用匹配失败后的信息，尽量减少模式串与主串的匹配次数以达到快速匹配的目的。具体实现就是通过一个next()函数实现，函数本身包含了模式串的局部匹配信息。KMP算法的时间复杂度O(m+n) [1]  。

算法详解

我们先来看这样一个例子

我们需要在haystack = "121121121121a" 这样的字符串中寻找needle = "121121a"子串，
如果找到了返回第一个匹配到的下标，如果没找到返回-1
这个例子的返回结果是6.

接下来我们以这个为例，详细讲解KMP

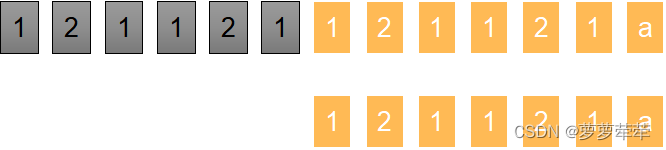
先来暴力方法：

双指针，一个指针指向haystack 的第一个位置，另一个指针指向needle的第一个位置

从开始位置开始逐个进行匹配，相等则指针后移一位

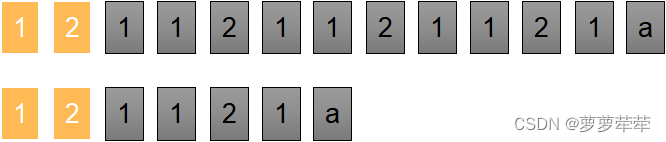
 当不匹配是，指针2回到0位置，指针1的初始点下移一位，开始匹配。

还是匹配不成功，指针2回到0位置，指针1的初始点下移一位，开始匹配。

 

 

 

 首先先了解一个概念，我们需要构建needle字符串对应的一个【最长相同前后缀数组】，这个数组长度与needle（需要寻找的字串）长度一致，每个位置i 的含义是，在needle 的前index-1 的子串的最长相同前缀和后缀的长度。

我们来手动求解下"121121a"的值

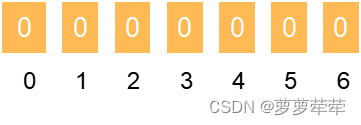
先初始化next数组，使他长度和needle长度一致

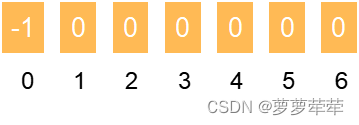
在0位置，0~i-1 的子字符串长度没有，所以0位置的值固定为-1

在1位置，前一个字符为"1", 最大前缀为"1", 最大后缀为”1“，就是它本身，所以不考虑，所以最大相同前后缀为0

 在2位置，前缀字符为”12“， 前后缀是["1", "2"]，不相等所以是0。 

在3位置，前缀字符为"121", 前缀后匹配串有两对， ["1", 1"], ["12", "21"], 所以最大相同前后缀长度为1

后面不加赘述，最终生成的next数组为

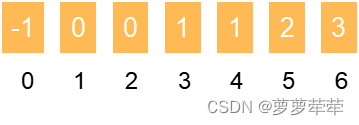
 以上是用暴力方法生成next数组，下面我们来看看如何加速next数组的生成过程

首先next数组的0位置固定为-1， 1位置固定为0，后面计算加速方式是利用前一个位置的信息

下面进行分类讨论

如果前一个位置的长度为c，并且前一个字符和第c个字符是一样的，那么当前位置长度+1

如下图，我们计算指针位置i的值时候，会观察前一个位置i-1，和c位置是否一样，其含义因为【0~c-1】位置一定等于【i-1-c~ i-2】一定是相等的，因为这个上一段计算所得。只需要比较c位置和i-1位置的字符是否一致，如果一致直接在上一段计算结果上+1，如下图所示：

 

如果c位置和i-1位置的字符不一致。则c=next[c] 仍然比较i-1 和c位置的字符是否一致，

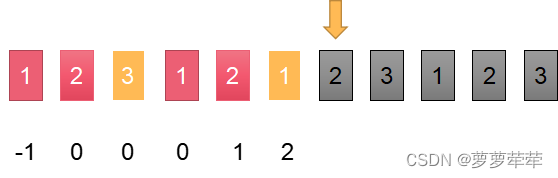
 如图，黄色色块不等，c=next[c]，黄色色块往前移动，这下相等了，计算结果是c+1

 我们再看几个案例熟悉以下这个流程。

 

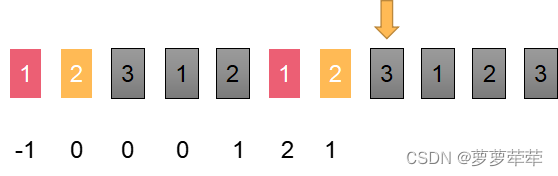
这个位置i-1 位置等于c位置的字符，所以此位置长度为c+1 

 

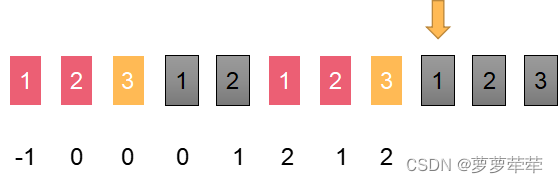
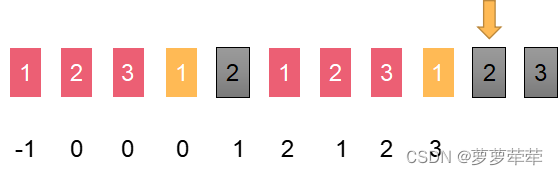
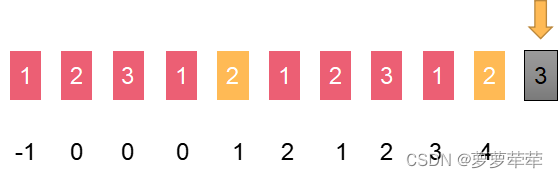
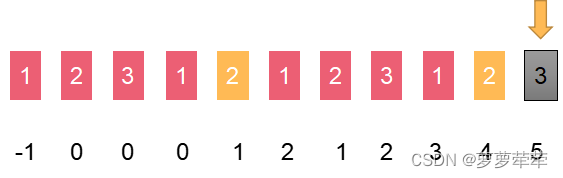
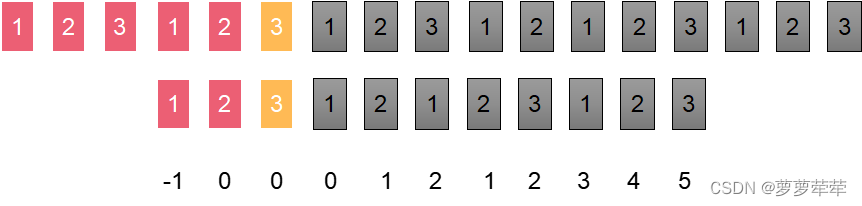
所以[1, 2, 3, 1, 2, 1, 2, 3, 1, 2, 3] 的nexts数组为 【-1，0，0，0，1，2，1，2，3，4，5】

如果要匹配字符串"12312312123123" ，最终结果为

 这个过程我们从头开始实现：

我们设置两个指针分别指向匹配字符串和被匹配字符串的第一个位置。

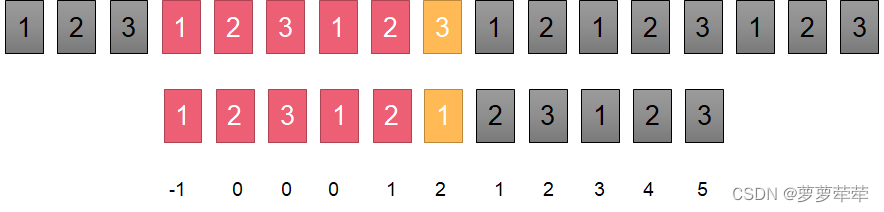
如果两个指针所指的字符相等，则+1，

 

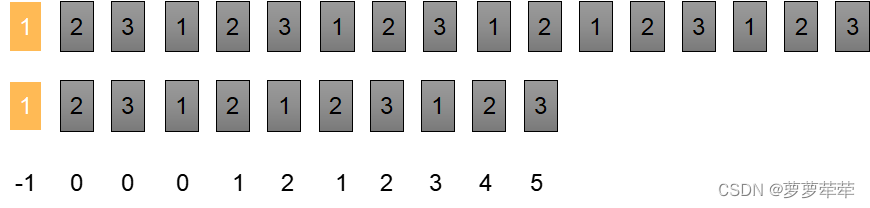
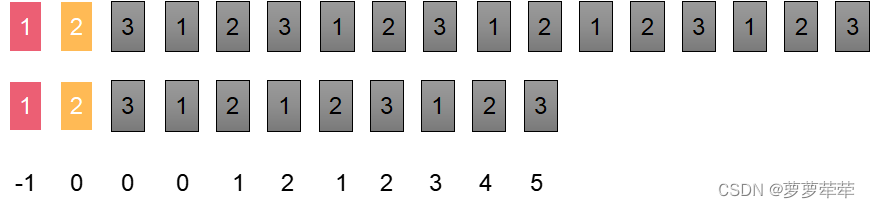
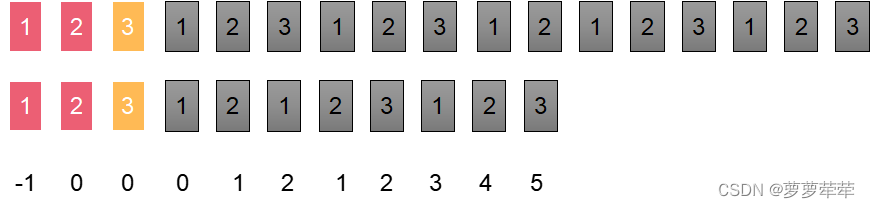
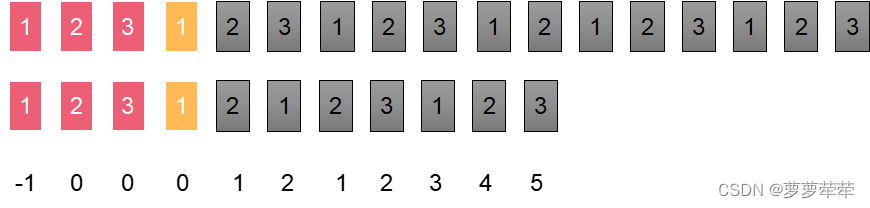
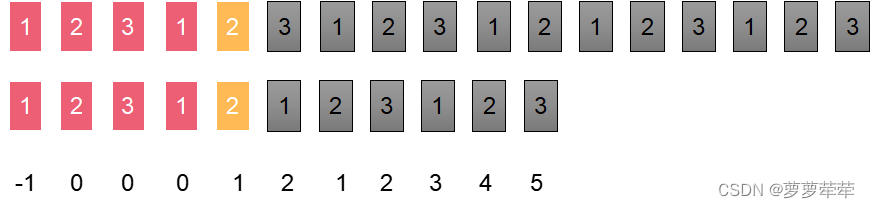
如图说是这时候两指针所指位置字符不相等了， 此时比较i位置字符和nexts[i]位置的字符是否相等。

 

 

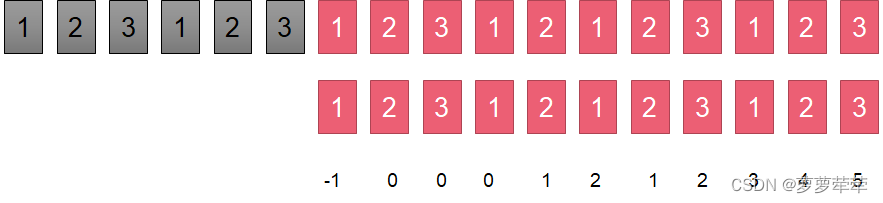
 匹配成功！